In the given figure, ABC is a right-angled triangle with AB=6cm and AC=8cm. A circle with centre O has been inscribed inside the triangle. Calculate the value of r, the radius of the inscribed circle.

Join OA , OB and OC
Draw OD⊥AB, OE⊥BC and OF⊥CA.
Then, OD=OE=OF=rcm.
∴ar(ΔABC)=12×AB×AC=(12×6×8)cm2=24cm2
Now, ar(ΔABC)=12×(perimeter ofΔABC)×r
⇒24=12×(AB+BC+CA)×r
⇒24=12×(6+10+8)×r⇒r=2 [∴BC2=AB2+AC2⇒BC=√62+82=10]
Hence, the radius of the inscribed circle is 2cm.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8A16videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8B15videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)30videos
ARITHMETIC PROGRESSION
- BOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself10videos
CONSTRUCTIONS
Similar Questions
In the given figure ABC is a right angled triangle with AB=6 cm, and BC=8 cm. A circle with centre O has been inscribed inside the triangle. Find the radius of the circle.
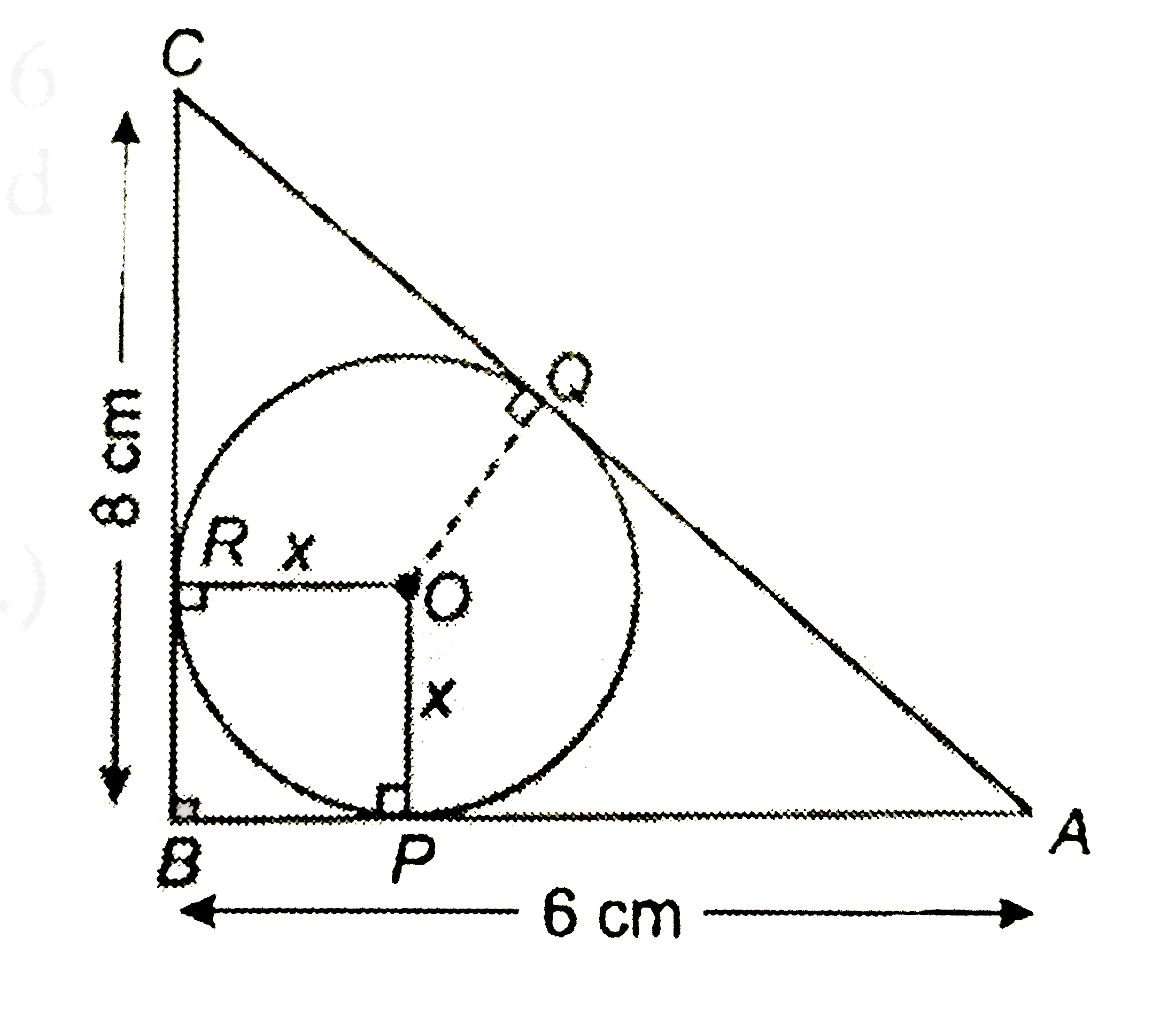 View Solution
View SolutionIn the given figure ΔABC is right angle at A with AB=6 cm and AC=8 cm. A circle with centre O has been inscribed inside the triangle. Find the value of r, the radius of the inscribed circle.
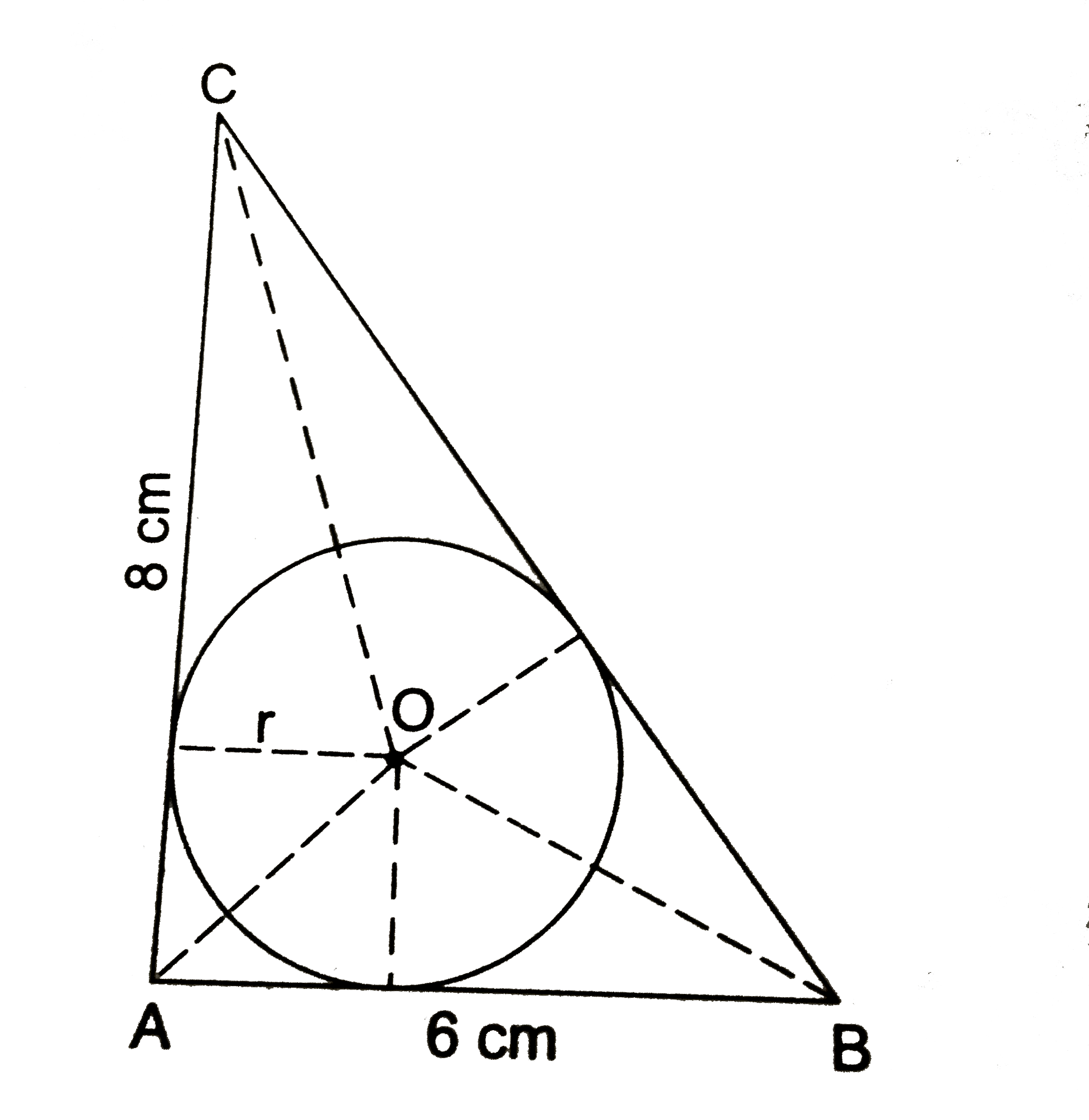 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
ABC is a right-angled triangle with AB = 6 cm and BC = 8 cm. A circle with centre O has been in scribed inside ΔABC. The radius of the circle is
A1 cmB2 cmC3 cmD4 cm - Question 2 - Select One
ΔABC is right angled triangled with AB=6 cm, BC=8cm. O is the in centre of the triangle.The ratius of the in -circle is :
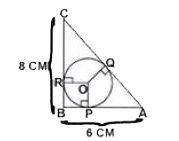 A2cmB5cmC4cmD3cm
A2cmB5cmC4cmD3cm - Question 3 - Select One
ABC is a right angle triangle right angled at A. A circle is inscribed in it the length of the two sidescontaining right angle are 6 cm and 8 cm then the radius of the circle is
A3 cmB2 cmC5 cmD4 cm
PQR is a right angled triangle at Q with QR =12 a=cm and PQ=5cm. A circle with centre O is inscribed in △PQR. Find the radius of the circle.
View SolutionΔABC is a right angled triangle with ∠A=900AB=bcm,AC=acm,andBC=ccmAcircle is inscribed in this triangle. The radius of the circle,in cm, is:
View SolutionIn the given figure,ABC in a right-angled triangle,right-angled atB.IfBC=5cmandAC-AB=1cm,f∈dthevalueofcosecAandcos A
View SolutionIn the given figure, in a right angle triangle ABC, AB=12cm and AC=15cm. A square is inscribed in the triangle. One of the vertices of square coincides with the vertex of triangle. What is the maximum possible area (in cm2) of the square ?
 View Solution
View SolutionABC is a right angle triangle right angled at A. A circle is inscribed in it the length of the two sidescontaining right angle are 6 cm and 8 cm then the radius of the circle is
View Solution

