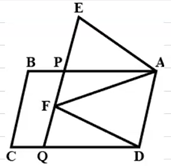
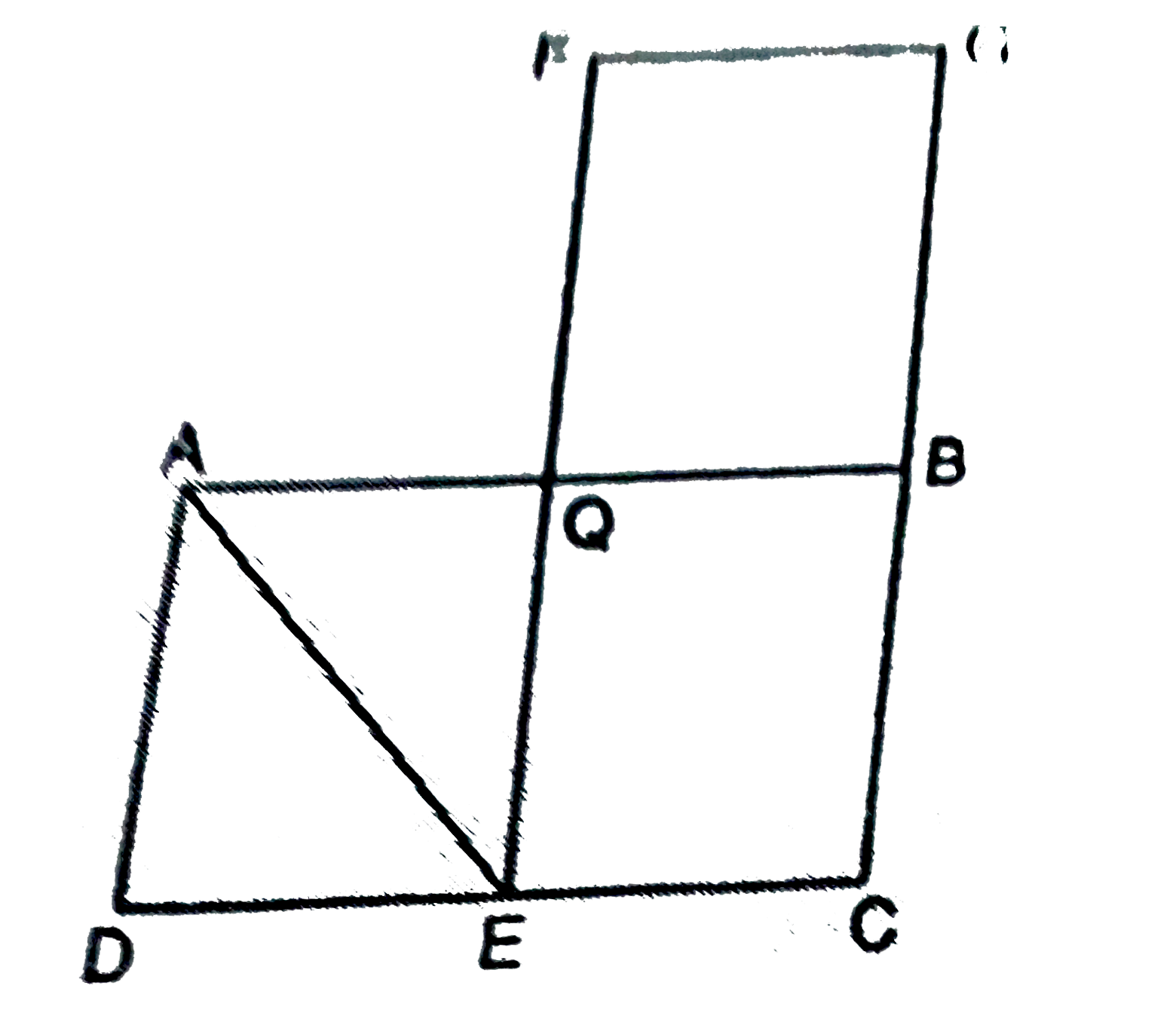
In the given figure, ABCD and AEFD are two parallelograms. Which of the following statements is correct?

I. PE = QF
II ar(ΔAPE)ar(ΔPFA)=ar(ΔQFD)ar(ΔPFD)
III. ar(ΔPEA)=ar(ΔQFD)
Only I
Only I and III
Only II and III
I, II and III
The correct Answer is:D
Step by step video, text & image solution for In the given figure, ABCD and AEFD are two parallelograms. Which of the following statements is correct? I. PE = QF II (ar(Delta APE))/(ar(Delta PFA)) = (ar(Delta QFD))/(ar(Delta PFD)) III. ar(Delta PEA) = ar (Delta QFD) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- IMO QUESTION PAPER SET A 2019BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER SET A 2019EXERCISE - Everyday Mathematics
10 Videos
- IMO QUESTION PAPER SET A 2017BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER SET A 2017EXERCISE - ARCHIEVERS SECTION
5 Videos
- IMO QUESTION PAPER SET B 2019BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER SET B 2019EXERCISE - ACHIEVERS SECTION
5 Videos
Similar Questions
Knowledge Check
In the given figure, ABCD and AEFD a re two parallelograms.
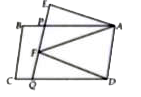
ar(ΔPEA) =Aar(∣∣gmΔPEA)Bar(ΔPFD)Car(ΔQFD)Dar(∣∣gmΔCQPB)In the given figure, ABCD and AEFD a re two parallelograms.
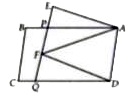
(ar(ΔAPE))/(ar(ΔPFA)) =A(ar(ΔQFD))/(ar(ΔPFD))B(ar(ΔAEF))/(ar(ΔPFD))C(ar(ΔQFD))/(ar(ΔAEF))DNone of these
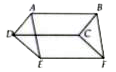
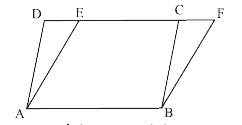
In the figure, ABCD, DCFE and ABFE are parallelograms. Show that ar(ΔADE) = ar(ΔBCF).
View SolutionIn the given figure, ABCD and FECG are parallelograms equal in area. If ar(ΔAQE)=12cm2, find ar(∣∣gmFGBQ)
View SolutionIn the figure ABCD and ABFE are Parallelograms then find ar (ΔBCF).
If ar (ABCE)=18cm2
ar (ABCD)=25cm2
View SolutionIn the given figure, ΔABCandΔDBC are on the same base BC. If AD intersects BC at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
View SolutionIn the figure, ABC and BDE are two equilateral triangle such that D is the mid-point of BC. If AE intersects BC at F, show that:
(i) ar(ΔBDE)=14ar(ΔABC) (ii) ar(ΔBDE)=12ar(ΔBAE)
(iii) ar(ΔABC)=2ar(ΔBEC) (iv) ar(ΔBFE)=ar(ΔAFD)
(v) ar(ΔBFE)=2ar(ΔFED) (vi) ar(ΔFED)=18ar(ΔAFC)

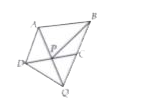
View SolutionIn the figure, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar(ΔBPC) = ar(ΔDPQ).
View Solution