In the figure, ABC and BDE are two equilateral triangle such that D is the mid-point of BC. If AE intersects BC at F, show that:
(i) ar(ΔBDE)=14ar(ΔABC) (ii) ar(ΔBDE)=12ar(ΔBAE)
(iii) ar(ΔABC)=2ar(ΔBEC) (iv) ar(ΔBFE)=ar(ΔAFD)
(v) ar(ΔBFE)=2ar(ΔFED) (vi) ar(ΔFED)=18ar(ΔAFC)

Join EC and AD.
Let a be the side of ΔABC. Then
ar(ΔABC)=a2√34=Δ (say)
(i) ar(ΔBDE)=(a2)2√34=14×a2√34
=14Δ=14ar(ΔABC)...(1)
(ii) Since, DE is the median in ΔBEC,
∴ar(ΔBDE)=12ar(ΔBEC)
(∴ median divides the triangle into two equal parts)...(2)
Now, ∠1=60∘=∠2 (each angle of equilateral triangle)
But these are the alternate angles
∴BE∣∣AC
∴ar(ΔBEC)=ar(ΔBAE)
(∴ triangle are on the same base BE and between same parallel BE and AC) ....(3)
∴ From (2) and (3), we get
ar(ΔBDE)=12ar(ΔBAE)
(iii) Now, ar(ΔBDE)=12ar(ΔBEC) [From (2)]
⇒14ar(ΔABC)=12ar(ΔBEC) [from (1) and (2)]
⇒ar(ΔABC)=2ar(ΔBEC)
(iv) ∠3=∠4=60∘ (each angle of equilateral triangle)
But these are the alternate angle
∴BA∣∣ED
∴ar(ΔBDE)=ar(ΔAED)
(∴ triangles are on the same base DE and between the same parallels DE and AB)
⇒ar(ΔBDE)−ar(ΔFED)=ar(ΔAED)−ar(ΔFED)
⇒ar(ΔBEF)=ar(ΔAFD)...(4)
(v) We know that in an equilateral triangle, median and prependicular are same.
∴AD⊥BC
∴InΔABD, AD2=AB2−BD2 (by Phythagoras theorem)
a2−(a2)2=3a24
∴AD=a√32
In ΔBED, draw EG⊥BD
∴EG2=DE2−DG2
=(a2)2−(a4)2=a24−a216=3a216
∴EG=a√34
∴ar(ΔAFD)=12×FD×AD=12×FD×a√32....(5)
and ar(ΔEFD)=12×FD×EG=12×FD×a√34...(6)
From (5) and (6), we get
ar(ΔAFD)=2ar(ΔEFD)....(7)
∴ From (4) and (7), we get
ar(ΔBEF)=ar(ΔAFD)=2ar(ΔEFD)....(8)
(vi) Since, ar(ΔBDE)=14ar(ΔABC) [from (1)]
⇒ar(ΔBEF)+ar(ΔEFD)=14×2ar(ΔADC)
⇒2ar(ΔFED)+ar(ΔFED)=12[ar(ΔAFC)−ar(ΔAFD)] [from (8)]
⇒3ar(ΔFED)=12ar(ΔAFC)−12×2ar(ΔFED) [from (7)]
∴4ar(ΔFED)=12ar(ΔAFC)
⇒ar(ΔFED)=12ar(ΔAFC)

Topper's Solved these Questions
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Problems From NCERT/exemplar
12 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Exercise
34 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )
5 Videos
Similar Questions
In figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
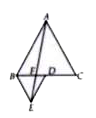
ar(ΔBDE) = 1/4 ar(ΔABC)
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
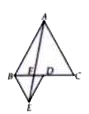
ar(ΔBDE) = 1/2 ar(ΔBAE)
View Solution
Knowledge Check
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=12ar(ΔABC).
ATrueBFalseCPartially trueDNone of these
In figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
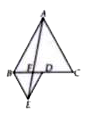
ar(ΔABC) = 2 ar(ΔBEC)
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
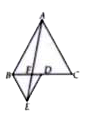
ar(ΔBFE) = 2 ar(ΔFED)
View SolutionIn fig, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that: (i) ar(BDE)= 1/4 ar(ABC) (ii) ar(BDE)= 1/2 ar(BAE)
View SolutionIn the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
(i)ar(△BDE)=14ar(△ABC)
(ii)ar(△BDE)=12ar(△BAE)
(iii)ar(△ABC)=2ar(△BEC)
(iv)ar(△BFE)=ar(△AFD)
(v)ar(△BFE)=2ar(△FED)
(vi)ar(△FED)=18ar(△AFC).

View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=14ar(ΔABC).
View SolutionABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD.
Prove that ar(△BED)=14ar(△ABC).

View SolutionIf the median of a △ABC intersect at G. show that ar (△AGC) = ar (△AGB) = ar (△BGC) = 1/3 ar (△ABC)
View Solution
