In the given figure, ABCD is a rectangle of length 51 cm and bredth 25 cm. A trapezium PQCD with its parallel sides QC and PD in the ratio 9 : 8 is cut off from the rectangle, as shown in the figure. If the area of the trapezium PQCD is 56th part of the area of the rectangle, find the lengths QC and PD.
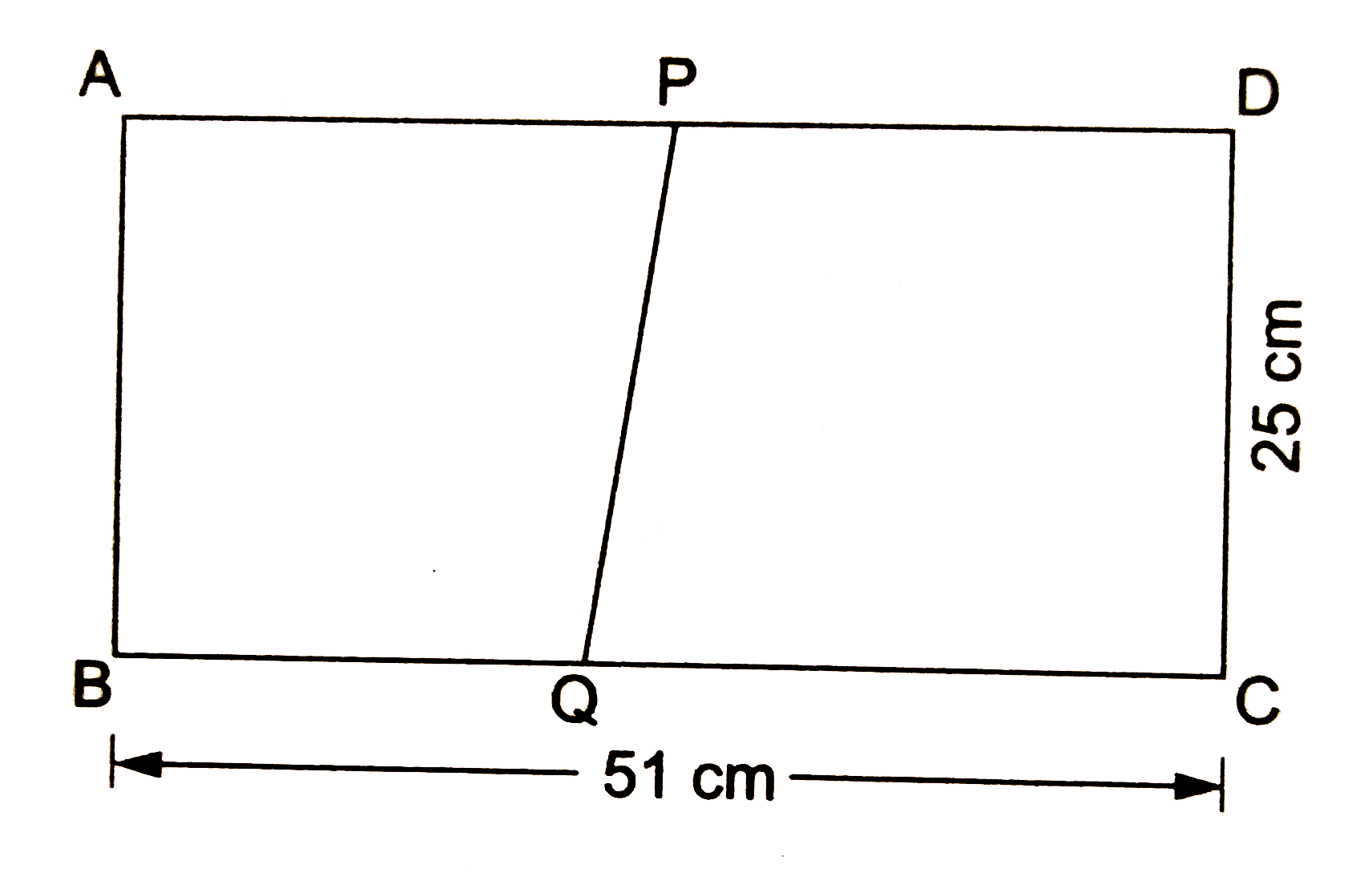
Length of rectangle ABCD = 51 cm.
Breadth of rectangle ABCD = 25 cm.
Area of rectangle ABCD = (51×25)cm2=1275cm2.
Let QC = 9k and PD = 8k. Then,
area(trap. PQCD)
=(12×sum of parallel sides×distance between them)
={12×(9k+8k)×25}cm2=(17×252)k cm2.
Now, area (trap. PQCD) = 56× (area of rectangle ABCD)
⇒ (17×252)k=(56×1275)
⇒ k=(56×1275×217×25)⇒k=5.
∴ QC=(9k)cm=(9×5)cm = 45 cm
and PD = (8k) cm = (8×5)cm = 40 cm.
Hence, QC = 45 cm and PD = 40 cm.
Topper's Solved these Questions
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Exercise 14
32 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - EXERCISE
12 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE
5 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
Similar Questions
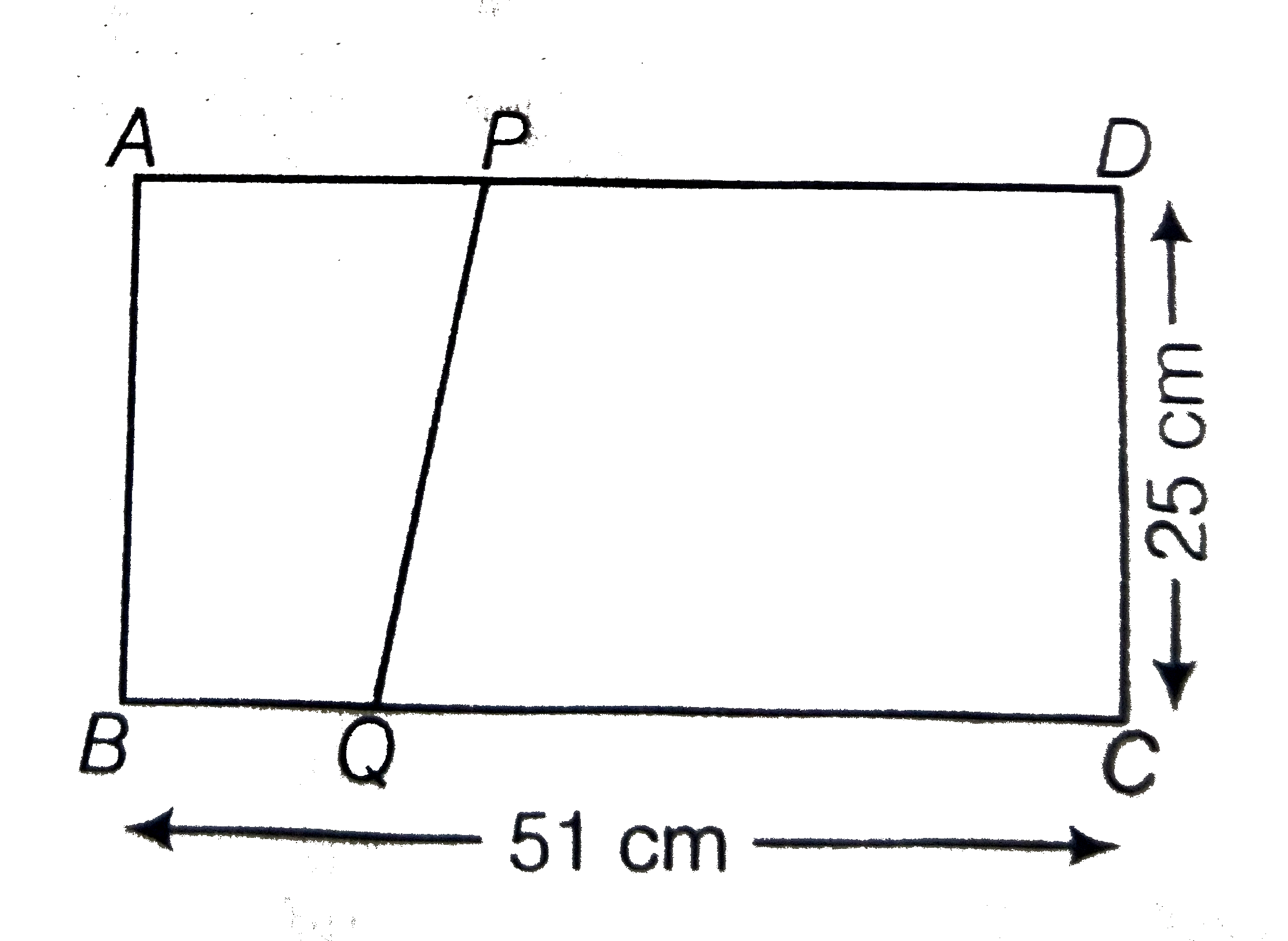
The dimensions of a rectangle ABCD are 51 cm×15 cm.AtrapeziumPQCDwithitsparal≤lssQCandPD∈theratio9:8,iscutoffomtherectang≤asshown∈thefigure.IftheareaofthetrapeziumPQCDis(5)/(6) th part of the area of the rectangle. Find the length QC and PD.
View SolutionFind area and perimeter of rectangle with length 5 cm and breadth 6 cm
View Solution
Knowledge Check
In the given figure , ABCD is a trapezium in which the parallel sides AB,CD are both perpendicular to BC. Find the area of the trapezium :
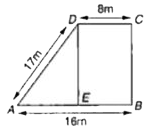 A140m2B168m2C180m2D156.4m2
A140m2B168m2C180m2D156.4m2The parallel sides of a trapezium are in a ratio 2: 3 and their shortest distance is 12 cm. If the area of the trapezium is 480 sq. cm, the longer of the parallel sides is of length
A36 cmB42 cmC48 cmD56 cm
Find the area of rectangle whose length is 6cm and breadth 4cm.
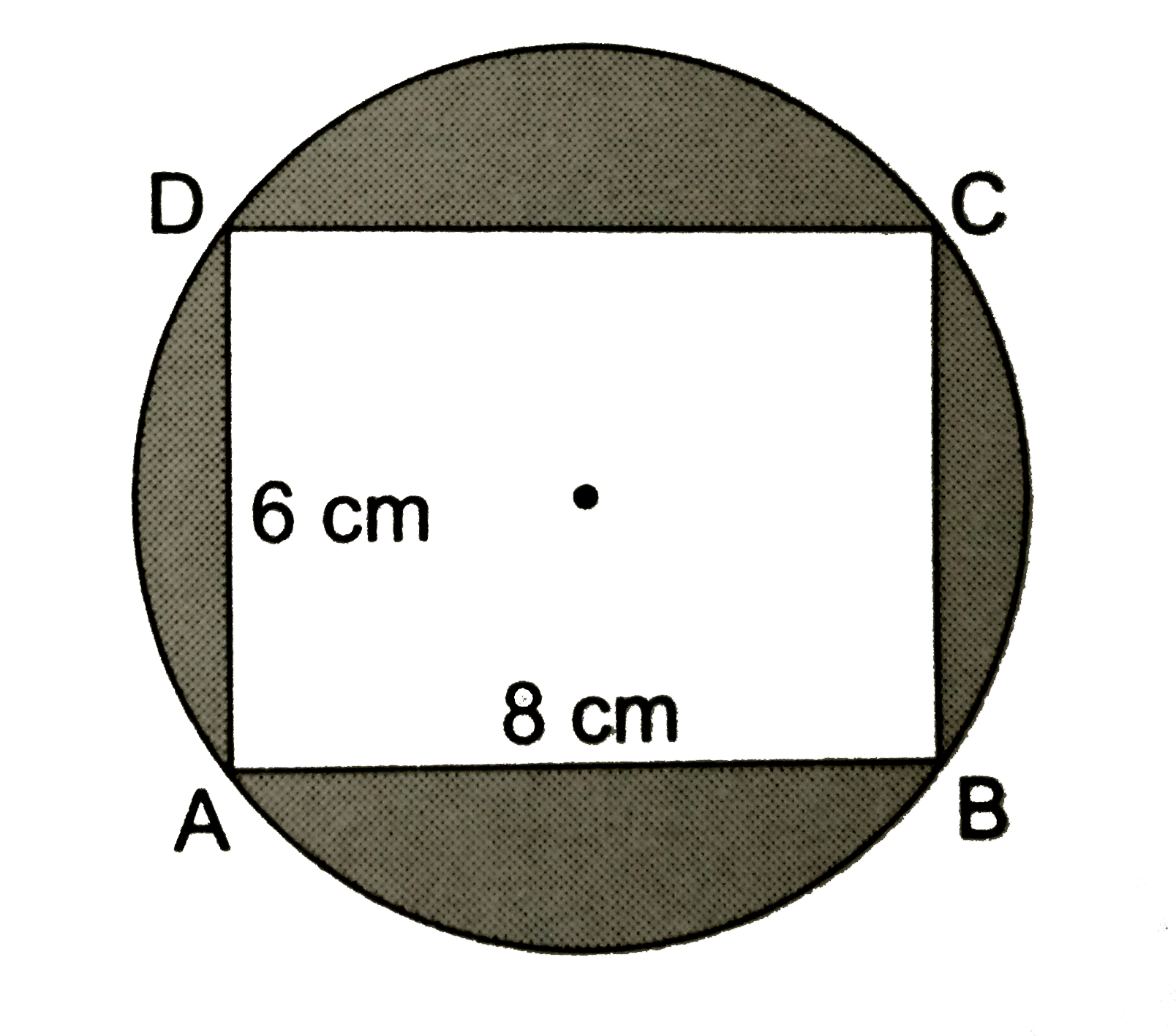
View SolutionIn the given figure ABCD is a rectangle inscribed in a circle having length 8 cm and breadth 6 cm. If π=3.14 then the area of the shaded region is
View SolutionThe lengths of the parallel sides of a trapezium are in the ratio 5:3 and the distance between them is 12 . 5 cm .If the area of the trapezium is 450cm2 , find the lengths of its parallel sides .
View SolutionThe perimeter of a rectangle is 130 cm. If the breadth of the rectangle is30 cm, find its length. Also find the area of the rectangle.
View SolutionThe parallel sides of a trapezium are 12 cm and 9 cm and the distance between them is 8 cm . Find the area of the trapezium.
View SolutionA rectangular' sheet is cut along its length into five equal squares as shown in the figure. The area of a square is 16cm2. Find the perimeter of the rectangle.

View Solution
