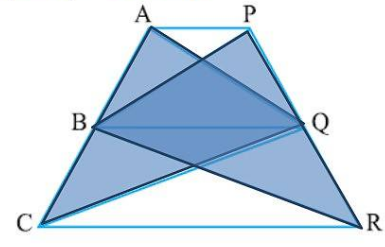
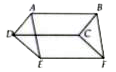
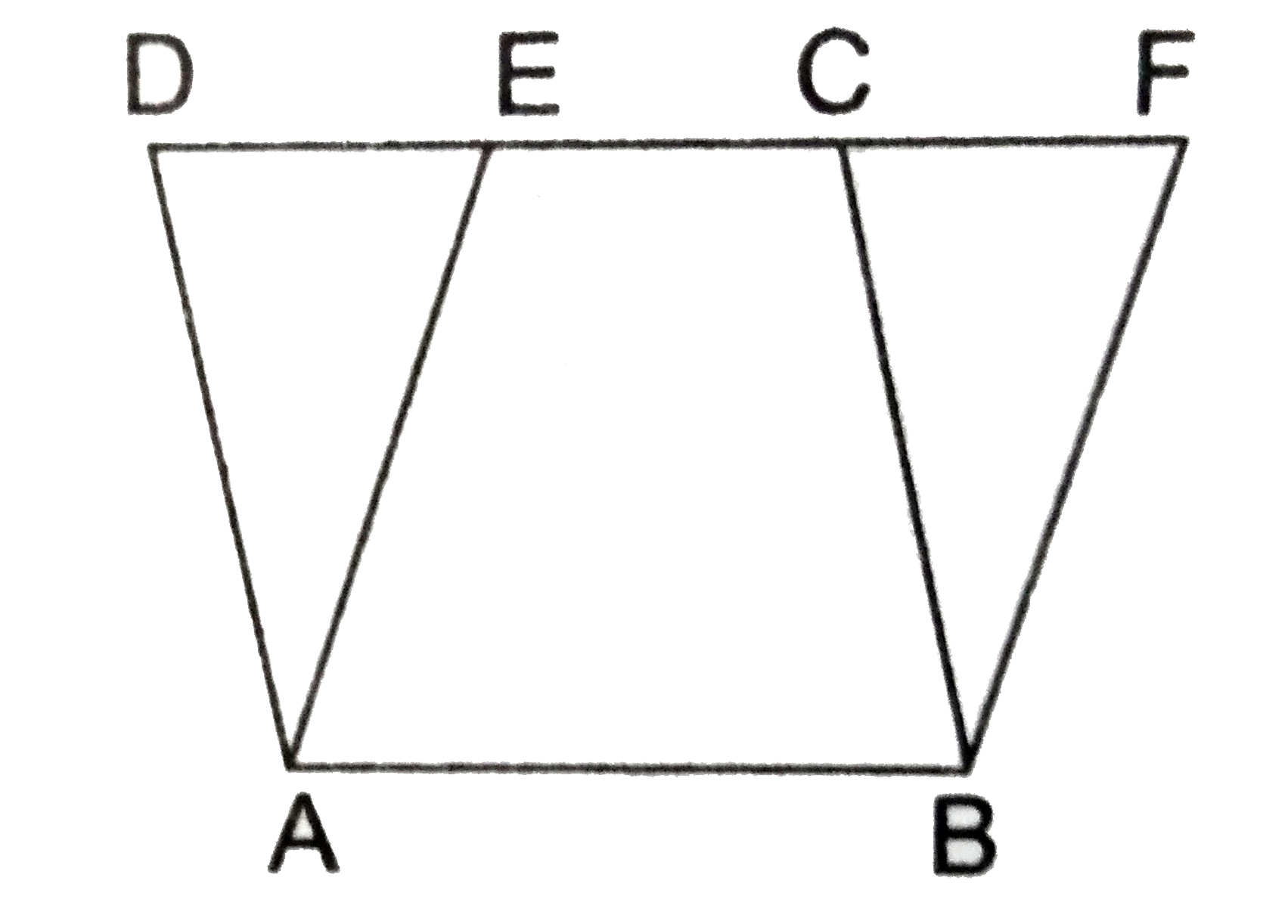
In the given figure , ar (DRC) = ar ( DPC) and ar(BDP) = ar(ARC) . Show that both the quadrillaterals ABCD and DCPR are trapeziums.

Text Solution
The correct Answer is:ABCD is a trapezium
|
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Exercise 11.4
8 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE 11.2
6 Videos
- CIRCLES BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - CIRCLES EXERCISE - EXERCISE 12.6
4 Videos
Similar Questions
Knowledge Check
In the given figure ar (ΔABC)= ar (ΔADE). AC is the median of ΔADE. If ar (ACE) =14cm2 then ar (ΔABC) = ?
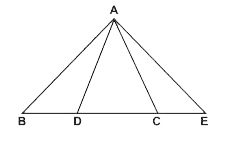 A14cm2B7cm2C21cm2D28cm2
A14cm2B7cm2C21cm2D28cm2In the given figure, ABCD and AEFD a re two parallelograms.
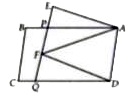
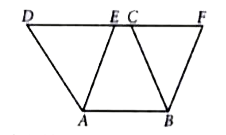
(ar(ΔAPE))/(ar(ΔPFA)) =A(ar(ΔQFD))/(ar(ΔPFD))B(ar(ΔAEF))/(ar(ΔPFD))C(ar(ΔQFD))/(ar(ΔAEF))DNone of theseIn the given figure, ABCD and ABEF are parallelograms such that ar(quad. EABC) 17cm2 and ar(||gm ABCD) =25cm2. Then ar(△BCF) = ?
 A4cm2B4.8cm2C6cm2D8cm2
A4cm2B4.8cm2C6cm2D8cm2
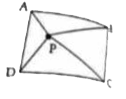
In the figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(△APB)+ar(△PCD=12ar(ABCD)
(ii) ar(△APD)+ar(△PBC)=ar(△APB)+ar(△PCD)

View SolutionIn the adjacent figure P is a point inside the parallelogram ABCD. Prove that
ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
View SolutionIn the given figure, ABCD and ABFE are parallelograms such that ar(quad. EABC) =19 cm2 and ar(||gm ABCD) = 28 cm2. Then, ar(△BCF) is
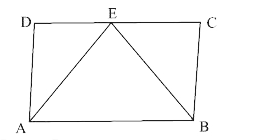
View SolutionIn given figure. If area of parallelogram ABCD is 30cm2 then find ar (ΔADE)+ ar (ΔBCE)
View SolutionIn the given figure, ABCD is a ||gm in which diagonals AC and BD intersect at O. If ar(||gm ABCD) is 52cm2 then the ar(△AOB)=?
View Solution