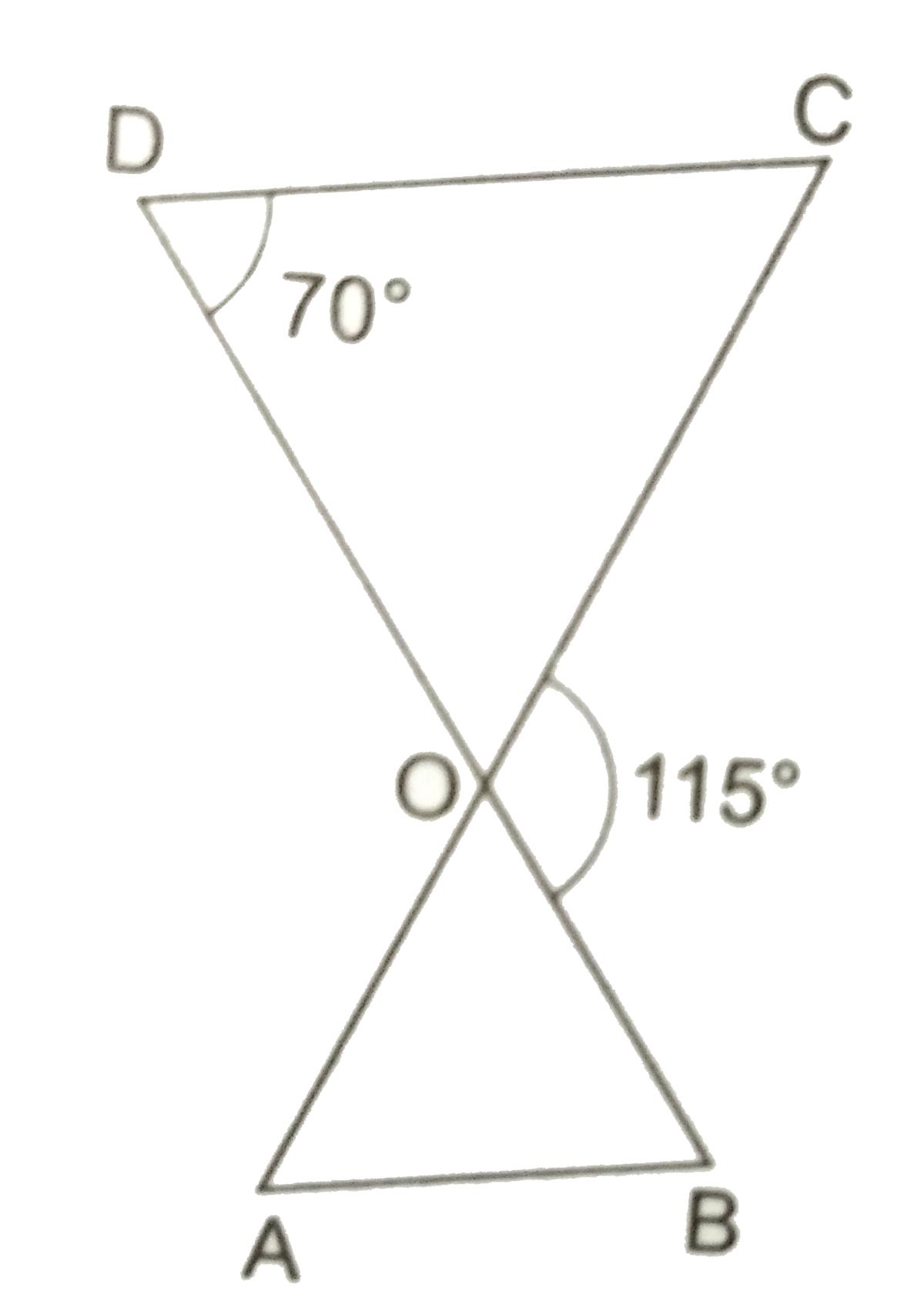In the given figure, ΔOQP~ΔOAB,∠OPQ=56∘and∠BOQ=132∘. Find ∠OAB.
Video Solution
Text Solution
In ΔOPQ, we have
∠BOQ=∠OPQ+∠OQP [ ∴ the exterior angle is equal to the sum of the two interior opposite angles ]
⇒∠OQP=∠BOQ−∠OPQ=132∘=132∘−56∘=76∘,
Now, ΔOQP~ΔOAB
⇒∠OQP=∠OAB [ corresponding angles of similar triangles]
∴∠OAB=∠OQP=76∘
|
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Video
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
Knowledge Check
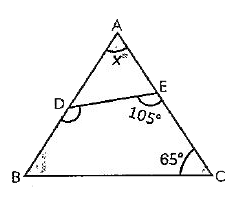
What is the value of x in the given figure, if
ΔADE~ΔACB,∠DEC=105∘ and ∠ECB=65∘
 A45∘B60∘C13∘D40∘
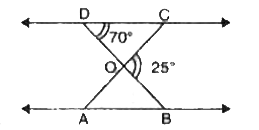
A45∘B60∘C13∘D40∘In the given figure ΔODC~ΔOAB,∠BOC=125∘,∠ODC=70∘, then ∠OAB is equal to :
 A70∘B35∘C50∘D55∘
A70∘B35∘C50∘D55∘ΔACB≅ΔDFE. Find ∠F
 A4∘B96∘C100∘D60∘
A4∘B96∘C100∘D60∘
In a ΔABC∠A+∠B=145∘,2∠B+∠C=180∘ Find ∠Aand∠B
View SolutionSee figure. In ΔABC,∠B90∘,∠A=30∘,AC=14, then find AB and BC.
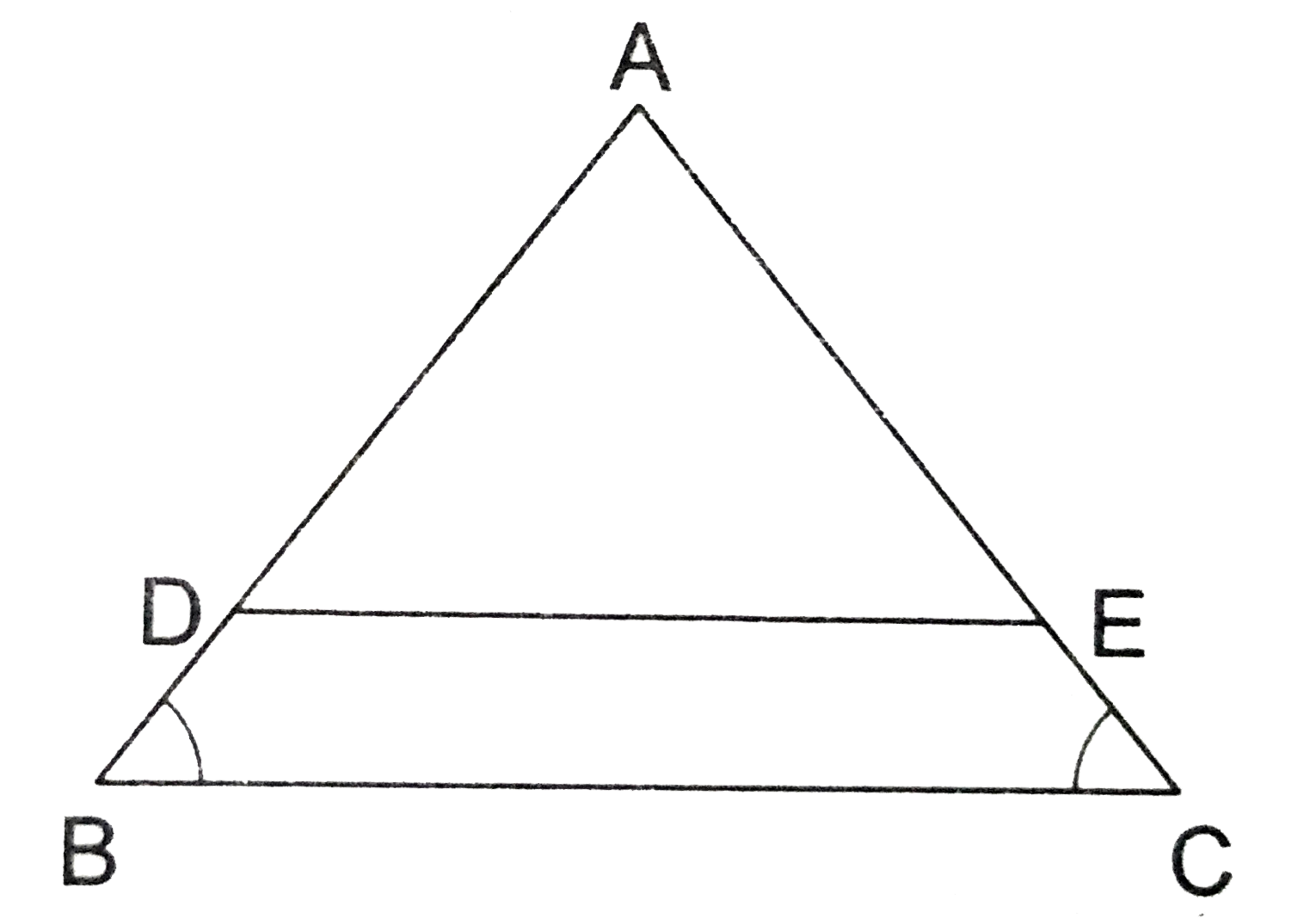
View SolutionIn the given figure, in ΔABC,∠B=∠CandBD=CE. Prove that DE∣∣BC.
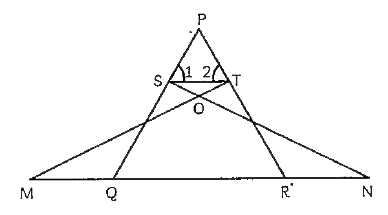
View SolutionIn the given figure, figure, if ∠1=∠2 and △NSQ≅△MTR, then prove that △PTS~△PRQ.
View SolutionIn ΔABC, ∠A+∠B=65∘,∠B+∠C=140∘ then find ∠B.
View Solution