In the given figure, ΔODC~ΔOBA,∠BOC=115∘and∠COD=70∘
Find (i) ∠DOC(ii)∠DCO(iii)∠OAB(iv)∠OBA
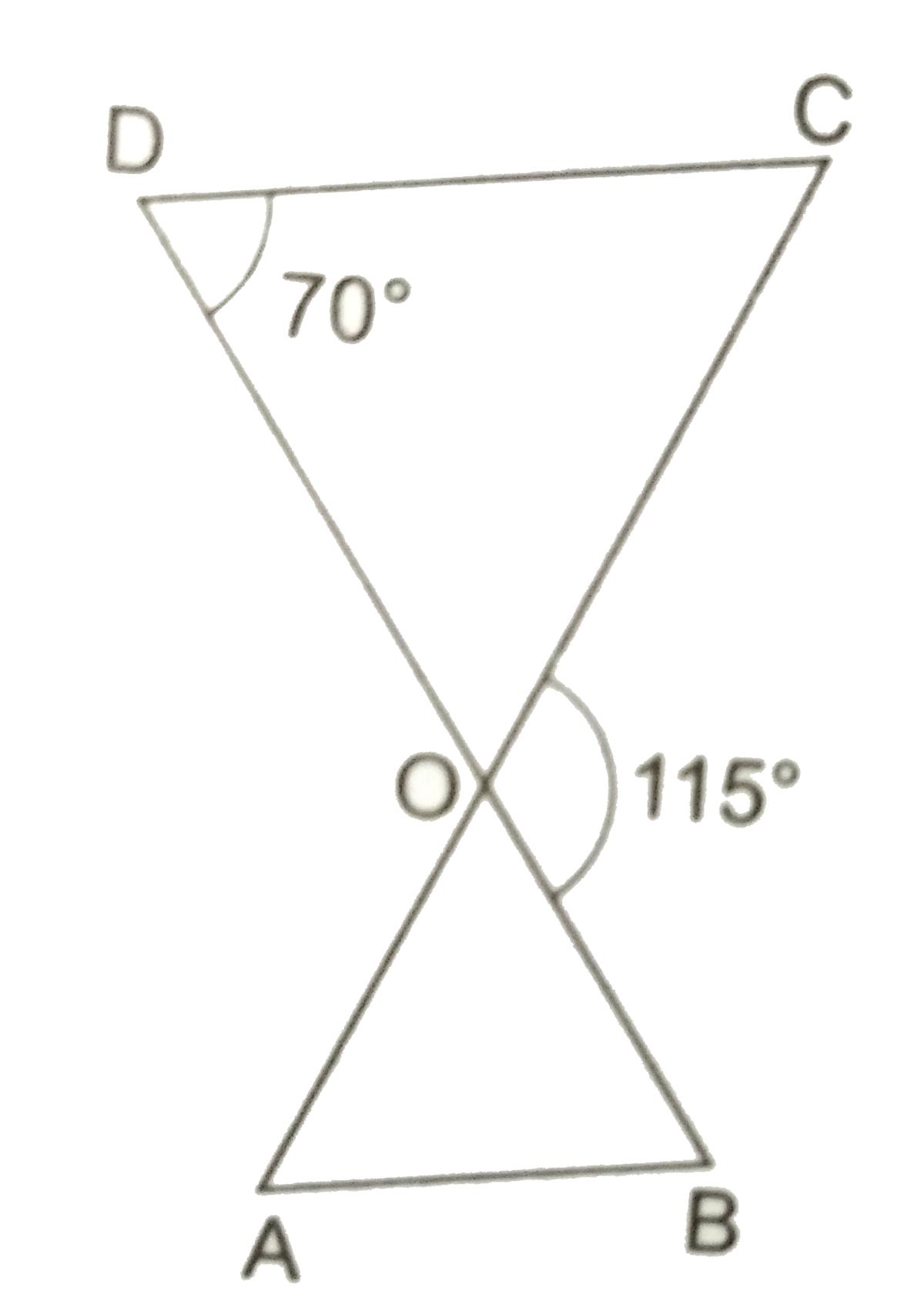
Video Solution
Text Solution
The correct Answer is:(i)∠DOC=65∘ (ii)∠DCO=45∘ (iii)∠OAB=45∘ (iv)∠OBA=70∘
∠DOC=(180∘−115∘)=65∘,∠DCO=180∘−(70∘+65∘)=45∘
ΔODC~ΔOBA⇒∠OAB=∠DCO=45∘,∠OBA=∠ODC=70∘
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7C13videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7D22videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7A12videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 1127videos
T-RATIOS OF SOME PARTICULAR ANGLES
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself20videos
TRIGONOMETRIC IDENTITIES
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure ΔODC~ΔOAB,∠BOC=125∘,∠ODC=70∘, then ∠OAB is equal to :
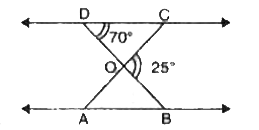 A70∘B35∘C50∘D55∘
A70∘B35∘C50∘D55∘ - Question 2 - Select One
In a ΔABC,∠A+∠B=118∘
∠A+∠C=96∘ . Find the value of ∠AA36∘B40∘C30∘D34∘
In a ΔABC∠A+∠B=145∘,2∠B+∠C=180∘ Find ∠Aand∠B
View SolutionI is the incentre of ΔABC,∠ABC=60∘ and ∠ACB=50∘. Then find ∠BIC.
View SolutionIn the given figure, chords AB and CD are equal. If ∠OBA=55∘ then ∠COD is :
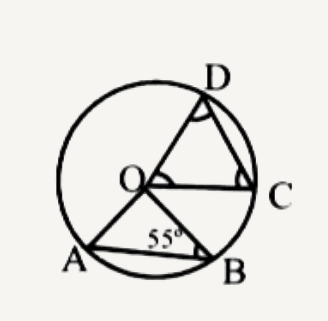 View Solution
View SolutionIn the given figure, If ∠AOB=125∘ then find ∠COD.
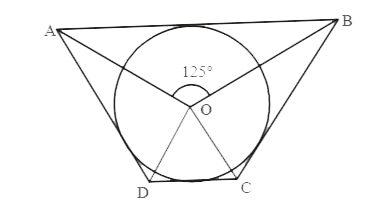 View Solution
View SolutionIn a ΔABC,∠B=100∘,∠C=70∘,AE⊥BC&AD is angle bisector . Find ∠EAD .
View SolutionIn a ΔABC,∠B=100∘,∠C=70∘,AE⊥BC&AD is angle bisector . Find ∠EAD .
View Solution