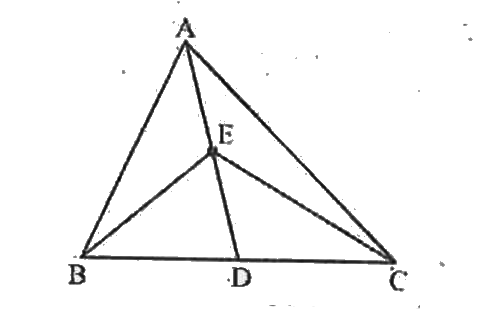
In the Given figure, E is any point on median AD of a △ABC Show that ar (ABE) = ar (ACE) Solution in Kannada
The correct Answer is:△ACE
Step by step video, text & image solution for In the Given figure, E is any point on median AD of a triangle ABC Show that ar (ABE) = ar (ACE) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Exercise 11.4
8 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE 11.2
6 Videos
- CIRCLES BOOK - CPC CAMBRIDGE PUBLICATIONCHAPTER - CIRCLES EXERCISE - EXERCISE 12.6
4 Videos
Similar Questions
Parallelogram ABCD and rectangle ABEF are on the base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
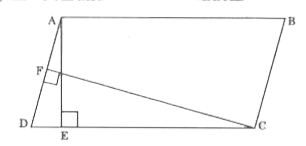
View SolutionIn the given figure, ABCD is a parallelogram , AE⊥DCandCF⊥AD . If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.
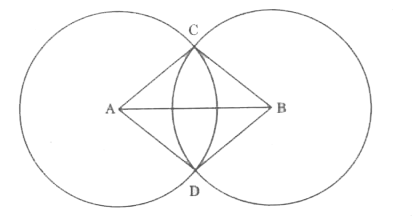
View SolutionProve that the line of centres of two intersecting circles subtends equal angles at the two point of intersection.
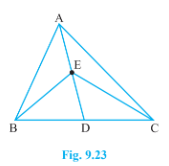
View SolutionIn Fig.9.23, E is any point on median AD of a ΔABC. Show that ar (ABE) = ar (ACE).
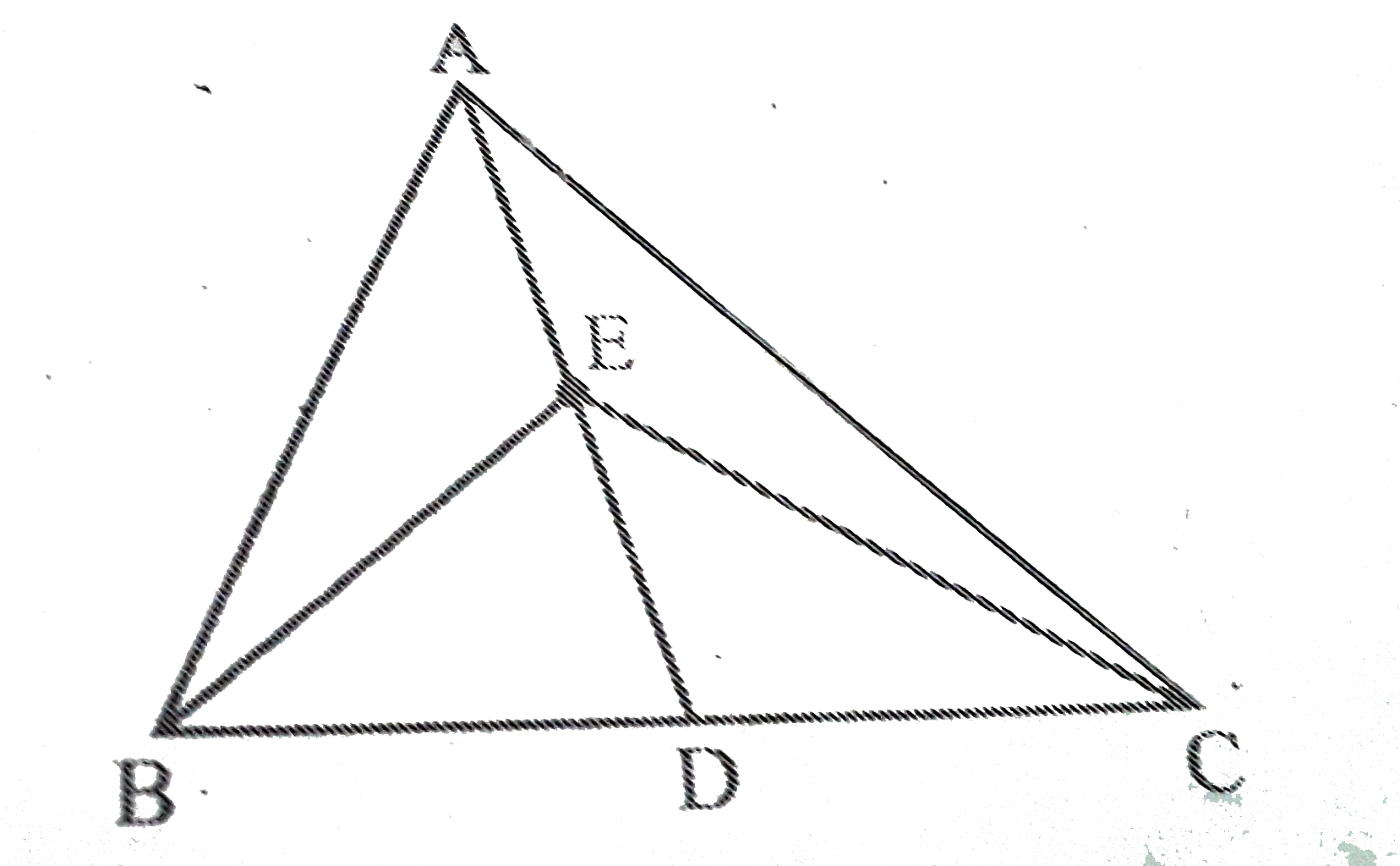
View SolutionIn the adjoining figure,E is a point on the median AD of a Delta ABC. Show that ar (Delta ABE)=(Delta ACE)
View SolutionIn an equilateral ΔABC,D is the midpoint of AB and E is the midpoint of AC. Then, ar(ΔABC):ar(ΔADE)=?

View Solutionआकृति में, ΔABC की एक मध्यिका AD पर स्थित E कोई बिंदु है दर्शाइए कि ar(ABE)=ar(ACE) है।
View SolutionΔABC की मध्यिका AD पर E कोई बिंदु है तो दिखाएँ की
ar(ΔABE)=ar(ΔACE)
View SolutionIn the figure 11.23, E is any point on median AD of a ΔABC. Show that ar (ABE) = ar (ACE).
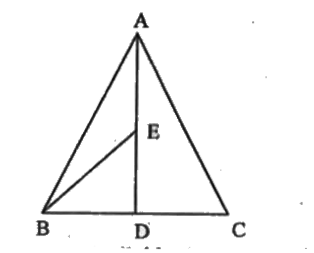
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar (BED) = 14 ar (ABC).
View SolutionIn the picture DeltaABC E is a point on the median AD. Show that - ar(ABE)=ar(ACE)
View SolutionIn the given figure ar (ΔABC)= ar (ΔADE). AC is the median of ΔADE. If ar (ACE) =14cm2 then ar (ΔABC) = ?
View SolutionIn a triangle ABC, E is the mid - point of median AD. Show that ar (BED) =1/4 ar (ABC)
View SolutionE is any point on median AD of ∠ABC .If ar(ΔABE)=10cm2 then ar(ΔACE) is
View SolutionIn a triangle ABC , E is the midpoint of median AD. Show that ar(BED) =14ar(ABC)

View Solution
