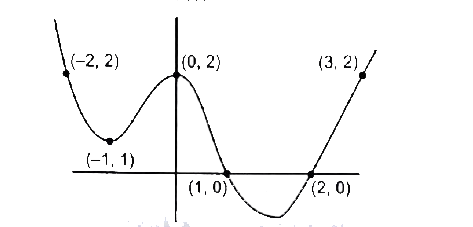
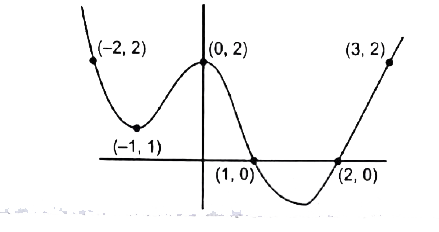
In the given figure graph of :
$y = p (x) = x^{n} + a_{1} x^{n - 1} + a_{2} x^{n - 2} + \dots . . + a_{n}$ is given.

If $p (x) + k = 0$ has 4 distinct real roots $α, β, γ, δ$ then $[α] + [β] + [γ] + [δ],$ (where [.] denotes greatest integer function) is equal to:

$- 1$

$- 2$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

Answer

Step by step video, text & image solution for In the given figure graph of : y =p (x) = x ^(n)+a_(1) x ^(n-1) +a_(2) x ^(n-2)+ …..+ a _(n) is given. If p (x) + k=0 has 4 distinct real roots alpha, beta, gamma,delta then[alpha]+[beta]+[gamma]+[delta], (where [.] denotes greatest integer function) is equal to: by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Knowledge Check

Let $f (x) = (x^{2} - 5 x + 4) (x^{2} + 5 x + 4) and α, β, γ$ (where $α < β < γ$ ) are roots of $f' (x) = 0,$ then the value of $\frac{{[α]}^{2} + [β + 1]}{[γ]}$ is equal to (where [.] denote greatest integer function)
A0
B $\frac{5}{3}$
C $\frac{5}{2}$
D5
If f(x)= $a x^{2} + b x + c, a, b, c \in$ R and eqation f(x)-x=0 has imaginary roots $α, β, γ and δ$ be the roots of f(x) -x=0 then $∣ ∣ ∣ ∣ ∣ \begin{matrix} 1 & α & δ β & 0 & α γ & β & 1 \end{matrix} ∣ ∣ ∣ ∣ ∣$ is
A0
Bpurely real
Cpurely imaginary
DNone of these

VK JAISWAL-APPLICATION OF DERIVATIVES -EXERCISE (COMPREHENSION TYPE PROBLEMS)

Home
Ask Doubt
Profile

In the given figure graph of : y=p(x)=xn+a1xn−1+a2xn−2+…..+an is given. If p(x)+k=0 has 4 distinct real roots α,β,γ,δ then[α]+[β]+[γ]+[δ], (where [.] denotes greatest integer function) is equal to:

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

Knowledge Check

Let f(x)=(x2−5x+4)(x2+5x+4)andα,β,γ (where α<β<γ) are roots of f'(x)=0, then the value of [α]2+[β+1][γ] is equal to (where [.] denote greatest integer function)

If f(x)=ax2+bx+c,a,b,c∈ R and eqation f(x)-x=0 has imaginary roots α,β,γand δ be the roots of f(x) -x=0 then ∣∣ ∣ ∣∣1αδβ0αγβ1∣∣ ∣ ∣∣ is

VK JAISWAL-APPLICATION OF DERIVATIVES -EXERCISE (COMPREHENSION TYPE PROBLEMS)

In the given figure graph of :
$y = p (x) = x^{n} + a_{1} x^{n - 1} + a_{2} x^{n - 2} + \dots . . + a_{n}$ is given.

If $p (x) + k = 0$ has 4 distinct real roots $α, β, γ, δ$ then $[α] + [β] + [γ] + [δ],$ (where [.] denotes greatest integer function) is equal to:

Let $f (x) = (x^{2} - 5 x + 4) (x^{2} + 5 x + 4) and α, β, γ$ (where $α < β < γ$ ) are roots of $f' (x) = 0,$ then the value of $\frac{{[α]}^{2} + [β + 1]}{[γ]}$ is equal to (where [.] denote greatest integer function)

If f(x)= $a x^{2} + b x + c, a, b, c \in$ R and eqation f(x)-x=0 has imaginary roots $α, β, γ and δ$ be the roots of f(x) -x=0 then $∣ ∣ ∣ ∣ ∣ \begin{matrix} 1 & α & δ β & 0 & α γ & β & 1 \end{matrix} ∣ ∣ ∣ ∣ ∣$ is