In the given figure, M is the centre of the circle Chords AB and CD are perpendicular to each other. If ∠<MAD=xand∠BAC=y
(i) express ∠AMD in terms of x.
(ii) express ∠ABD in terms of y .
(iii) Prove that : x=y

The correct Answer is:180∘−2x(ii)90∘−y
Step by step video & image solution for In the given figure, M is the centre of the circle Chords AB and CD are perpendicular to each other. If angle <MAD = x and angle BAC =y (i) express angle AMD in terms of x. (ii) express angle ABD in terms of y . (iii) Prove that : x=y by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17(B)10videos
CIRCLES
- BOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )28videos
CIRCLES
- BOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )28videos
CIRCLES
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (PROBABILITY)16videos
CHAPTERWISE REVISION EXERCISE
- BOOK - ICSECHAPTER - CONSTRUCTIONS (CIRCLES)EXERCISE - EXERCISE39videos
CONSTRUCTIONS (CIRCLES)
Similar Questions
In the adjoining figure, O is centre of the circle chords AC and BD are perpendicular to each other, ∠OAB=aand∠DBC=b. Show that a= b
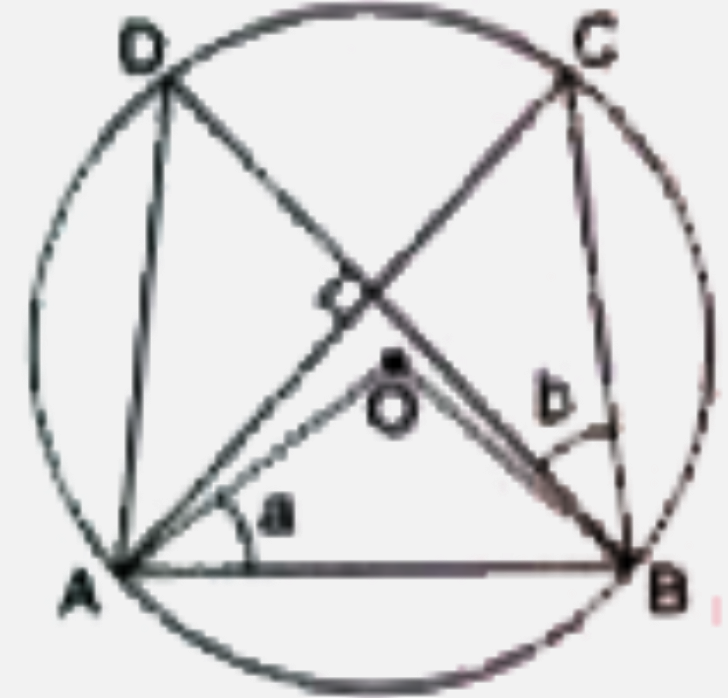 View Solution
View SolutionIn the given figure, AB∣∣CD. Find the angles x, y and z
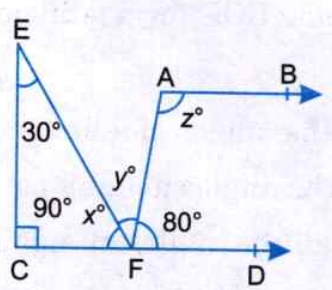 View Solution
View SolutionGiven log2x=mandlog5y=n
(i) Express 2m−3 in terms of x.
(ii) Express 53n+2 in terms of y.View SolutionIn the given figure, if x=y and AB=CB, then prove that AE=CD.
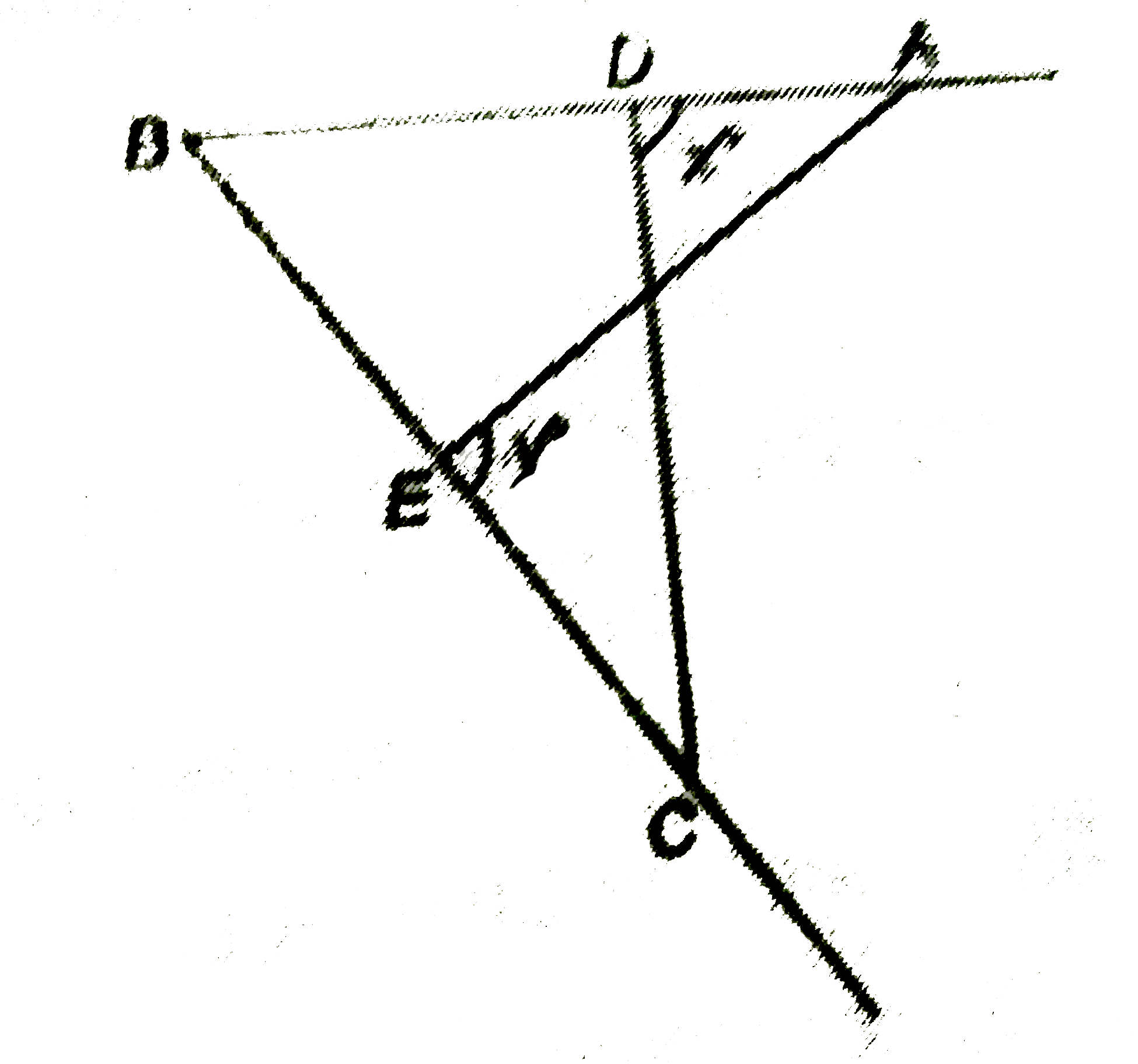 View Solution
View SolutionIn the given figure, the diameter CD of a circle with centre 0 is perpendicular to the chord AB.
If AB = 8 cm and CM = 2 cm, find the radius of the circle.
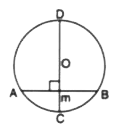 View Solution
View SolutionIn the given figure, O is the centre of a circle and ∠ADC=130∘.If ∠BAC=x∘, Find the value of x.
 View Solution
View SolutionIn the given figure BC//DE and O is the centre of the circle . If ∠CDE=x∘ , find in terms of x∘ the value of ∠BAC.
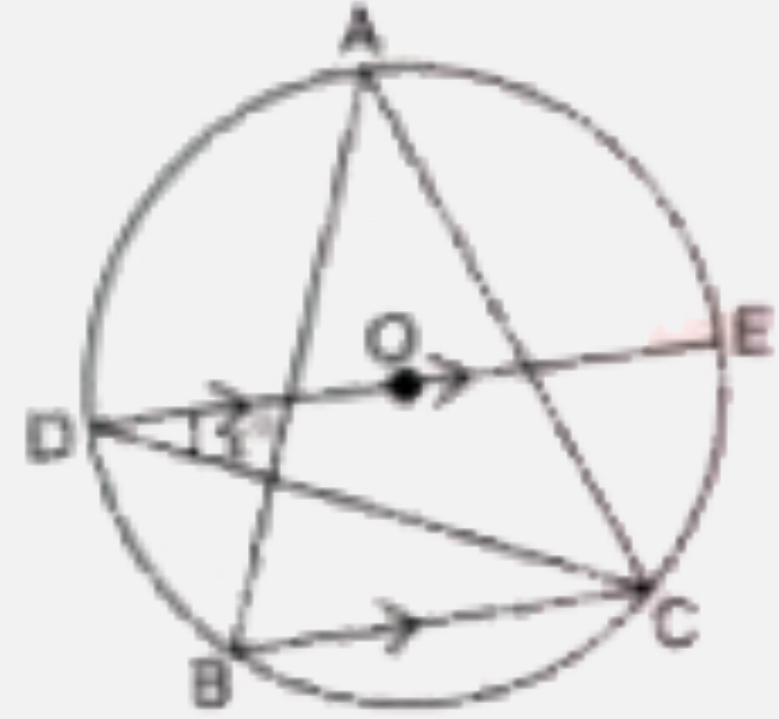 View Solution
View SolutionIn the adjoining figure, O is the centre of circle. If ∠DAB=50∘ find the values of x and y.
 View Solution
View SolutionIn circle given below . O is its centre and lengths of chords AB and CD are in the ratio 5 :3
If angle AOB = 100∘, find :
(i)∠COD
 View Solution
View SolutionIn the given 'O' is the centre of the circle, Arc AB=ArcBC=Cd.If∠OAB=48∘, find:
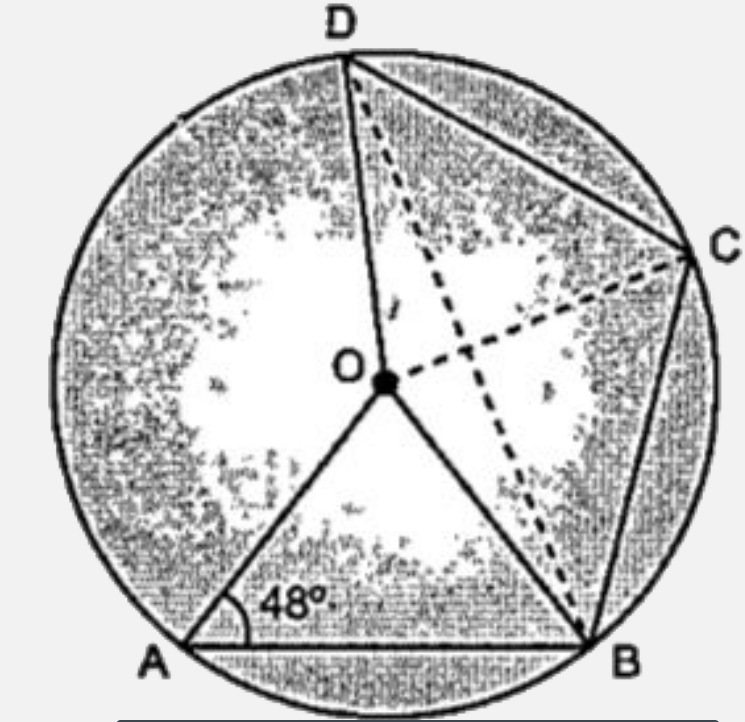
∠OBDView Solution

