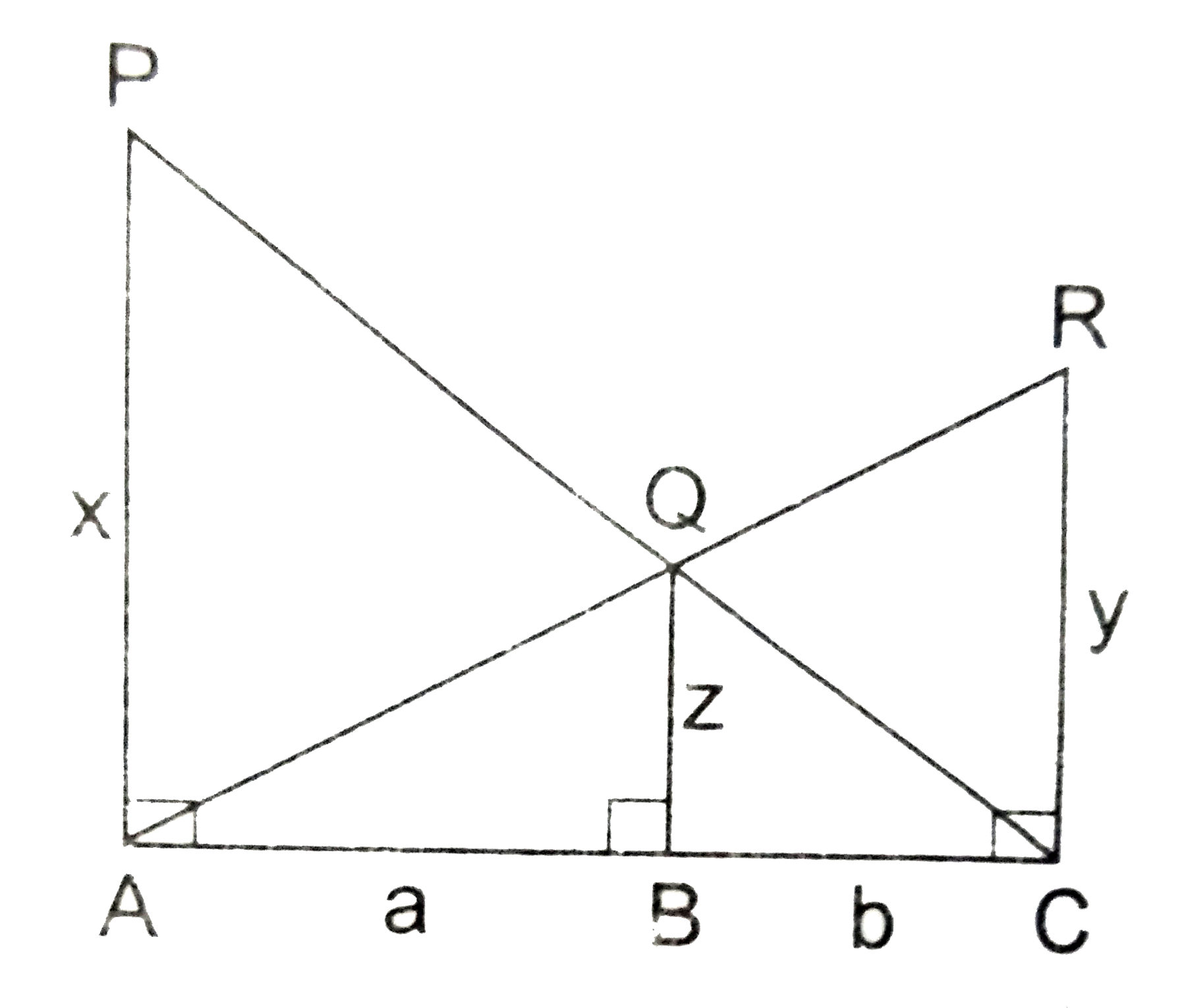
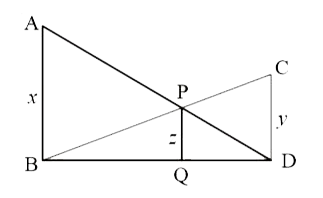
In the given figure, PA, QB and RC each is perpendicular to AC such that PA=x,RC=y,QB=z,AB=a,andBC=b
Prove that 1x+1y=1z
Video Solution
Text Solution
Pa⊥ACandQB⊥AC⇒QB∣∣PA.
Thus, in ΔPAC,QB∣∣PA, So, ΔQBC~ΔPAC.
∴QBPA=BCAC⇒zx=ba+b....(i) [ bu the propery of similar Δ ]
In ΔRAC,QB∣∣RC, So, ΔQBA~ΔRAC.
∴QBRC=ABAC⇒zy=aa+b...(ii) [ by the propert of similar Δ]
From (i) and (ii), we get
zx+zy=(ba+b+aa+b)=1
⇒zx+zy=1⇒1x+1x+1y=1z
Hence, 1x+1y=1z
|
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
Knowledge Check
In the adjoining figure PQ, QB and RC are each perpendicular to AC. Which one of the following is true :
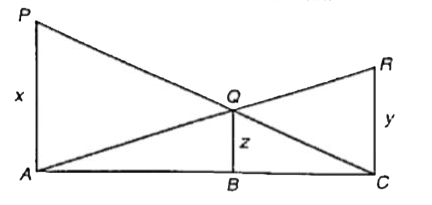 Ax+y=zBxy=2zC1x+1y=1zD1x+1y+1z=0
Ax+y=zBxy=2zC1x+1y=1zD1x+1y+1z=0
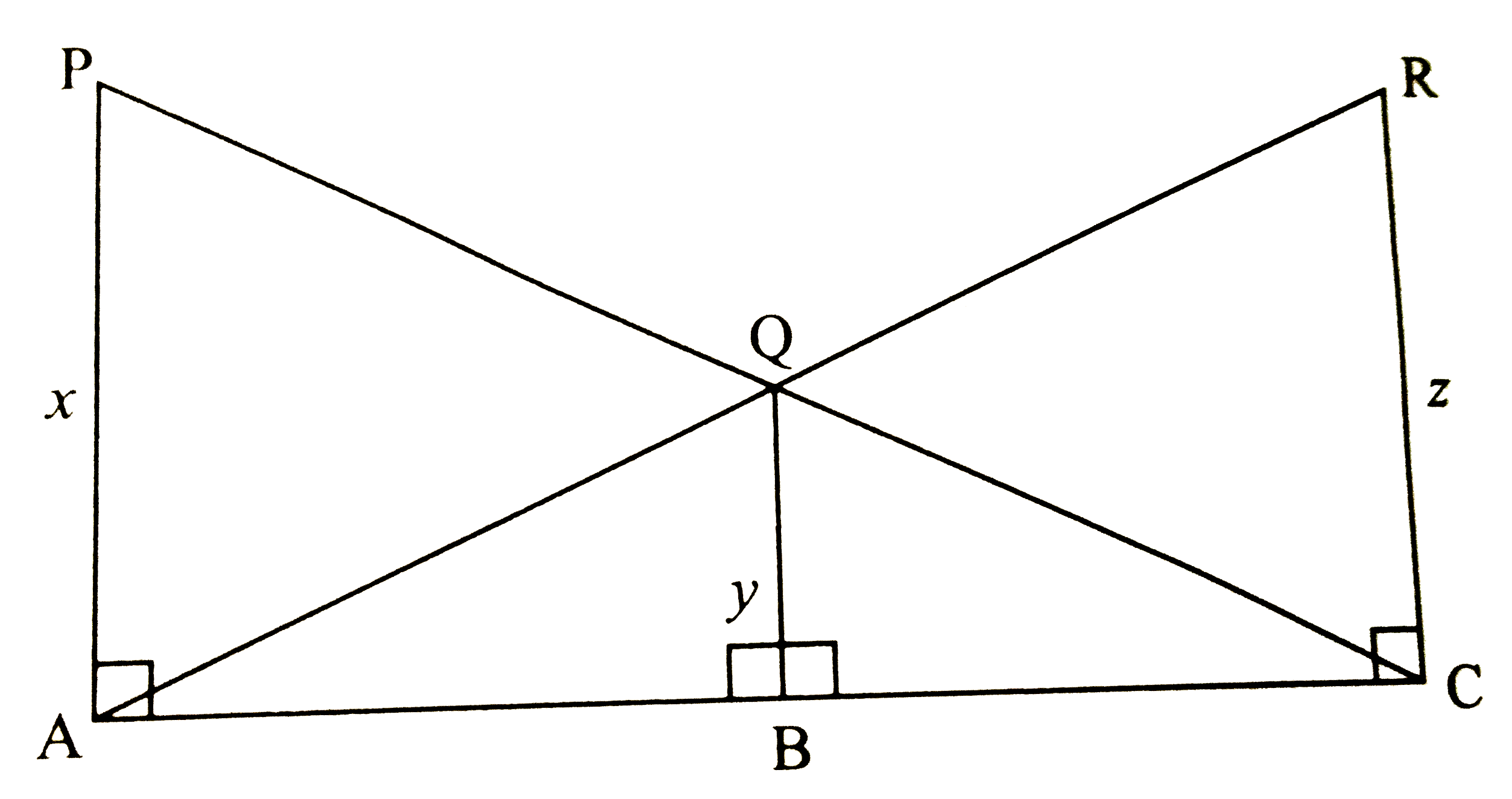
In the above figure, seg PA, seg QB and seg RC are perpendicular to seg AC. From the information given in the figure, prove that:
1x+1z=1y
View Solutionax=by=cz and b2=ac then prove that1x+1z=2y
View Solution5x=3y=15z , Prove that 1z=1x+1y
View SolutionIn the given figure AB||PQ||CD, AB = x units , CD = y units and PQ = z units, Prove that 1x+1y=1z
View Solutionif a,b,c are in G.P. and ax=by=cz prove that1x+1z=2y
View SolutionIn Fig. 4.142, PA, QB and RC are each perpendicular to AC . Prove that 1x+1z=1y . (FIGURE)
View SolutionIn the given figure AB || PQ || CD, AB=x, CD=y and PQ=z. Prove that 1x+1y=1z
View Solution