In the given figure PA=6, PB=4 and PC=8. Find PD.

The correct Answer is:3
Step by step video & image solution for In the given figure PA=6, PB=4 and PC=8. Find PD. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Chapter Assessment9videos
CIRCLE
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCLEEXERCISE - Multiple Choice Question25videos
CIRCLE
- BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - Chapter 6: Statistics4videos
CHALLENGING QUESTIONS
- BOOK - TARGET PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - CHAPTER ASSESSMENT19videos
CO-ORDINATE GEOMETRY
Similar Questions
In the given figure, if AP= PB, then
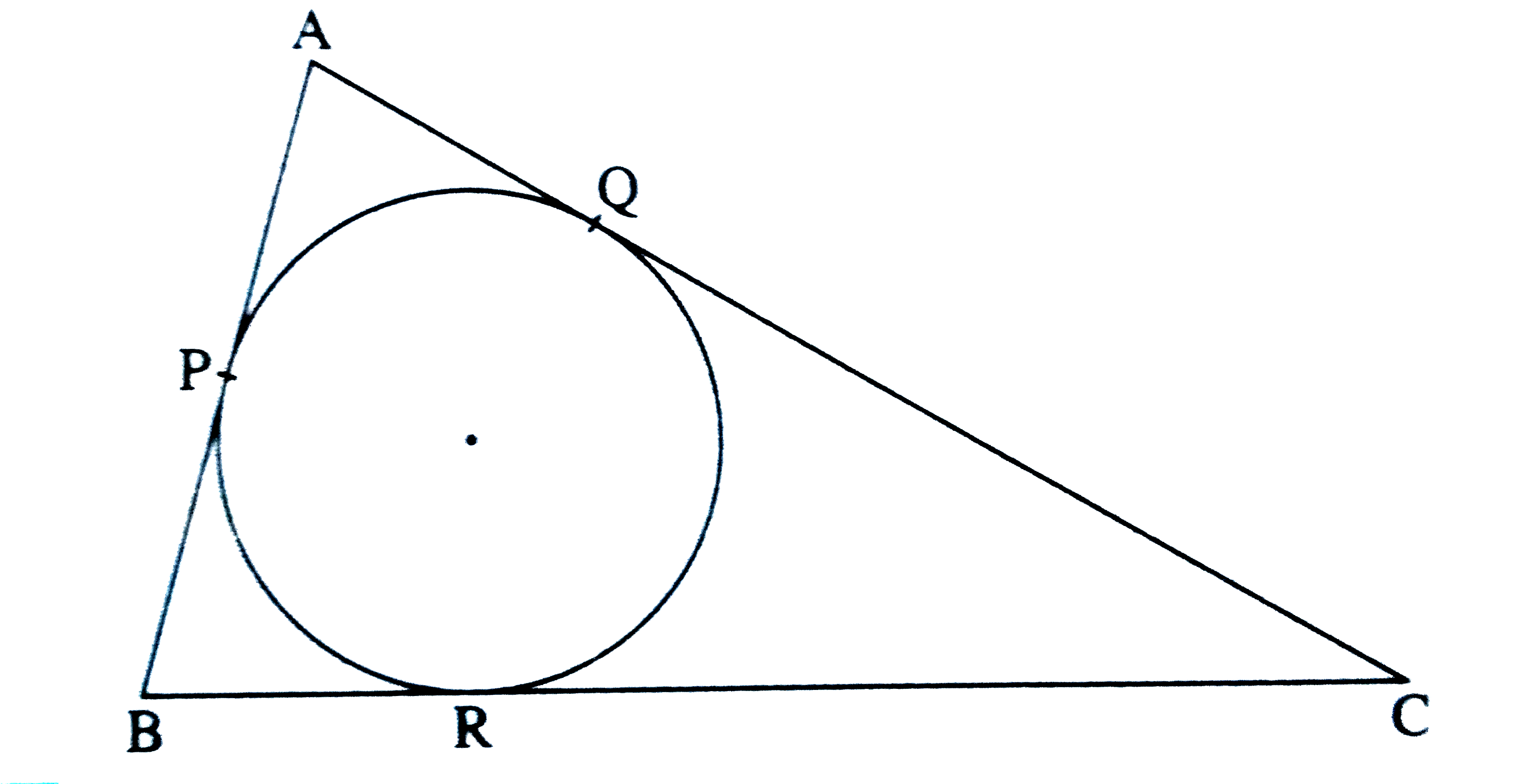 View Solution
View SolutionIn the given figure, PA, PB EC and ED are tangents to the circle, If PA=13cm,CE=4.5cm and FE=9cm. Then find PF.
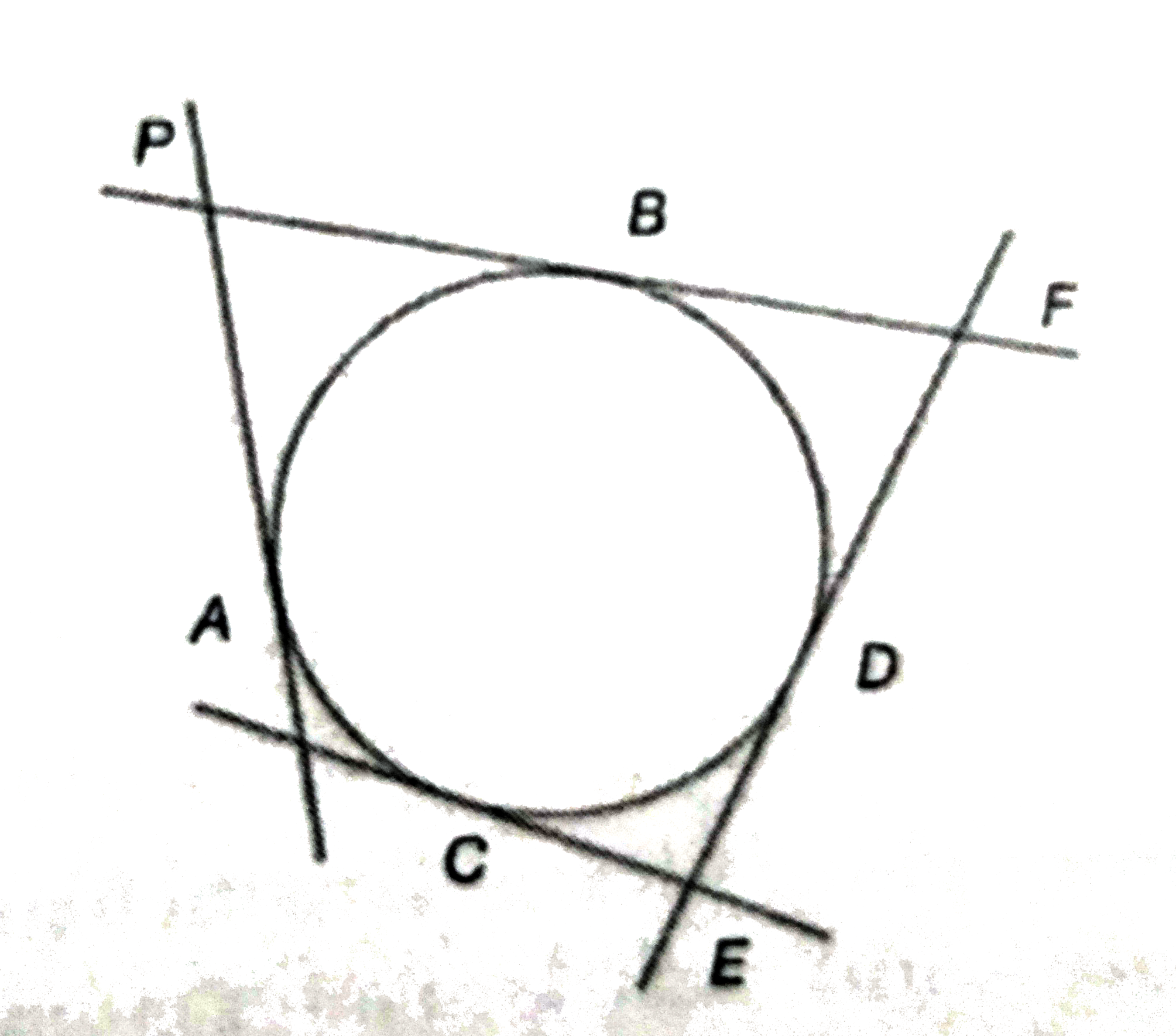 View Solution
View SolutionIn the given figure (circle), PT=5,PD=7andPA=2, then the value of PB−PC=? Fig
View SolutionIn the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA =12 cm, QC=3cm, then find PC+PD.
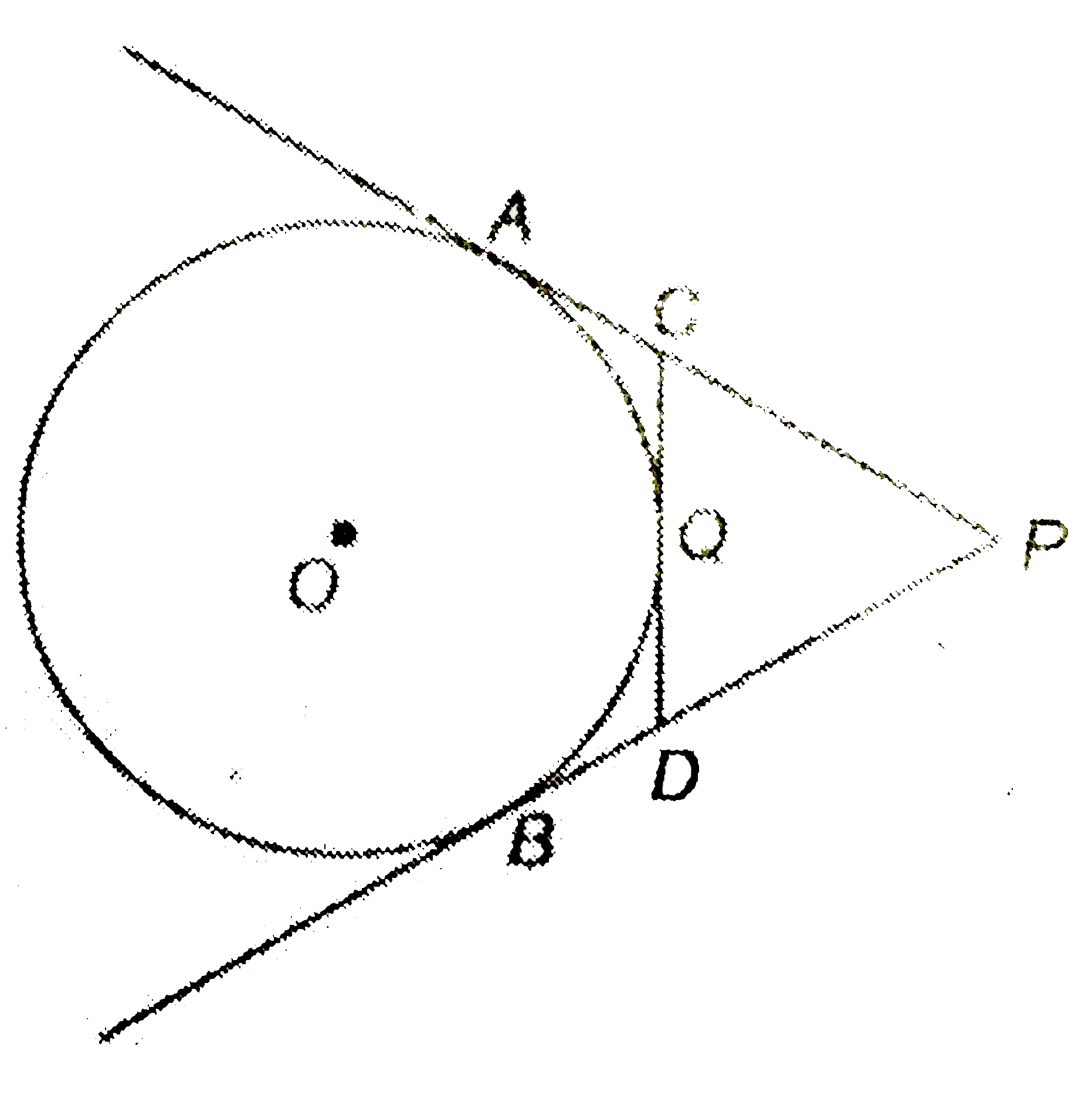 View Solution
View SolutionIn the given figure, PA, PB, EC and ED are tangents to the circle. If PA = 13 cm, CE = 4.5 cm and FE = 9 cm, then find PF.
View SolutionIn the given figure, PA and PB are tangents to a circle from an external point P such that PA=4 cm and ∠BAC=135∘. Find the length of dhord AB.
 View Solution
View SolutionIn the given figure PA and PB are tangents to the circle drawn from an external point P. CD is a third tangent touching the circle at Q. If PB=10cm and CQ=2cm. What is the length of PC?
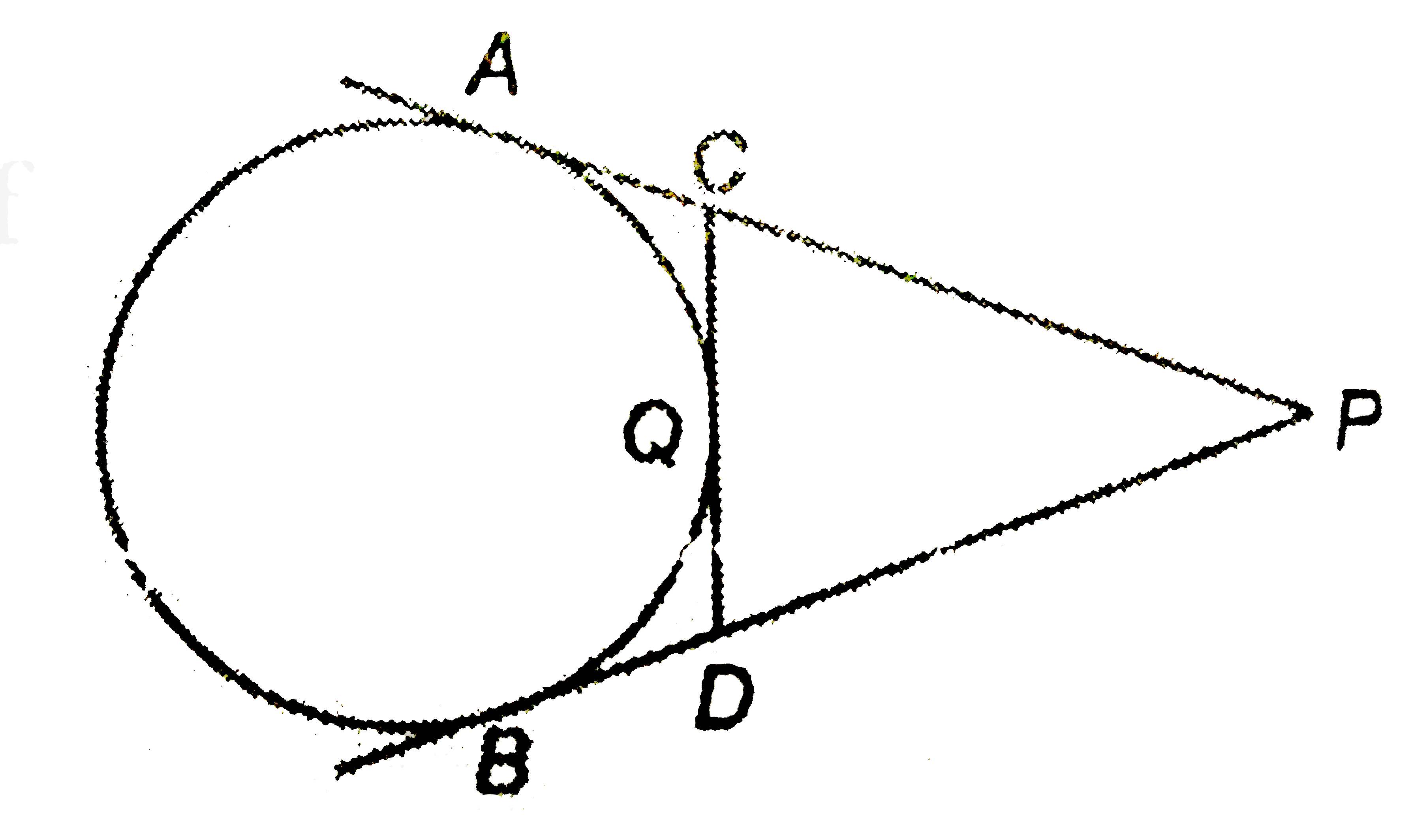 View Solution
View SolutionIn the given figure, ABCD is a square and P is a point inside it such PB = Pd. Prove that CPA is a straight line.
 View Solution
View SolutionIn the given figure PA and PB are tangents to a circle with centre O.If∠APB=(2x+3)∘ and∠AOB=(3x+7)∘ then, find the value of x.
View SolutionIn the given figure PA and PB are tangents to a circle with centre O. if ∠APB=(2x+3)∘ and ∠AOB=(3x+7)∘. then find the value of x.
View Solution

