In the given figure ,
Prove that :
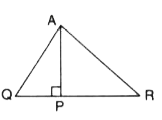
Step by step video & image solution for In the given figure , PR gt PQ Prove that : AR gt AQ by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Mid-point and intercept theorem
11 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - pythagoras therorem
9 Videos
- CHAPTERWISE REVISION (STAGE 1) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 1) EXERCISE - Triangles
18 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA
12 Videos
- CHAPTERWISE REVISION (STAGE 3) BOOK - ICSECHAPTER - CHAPTERWISE REVISION (STAGE 3) EXERCISE - DISTANCE FORMULA
11 Videos
Similar Questions
In the given figure, AP||BQ||CR. Prove that ar(ΔAQC)=ar(ΔPBR)

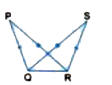
View SolutionIn the given figure, we have PQ=SR and PR=SQ. Prove that :
(i) ΔPQR≅ΔSRQ
(ii) ∠PQR=∠SRQ
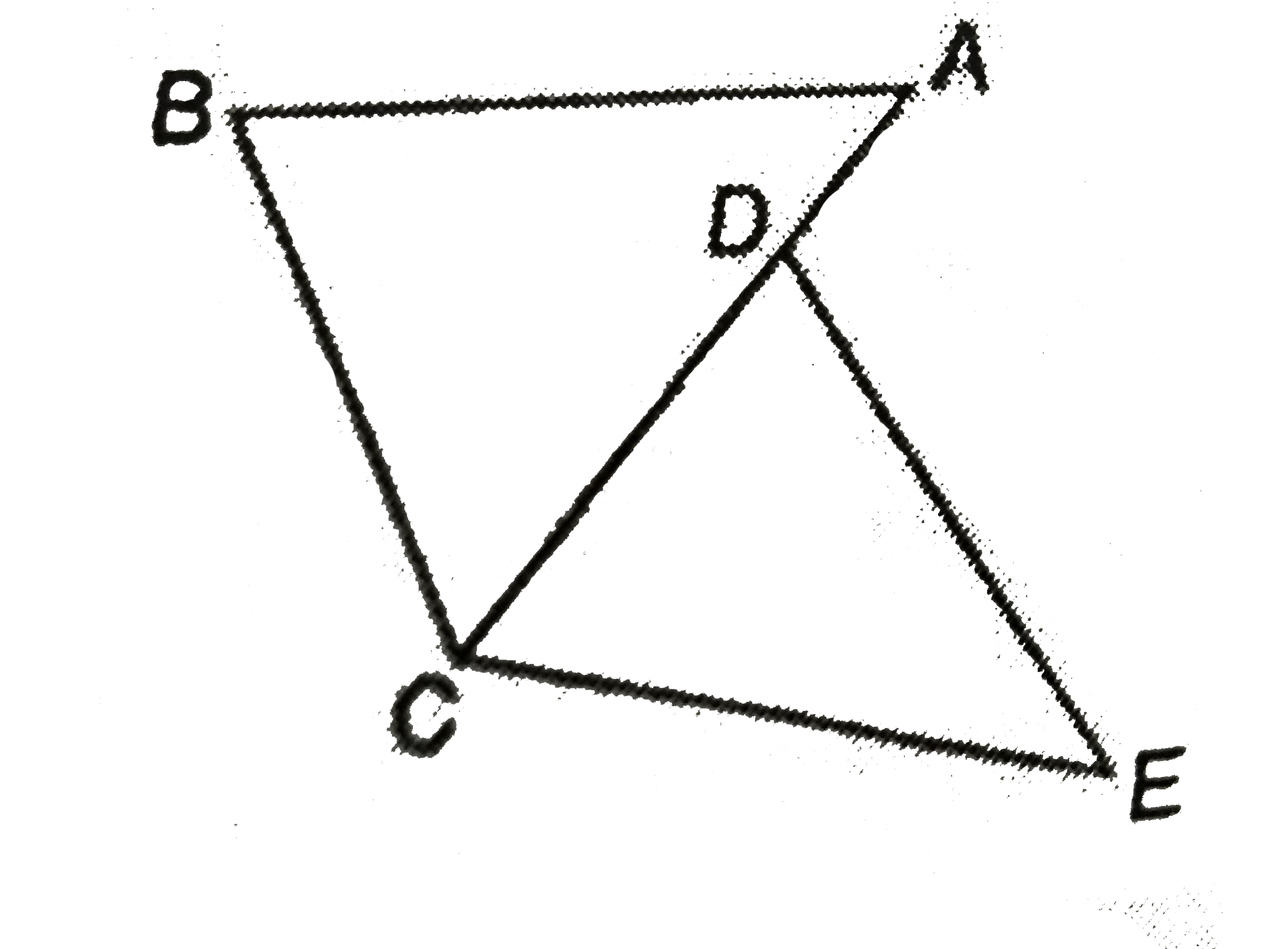
View SolutionIn the following figure, if AD=DE. Prove that :
AB+BC>CE
View SolutionIn the given figure, if DE||AQ and DF||AR. Prove that EF||QR.

View SolutionIn the given figure, P is a point on AB such that AP:PB=4:3. PQ is parallel to AC.
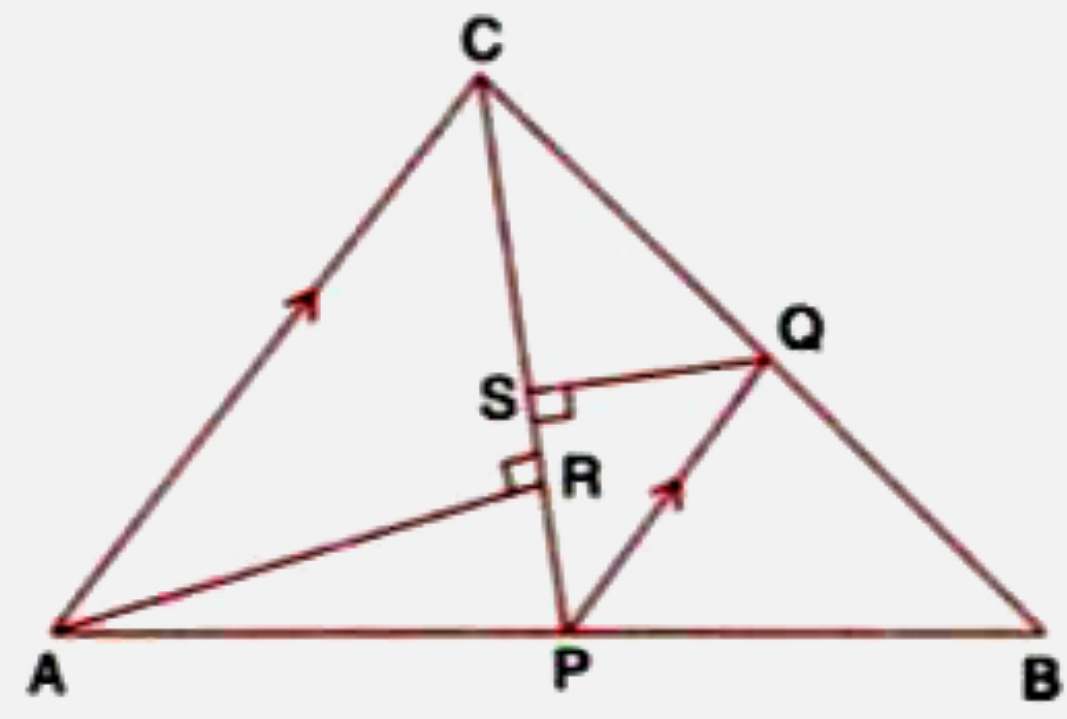
In triangle ARC,∠ARC=90∘ and in triangle PQS,,∠PSQ=90∘. Given QS=6cm, calculate the length of AR.
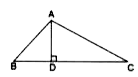
View SolutionFrom the following figure, prove that :
(i) AB>BD
(ii) AC>CD
(iii) AB+AC>BC
View SolutionIn the given figure, two tangents PQ and PR are drawn to a circle with centre O from an external point P, Prove that ∠QPR=2∠OQR.
View SolutionIn the given figure, two tangents PQ and PR are drawn to a circle with centre C from an external point P, Prove that ∠QPR=2∠OQR.
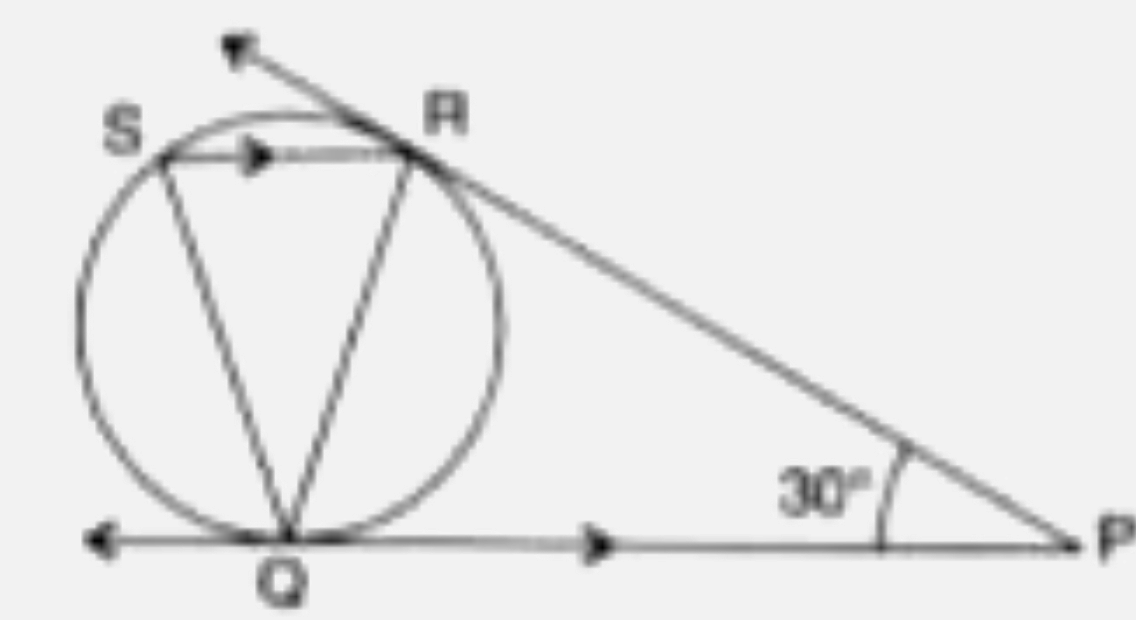
View SolutionIn the given figure, tangents PQ and PR are drawn to a circle such that angle RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the angle RQS.
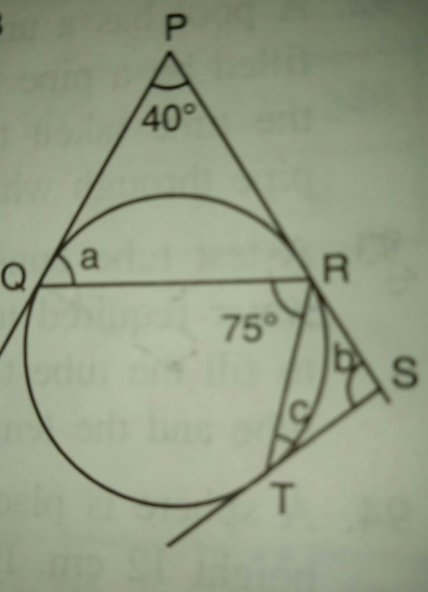
View SolutionIn the given figure, PQ, PR and ST are tangents to the same circle. If ∠P=40∘and∠QRT=75∘, find a, b and c
<
View Solution
