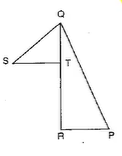
In the given figure, S and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS. Show that ΔRPQ~ΔRTS.
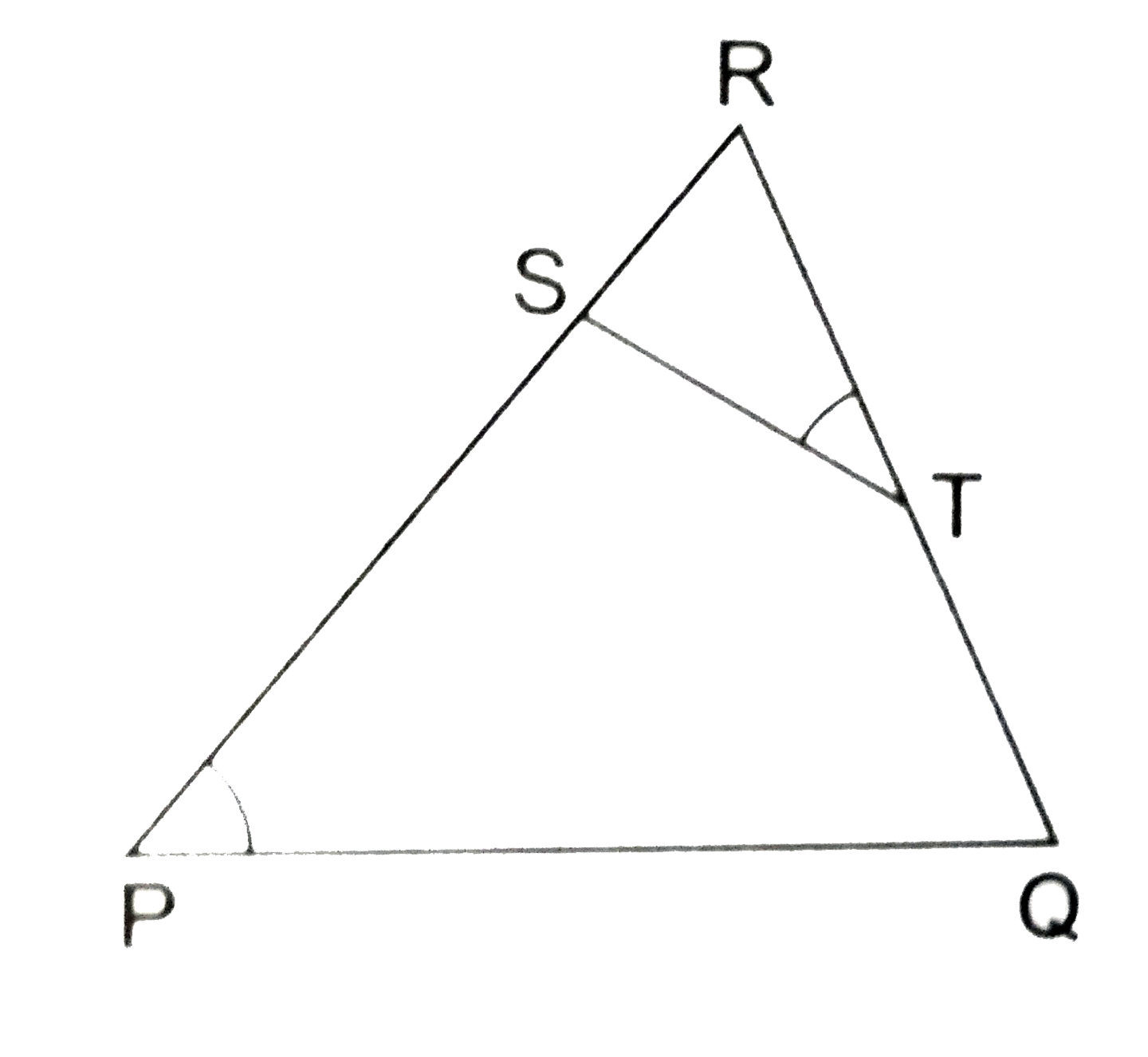
GIVEN ΔRPQandΔRTS in which ∠P=∠RTS.
TO PROVE ΔRPQ~ΔRTS.
PROOF In ΔRPQandΔRTS.
PROOF In ΔRPQandΔRTS, we have
∠P=∠RTS (given)
∠R=∠R (common)
∴ΔRPQ~ΔRTS [ by AA-similarity]
Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:SOLVED EXAMPLE
Explore 4 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:EXERCISE 7 A
Explore 1 Video
- T-RATIOS OF SOME PARTICULAR ANGLESBook:RS AGGARWALChapter:T-RATIOS OF SOME PARTICULAR ANGLESExercise:Exercise 11
Explore 27 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
Similar Questions
Knowledge Check
In the triangle PQR below, - S and T are 2 points on the sides RP and RQ respectively such that ST is parallel to PQ.
- The ratio of RT to TQ is 1:2.
The area of ΔRST = 100 sq. units.
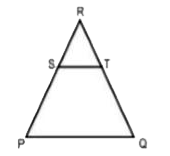
What is the area of PQTS?A200 sq. unitsB300 sq. unitsC600 sq. unitsD800 sq. units
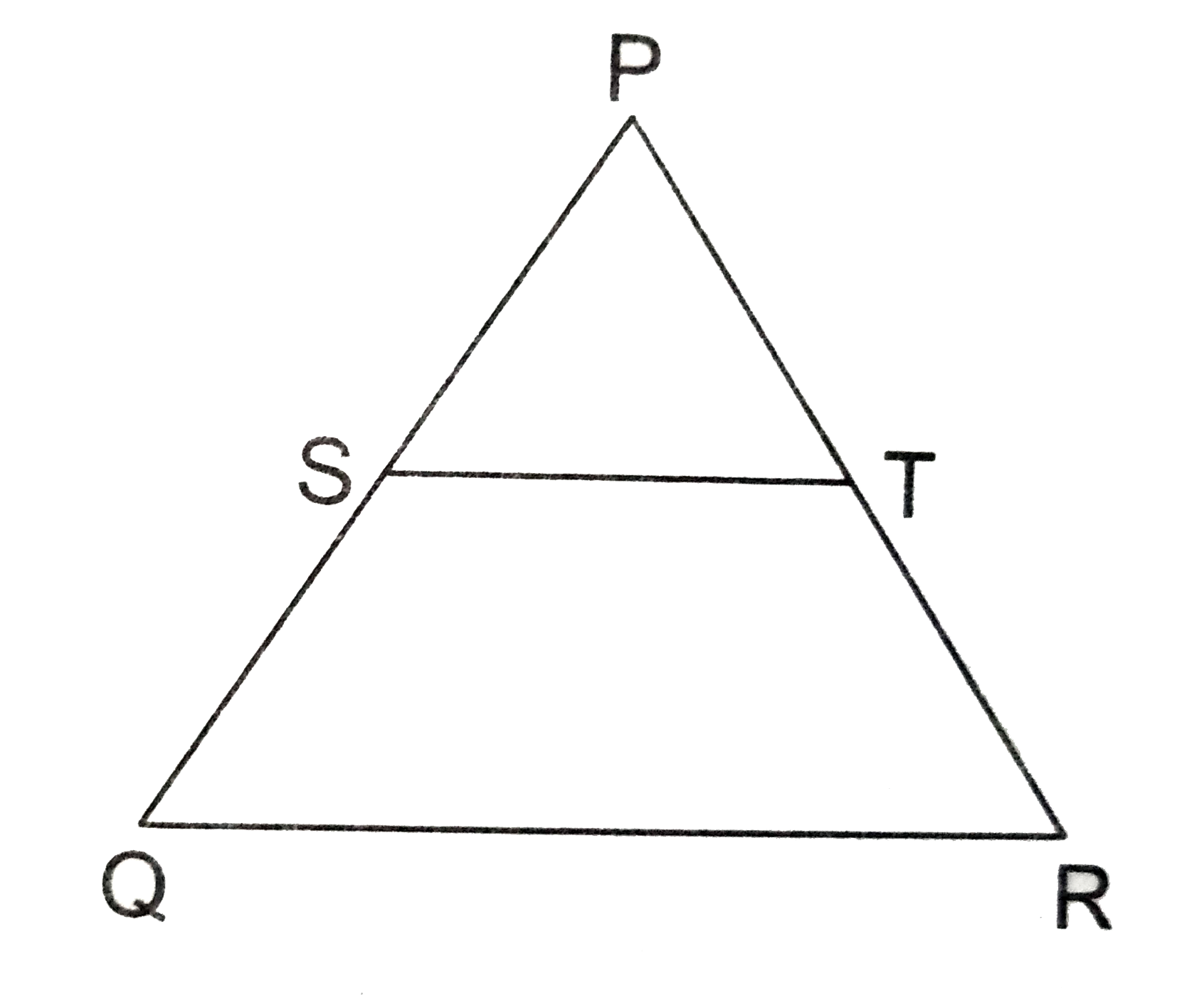
In the adjoining figure, S and T are points on the sides PQ and PR respectively of ΔPQR such that PT=2cm,TR=4cmandST is parallel to QR. Find the ratio of the ares ofΔPSTandΔPQR.
View SolutionIn ΔPQR, S is a point in QR such that angle PQS= angle SPR show that angle PSR= angle QPR
View SolutionS in any point on side QR of a ΔPQR.ShowtˆPQ + QR+RP gt 2PS.
View SolutionIn ΔPQR, point S and T are on sides Pr and PQ such that ∠PQR=∠PST. If PT= 5 cm., PS = 3 cm. And TQ = 3 cm. then length of SR will be-
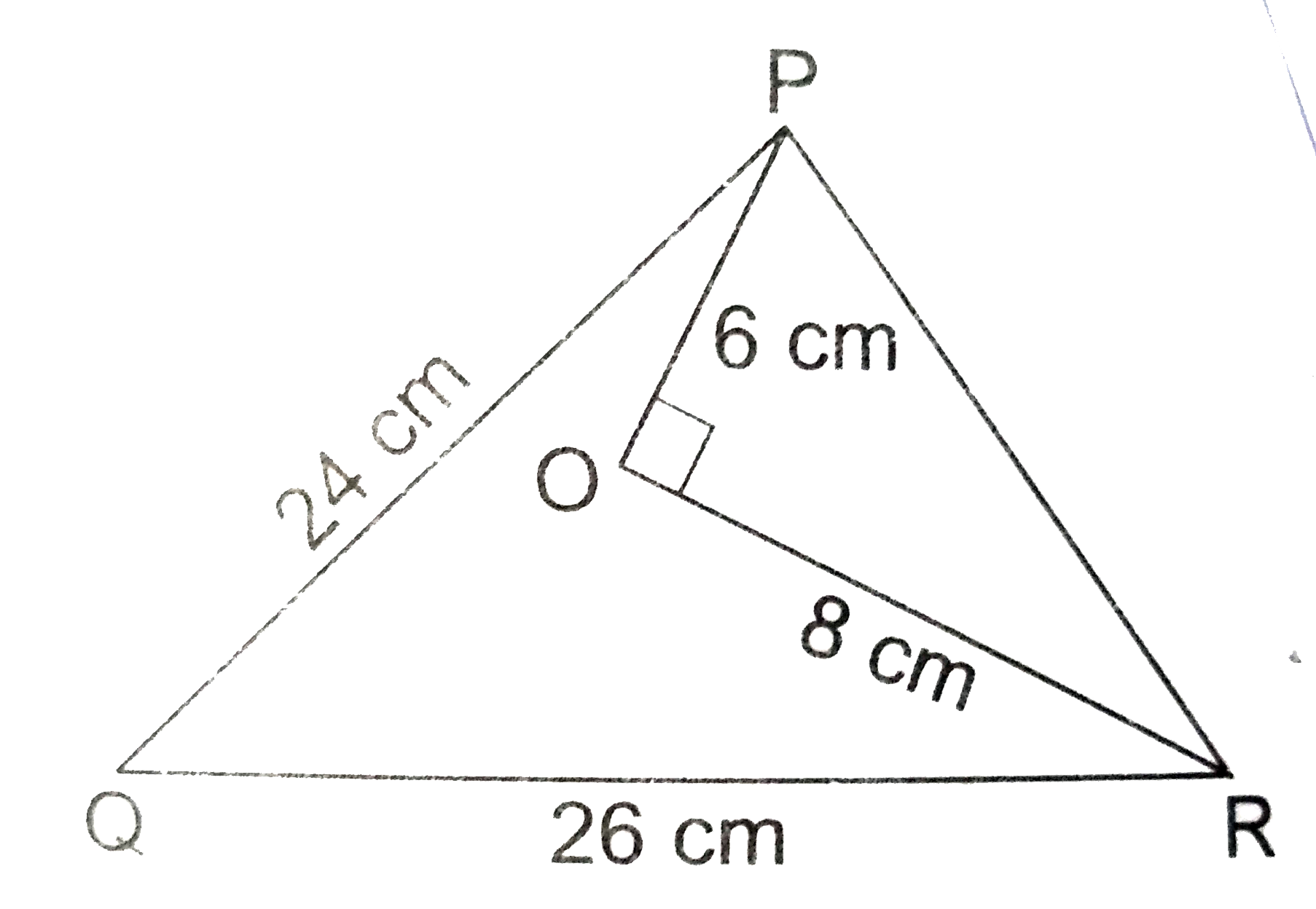
View SolutionIn the given figure, O is point inside a ΔPQR such that ∠POR=90∘,OP=6cmandOR=8cm. If PQ=24cmandQR=26cm, prove that ΔPQR is right angled.
View SolutionIn Figure, T is a point on side QR of PQR and S is a point such that RT=ST. Prove That : PQ+PR>QS
View SolutionS and T are points on the sides PQ and PR, respectively of ΔPQR, such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ΔPST and ΔPQR.
View Solution