In the given figure, the incircle of ΔABC touches the sides BC, CA and AB at P, Q and R respectively. Prove that
(AR+BP+CQ)=(AQ+BR+CP)
=12(perimeter ofΔABC).
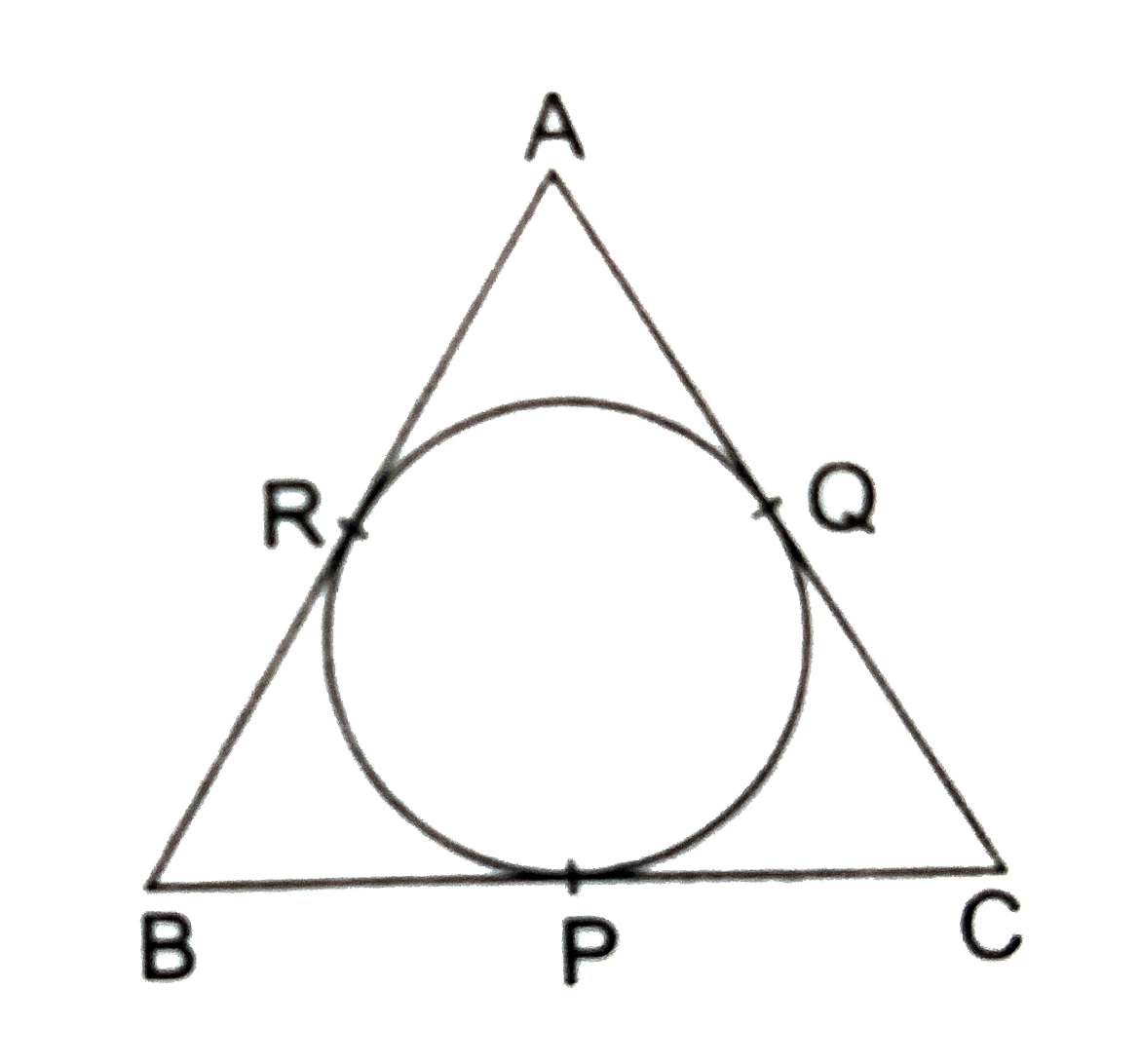
We know that the lengths of tangents from an exterior point to a circle are equal.
∴AR=AQ, ……….(i) [tangents from A]
BP=BR, ………(ii) [tangents from B]
CQ=CP ………….(iii) [tangents from C]
∴(AR+BP+CQ)=(AQ+BR+CP)=k (say).
Perimeter of ΔABC=(AB+BC+CA)
=(AR+BR)+(BP+CP)+(CQ+AQ)
=(AR+BP+CQ)+(AQ+BR+CP)
=(k+k)=2k
⇒k=12(perimeter of ΔABC) .
∴(AR+BP+CQ)=(AQ+BR+CP)
=12(perimeter ofΔABC).
Topper's Solved these Questions
- CIRCLESBook:RS AGGARWALChapter:CIRCLESExercise:Exercise 8A
Explore 16 Videos
- CIRCLESBook:RS AGGARWALChapter:CIRCLESExercise:Exercise 8B
Explore 15 Videos
- ARITHMETIC PROGRESSIONBook:RS AGGARWALChapter:ARITHMETIC PROGRESSIONExercise:Multiple Choice Questions (Mcq)
Explore 30 Videos
- CONSTRUCTIONSBook:RS AGGARWALChapter:CONSTRUCTIONSExercise:Test Yourself
Explore 10 Videos
Similar Questions
In the given figure, D, E and F are the points where the incircle of the ΔABC touches F the sides BC, CA and AB respectively. Show that AF+ BD + CE = AE + BF + CD = (perimeter of ΔABC)
View SolutionIn Fig. 10.19, the incircle of ABC touches the sides BC, CA and AB at D, E and F respectively. Show that AF+BD+CE=AE+BF+CD=12(Perimeter of ABC) (FIGURE)
View Solution
Knowledge Check
Incircle of ΔABC touches the sides BC, AC and AB at D, E and F, respectively. Then answer the following question
∠DEF is equal toAπ−B2Bπ−2BCA−CDnone of theseIncircle of ΔABC touches the sides BC, AC and AB at D, E and F, respectively. Then answer the following question
Area of ΔDEF isA2r2sin(2A)sin(2B)sin(2C)B2r2cos.A2cos.B2cos.C2C2r2sin(A−B)sin(B−C)sin(C−A)Dnone of these
The incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively . Prove that BD = DC.

View SolutionA circle touches the side BC of ΔABC at P and touches AB and AC produced at Q and R respectively. Prove that AQ=1/2(Perimeter of ΔABC).
View SolutionThe incircle of an isoceles triangle ABC, with AB=AC, touches the sides AB,BC and CA at D,E and F respecrively. Prove that E bisects BC.
View Solution25. In figure, the sides AB, BC and CA of triangle ABC touch a circle with centre and radius r at P, Q and R respectively. Prove that (i ) AB+CQ=AC+BQ (ii) Area ΔABC=12 perimeter of ΔABC).r.
View SolutionA circle is touching the side BC of ΔABC at P and touching AB and AC produced at Q and R respectively Prove that AQ=12(Perimeter of ΔABC)
View SolutionThe incircle of an isosceles triangle ABC, with AB=AC, touches the sides AB, BC, CA at D,E and F respectively. Prove that E bisects BC.
View Solution