In the given figure, there are two circles with centers A and B. The common tangent to the circles touches them, respectively,at P and Q. AR is 40cm and AB is divided by the point of contact of the circles in the ratio 5:3 What is the ratio of the length of AB to that of BR ?
1:4
2:3
2:5
7:4
The correct Answer is:2
r1r2=53=ARBR or BR=3×405=25 cm
ABBR=40−2424=1624=23
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE
6 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Matrix)
1 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- BINOMIAL THEORMBOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank
31 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
Similar Questions
In the given figure, there are two circles with centers A and B. The common tangent to the circles touches them, respectively,at P and Q. AR is 40cm and AB is divided by the point of contact of the circles in the ratio 5:3
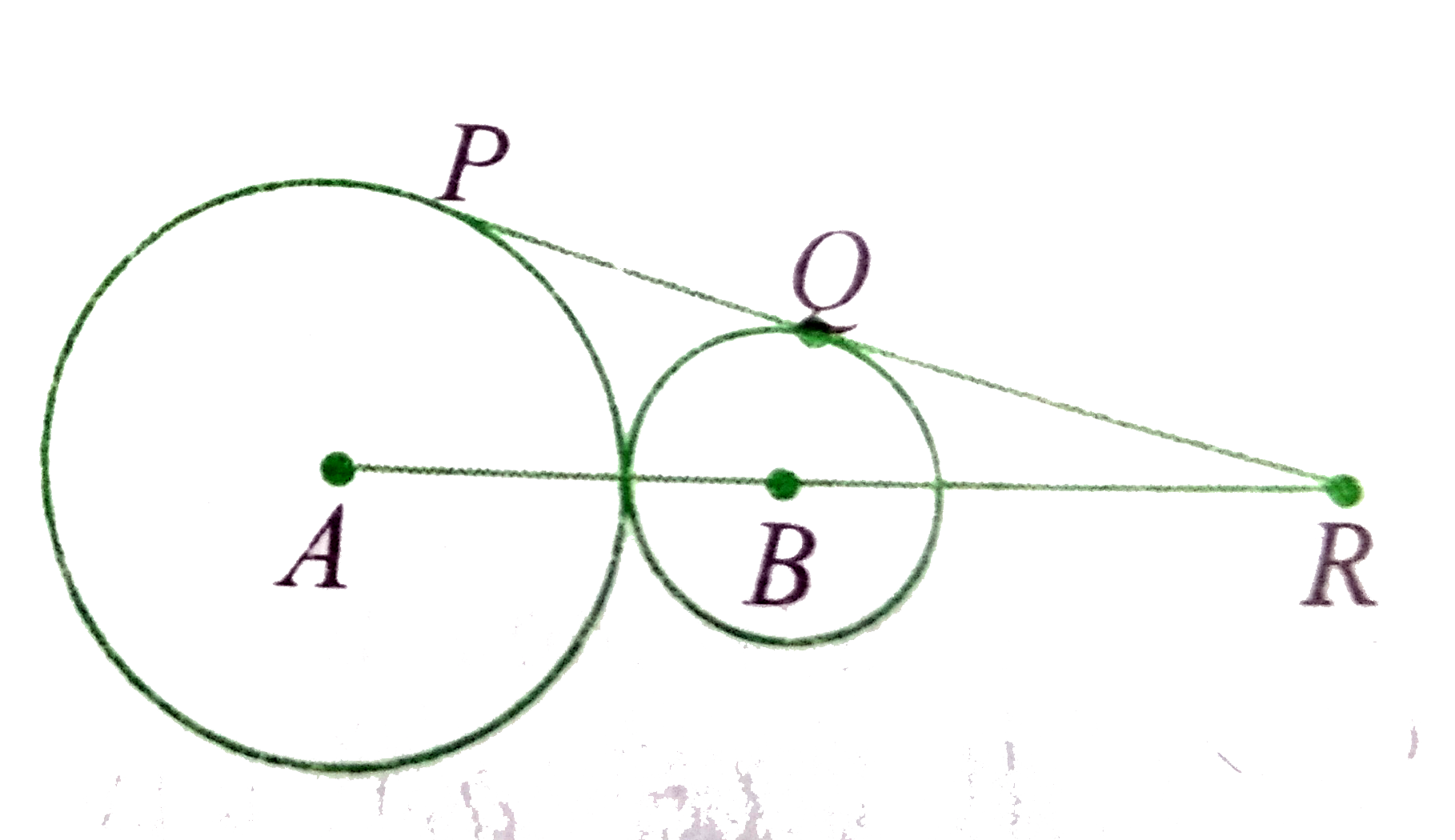
The length of QR is
View SolutionIn the given figure, there are two circles with centers A and B. The common tangent to the circles touches them, respectively,at P and Q. AR is 40cm and AB is divided by the point of contact of the circles in the ratio 5:3

The radius of the circle with center B is
View Solution
Knowledge Check
Two circles touch each other externally at point A and PQ is a direct tangent which touch circle at P and Q respectively then ∠PAQ = ?
A60∘B30∘C90∘D45∘In the given figure, B and C are the centres of the two circles. ADE is the common tangent to the two circles. If the ratio of the radius of both the circles is 3 : 5 and AC = 40, then what is the value of DE?
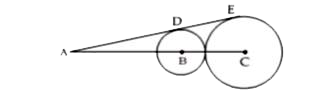 A3√15B5√15C6√15D4√15
A3√15B5√15C6√15D4√15In the given figure, AB and AC are tangents to the circle at B and C respectively and O is the centre of the circle, then x equals
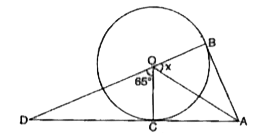 A65∘B32.5∘C57.5∘D45∘
A65∘B32.5∘C57.5∘D45∘
In the given figure two circles touch each other at the point C. Prove that the common tangent at P and Q.
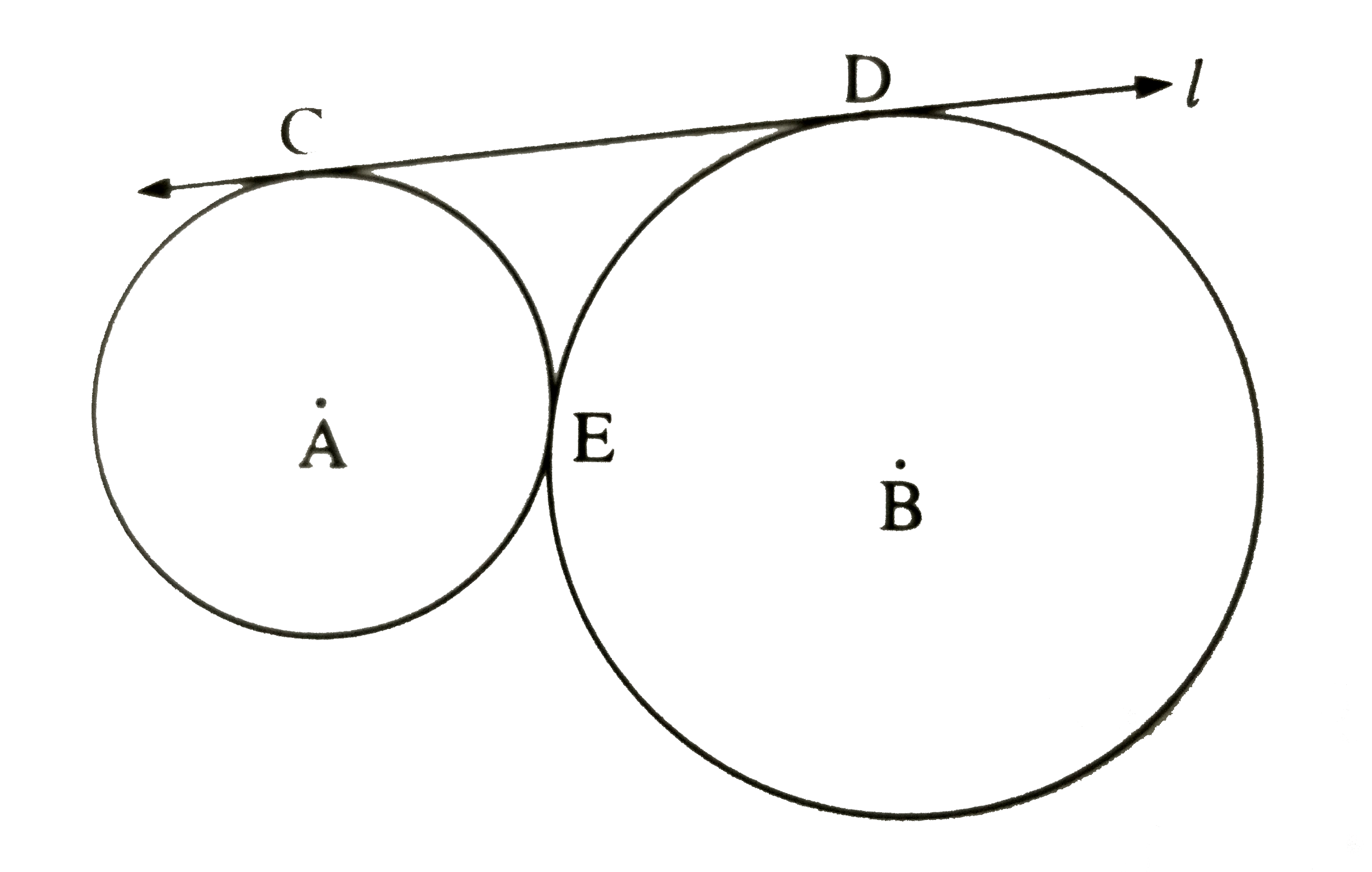
View SolutionIn the figure, the circles with centeres A and B touch each other at E. Line l is a common tangent which touches the circles at C and D respectively. Find the length of seg CD, if the radii of the circle are 4 cm, 6 cm.
View SolutionIn the given figure, centre of two circles is O. Chord AB of bigger circle intersects the smaller circle in points P and Q . Show that AP = BQ.
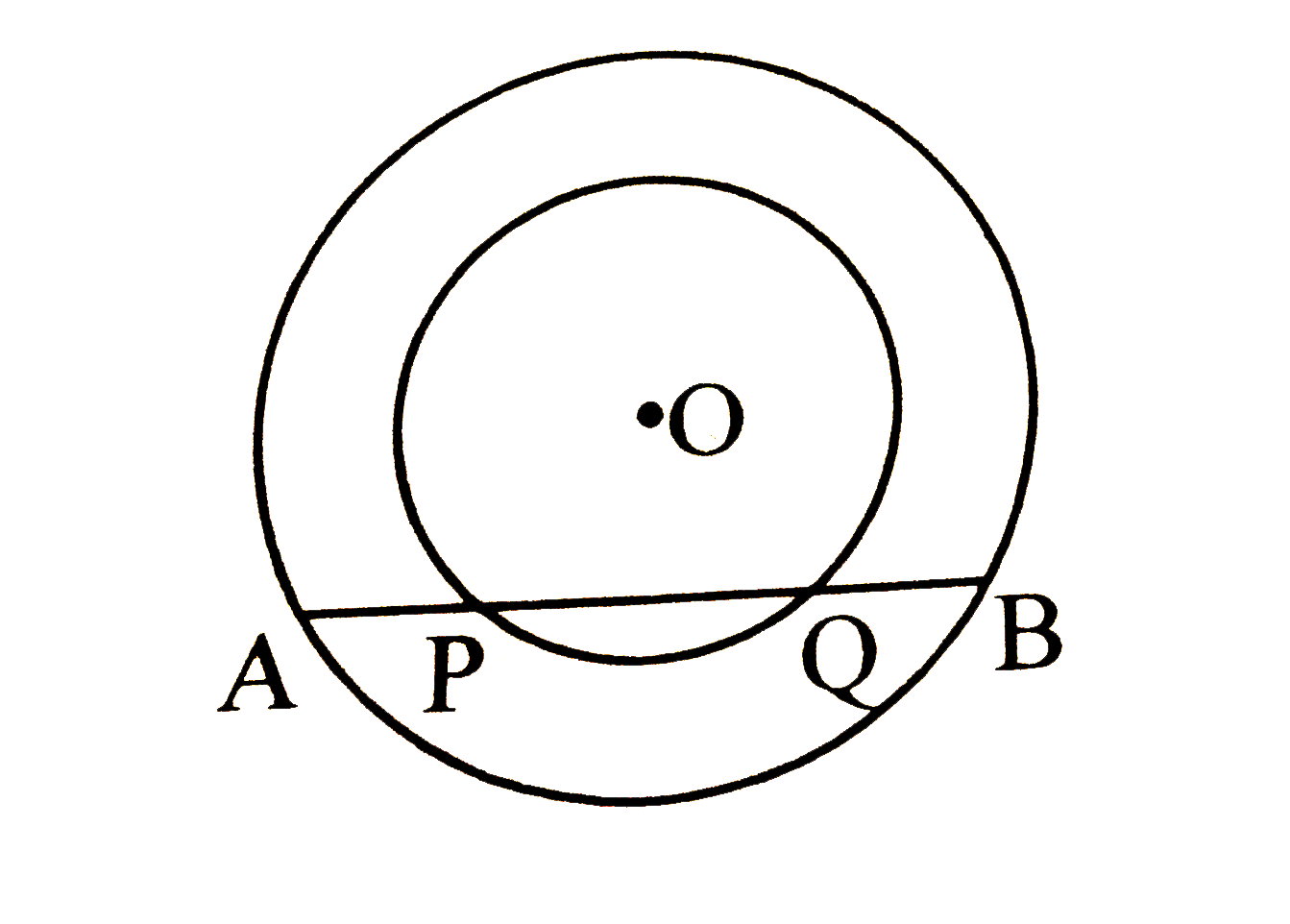
View SolutionTwo circles touch each other externally at point P. A common tangent AB is drawn touching the circles at A and B. Find ∠APB.
View SolutionIn the given figure, B and C are the centres of the two circles. ADE is the common tangent to the two circles. If the ratio of the radius of both the circles is 3 : 5 and AC = 40, then what is the value of DE?

View Solution
