In the given figure, two circles touch each other at C and AB is a tangent to both circles. Then, equal to :
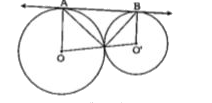
The correct Answer is:B
Topper's Solved these Questions
- CIRCLES BOOK - OSWAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
9 Videos
- CIRCLES BOOK - OSWAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - SHORT ANSWER TYPE QUESTIONS
6 Videos
- CIRCLES BOOK - OSWAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - CASE -BASED MCQs
15 Videos
- C.B.S.E 2020 CLASS -X (OUTSIDE DELHI)BOOK - OSWAL PUBLICATIONCHAPTER - C.B.S.E 2020 CLASS -X (OUTSIDE DELHI)EXERCISE - OUTSIDE DELHI SET -III ( SECTION- D )
2 Videos
- CONSTRUCTIONSBOOK - OSWAL PUBLICATIONCHAPTER - CONSTRUCTIONSEXERCISE - Assertion and Reasoning Based Questions
2 Videos
Similar Questions
Knowledge Check
The two circles touch each other if
Ac=√a2+b2B1c=1a2+1b2Cc=1a2+1b2Dc=1a2+b2
In the given figure two circles touch each other at the point C. Prove that the common tangent at P and Q.
View SolutionIn the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that:
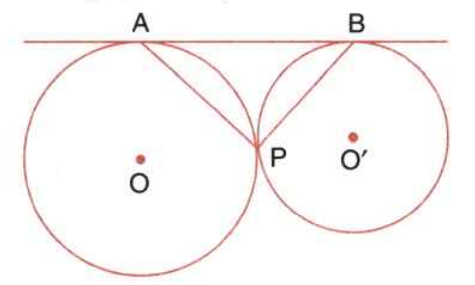
(i) tangent at point P bisects AB
(ii) angle APB=90∘
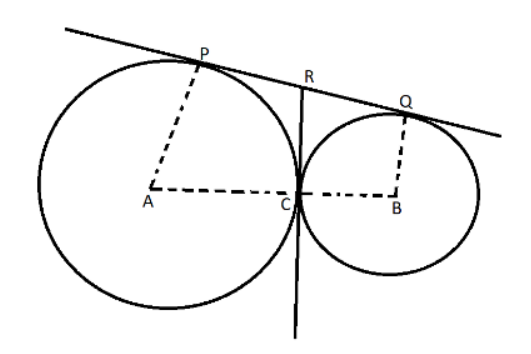
View SolutionIn the figure, two circles touch each other at the point C.Prove that the common tangents to the circles at C, bisect the common tangents at P and Q.
View SolutionIn the given figure, there are two circles with centers A and B. The common tangent to the circles touches them, respectively,at P and Q. AR is 40cm and AB is divided by the point of contact of the circles in the ratio 5:3
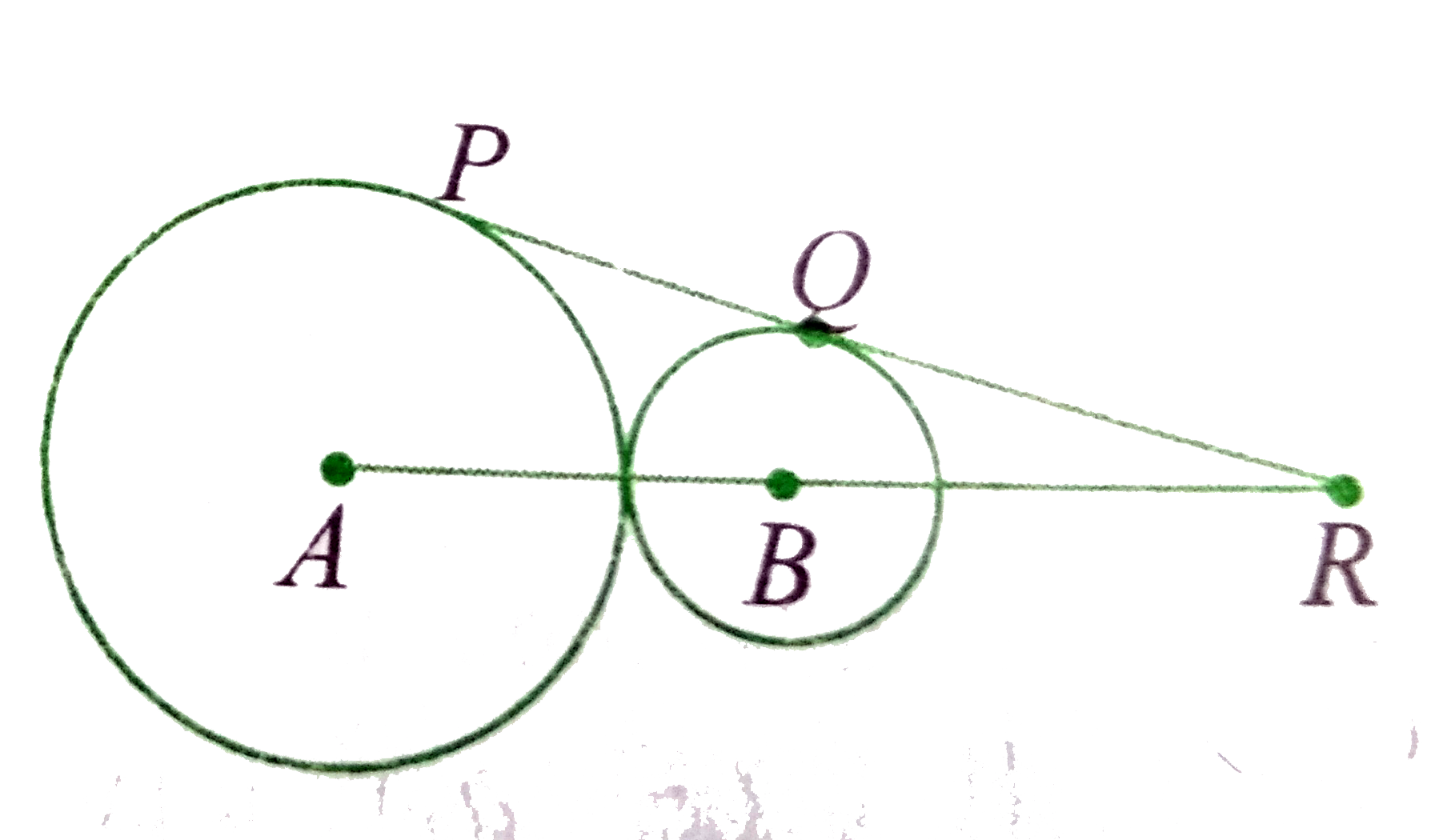
The length of QR is
View SolutionIn Figure, two circles touch each other at the point C . Prove that the common tangent to the circles at C , bisects the common tangent at P and Q .
View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.
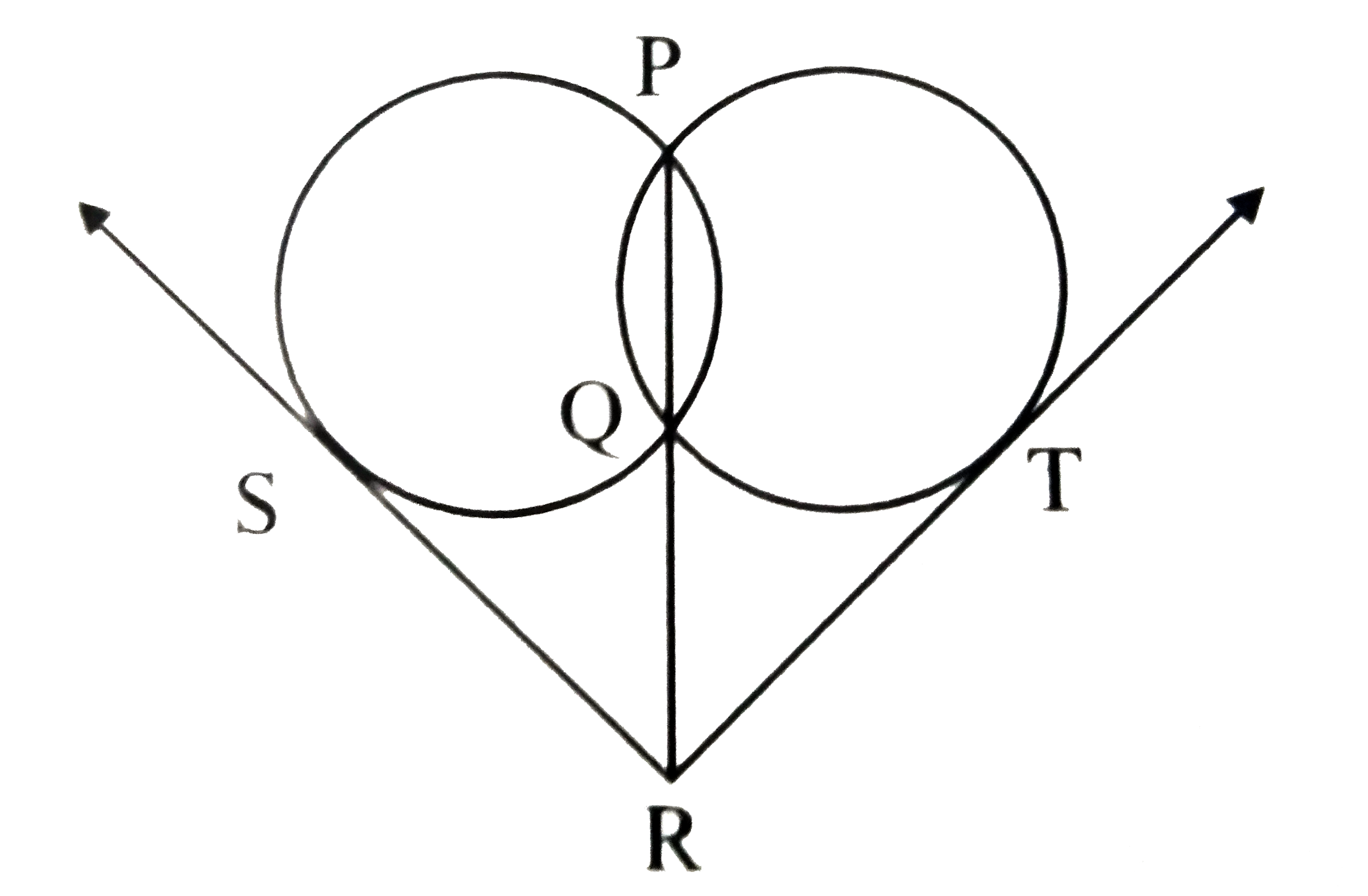
View SolutionIn the given figure two small circles touch each other externally at the centre of a big circle and these small circles are touched internally by a big circle of radius 74cm. Find the area of the shaded region

View Solution
