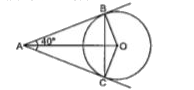
In the given figure, AB and AC are tangents to the circle with centre O such that ∠BAC=40∘. Then ∠BOC is equal to:
A
40∘
B
50∘
C
140∘
D
150∘
Text Solution
The correct Answer is:C
|
Topper's Solved these Questions
- CIRCLES BOOK - OSWAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
9 Videos
- CIRCLES BOOK - OSWAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - SHORT ANSWER TYPE QUESTIONS
6 Videos
- CIRCLES BOOK - OSWAL PUBLICATIONCHAPTER - CIRCLES EXERCISE - CASE -BASED MCQs
15 Videos
- C.B.S.E 2020 CLASS -X (OUTSIDE DELHI)BOOK - OSWAL PUBLICATIONCHAPTER - C.B.S.E 2020 CLASS -X (OUTSIDE DELHI)EXERCISE - OUTSIDE DELHI SET -III ( SECTION- D )
2 Videos
- CONSTRUCTIONSBOOK - OSWAL PUBLICATIONCHAPTER - CONSTRUCTIONSEXERCISE - Assertion and Reasoning Based Questions
2 Videos
Similar Questions
Knowledge Check
In the given figure, if PA and PB are tangents to the circle with centre O such that ∠APB=54∘, then ∠ OAB equals
A36∘B18∘C27∘D36∘AB and AC are tangents to the circle with centre O. Then x equals.
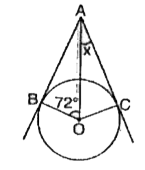 A22∘B18∘C20∘D36∘
A22∘B18∘C20∘D36∘In the given figure, AB and AC are tangents to the circle with centre O. Given that ∠BAC=70∘ and P is a point on the minor are BC, find ∠ BPC.
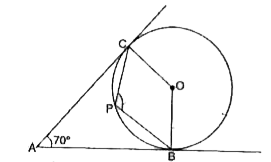 A110∘B140∘C125∘D136∘
A110∘B140∘C125∘D136∘
In the given figure , if TP and TQ are the two tangents to a circle with centre O so that ∠POQ=110∘ , then ∠PTQ is equal to
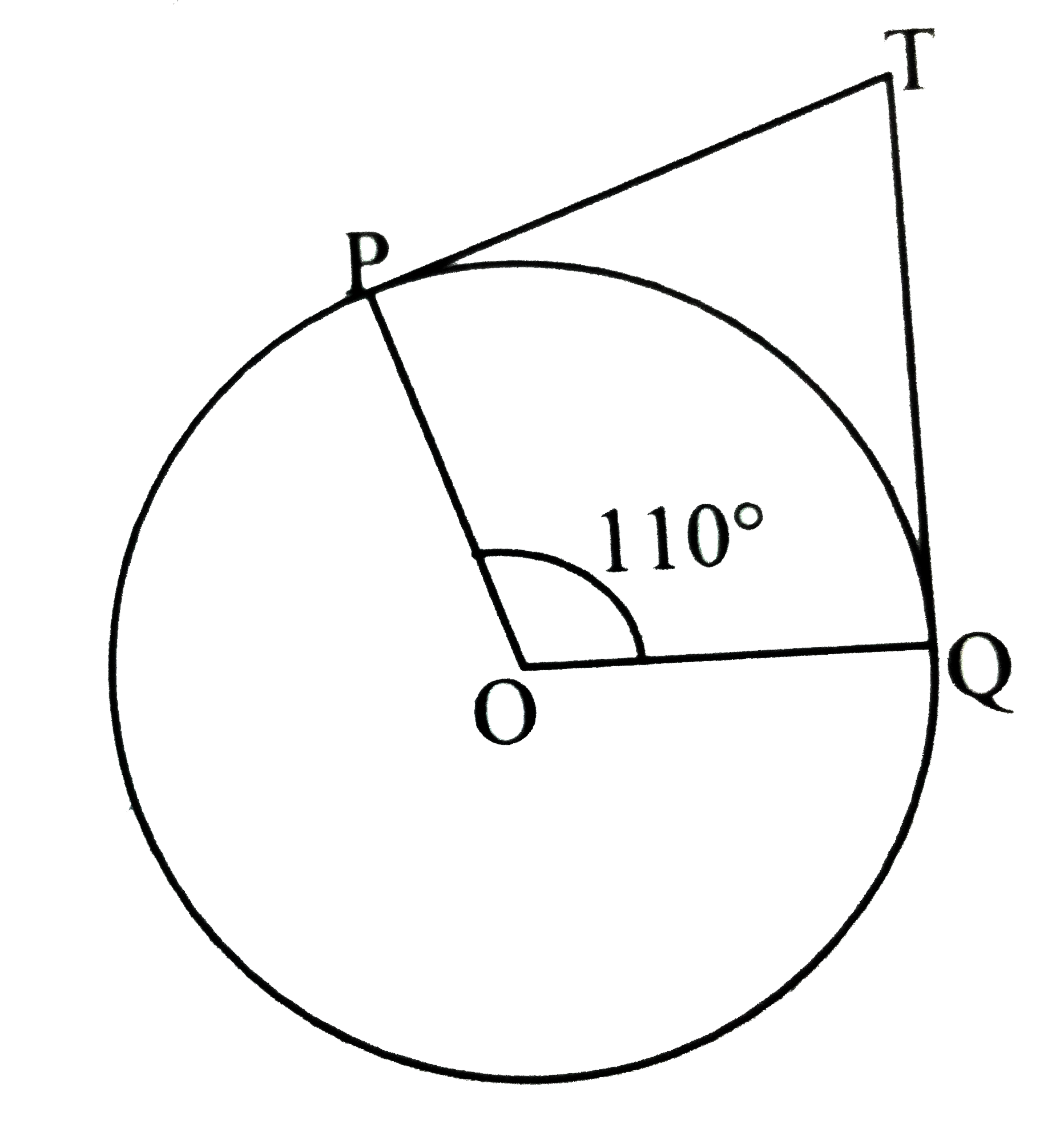
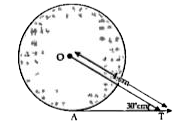
View SolutionIn the given figure ,AT is a tangent to the circle with centre O such that OT =4 cm and ∠OTA=30∘ .Then AT is equal to :
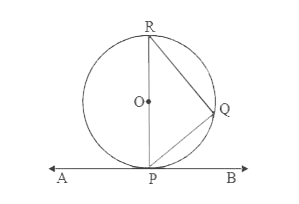
View SolutionIn the given figure, AB is a tangent to a circle with centre O. Prove ∠BPQ=∠PRQ.
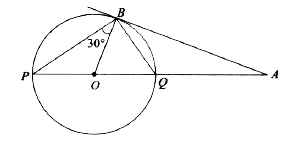
View SolutionIn the given figure , AB is a tangent to the circle with centre O and ∠BPQ=40∘ . Find PQ : AQ.
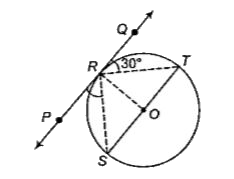
View SolutionIn the given figure, PQ is a tangent at a point R of the circle with centre O. If ∠TRQ=30∘, then ∠PRS is equal to
View Solution
