In the given figure, XY ||QR and PXXQ=PYYR=12, find XY : QR.
To solve the problem, we need to find the ratio of the lengths of line segments XY and QR given that XY is parallel to QR and the ratios of certain segments are provided.
1. Identify the Given Ratios:
We are given that PXXQ=PYYR=12.
2. Express the Segments in Terms of a Variable:
Let PX=x and XQ=2x. Therefore, the total length PQ=PX+XQ=x+2x=3x.
Similarly, let PY=y and YR=2y. Thus, the total length PR=PY+YR=y+2y=3y.
3. Set Up the Similar Triangles:
Since XY is parallel to QR, triangles PXY and PQR are similar by the Basic Proportionality Theorem (also known as Thales' theorem). This gives us the relationships:
PXPQ=PYPR=XYQR
4. Calculate the Ratios:
From our expressions:
PXPQ=x3x=13
PYPR=y3y=13
5. Establish the Ratio of XY to QR:
Since PXPQ=PYPR=XYQR, we have:
XYQR=13
6. Conclusion:
Therefore, the ratio of XY to QR is:
XY:QR=1:3
We are given that PXXQ=PYYR=12.
Let PX=x and XQ=2x. Therefore, the total length PQ=PX+XQ=x+2x=3x.
Similarly, let PY=y and YR=2y. Thus, the total length PR=PY+YR=y+2y=3y.
Since XY is parallel to QR, triangles PXY and PQR are similar by the Basic Proportionality Theorem (also known as Thales' theorem). This gives us the relationships:
PXPQ=PYPR=XYQR
From our expressions:
PXPQ=x3x=13
PYPR=y3y=13
Since PXPQ=PYPR=XYQR, we have:
XYQR=13
Therefore, the ratio of XY to QR is:
XY:QR=1:3
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - TRIANGLEEXERCISE - Short Answer Type Questions-I10videos
TRIANGLE
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - TRIANGLEEXERCISE - Short Answer Type Questions-II25videos
TRIANGLE
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - TRIANGLEEXERCISE - Short Answer Type Questions-II25videos
TRIANGLE
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SURFACE AREA AND VOLUME EXERCISE - PRACTICE TEST ( SECTION-D)1videos
SURFACE AREA AND VOLUME
Similar Questions
Knowledge Check
- Question 1 - Select One or More
In the following figure, XY∣∣QRandPXXQ=PYYR=12 then
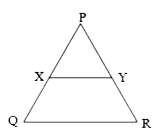 AXY=QRBXY=13QRCXY2=QR2DXY=12QR
AXY=QRBXY=13QRCXY2=QR2DXY=12QR - Question 2 - Select One
In the given figure XY∣∣PQ, find the value of x :
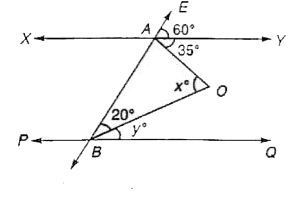 A70∘B40∘C75∘D15∘
A70∘B40∘C75∘D15∘
In the given figure, If QRXY=149andPY=18cm, then what is the value (in cm) of PQ?
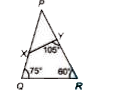 View Solution
View SolutionIn the given figure, if QRXY=149 and PY = 18 cm, then what is the value (in cm) of PQ?
 View Solution
View SolutionIn the given figure , if XY||BC, find the length of XY.
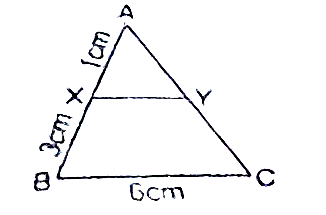 View Solution
View SolutionIn the given figure, QRQS=QTPRand∠1=∠2 then prove that △PQS~△TQR.
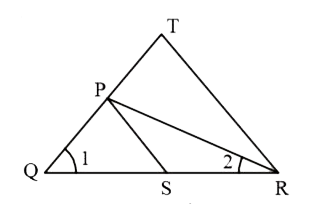 View Solution
View SolutionIf in triangles PQR and XYZ PQXZ=PRXY=QRYZ, then :
View SolutionIn the adjoining figure, MN∣∣QR.
Find (i) PN and (ii) PR.
 View Solution
View Solution


