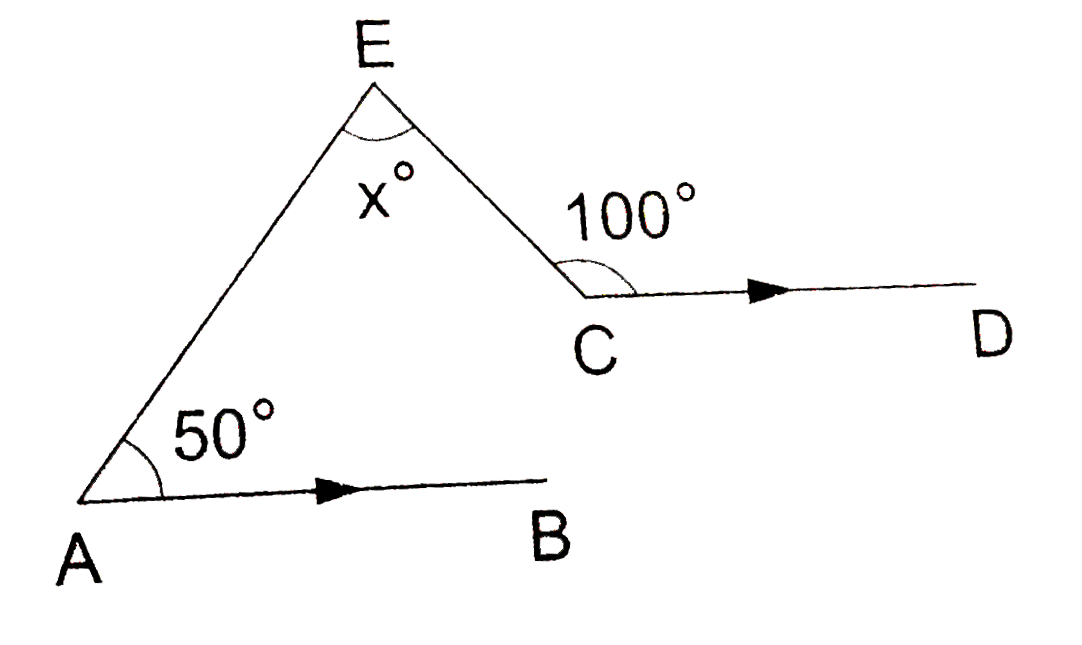
In the given figure,rays OA, OB, OC and OD are such that angleAOB=56^(

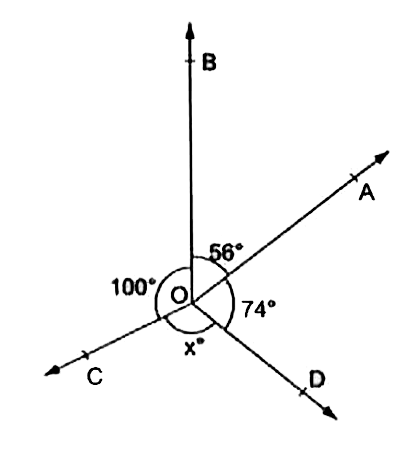
In the given figure, rays OA, OB, OC and OD are such that $∠$ AOB = $50^{\circ}$ , $∠$ BOC = $90^{\circ}$ , $∠ C O D = 70^{\circ}$ and $∠ A O D = x^{\circ}$ . Then, the value of $x$ is
A $50^{\circ}$
B $70^{\circ}$
C $150^{\circ}$
D $90^{\circ}$
In the given figure, $A B ∣ ∣ C D, ∠ A B E = 120^{\circ}, ∠ E C D = 100^{\circ}$ and $∠ B E C = x^{\circ}$ . Find the value of x.

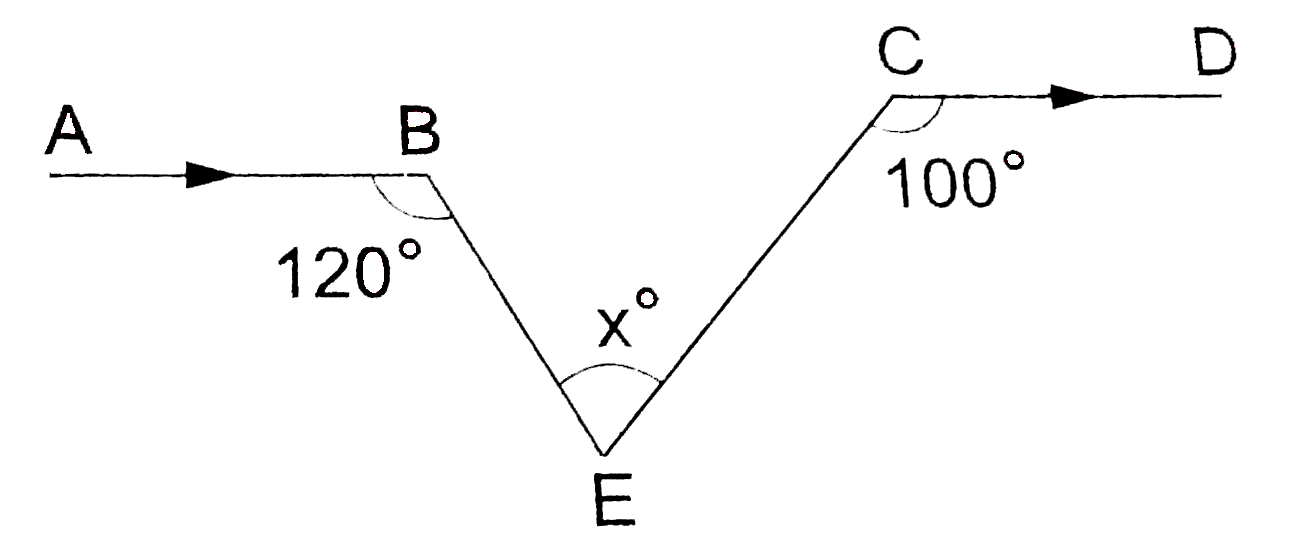A $x = 30$
B $x = 20$
C $x = 50$
D $x = 40$
In the given figure, find the value of $∠ B O C$

A $101^{\circ}$
B $149^{\circ}$
C $71^{\circ}$
D $140^{\circ}$

In the given figure,rays $O A, O B, O C$ and $O D$ are such that $∠ A O B = 56^{\circ}$ , $∠ B O C = 100^{\circ}$ , $∠ C O D = x^{\circ}$ and $∠ D O A = 74^{\circ}$ ,Find the value of $x$ .