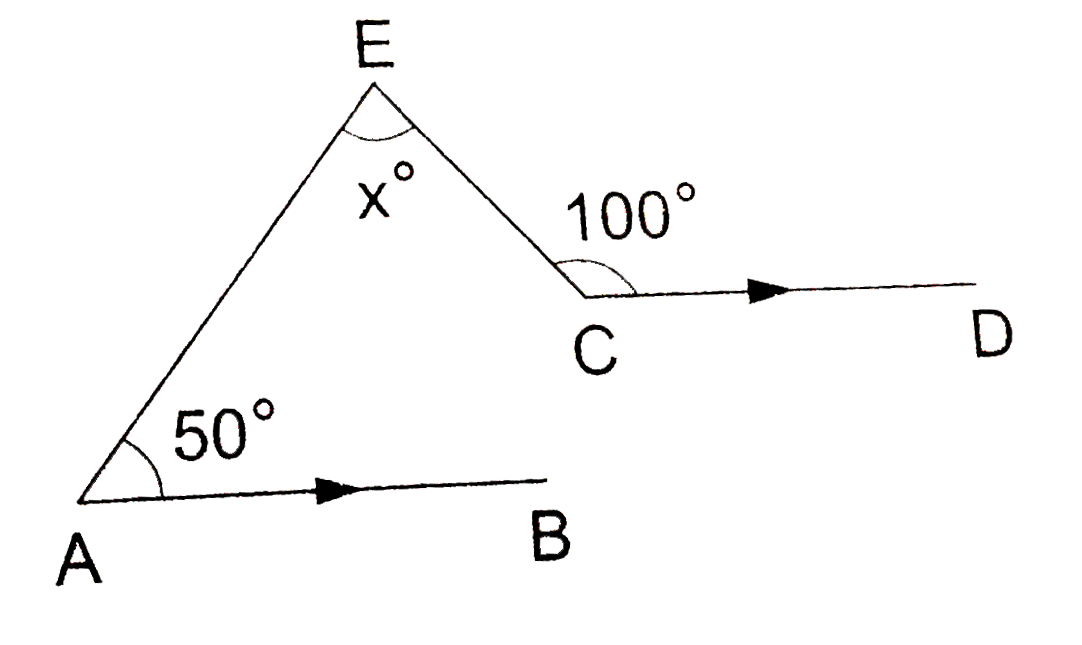
In the given figure, AB∣∣CD,∠BAE=50∘,∠AEC=x∘ and ∠ECD=100∘. Find the value of x.
A
x=70
B
x=60
C
x=50
D
x=40
Video Solution
Text Solution
The correct Answer is:C
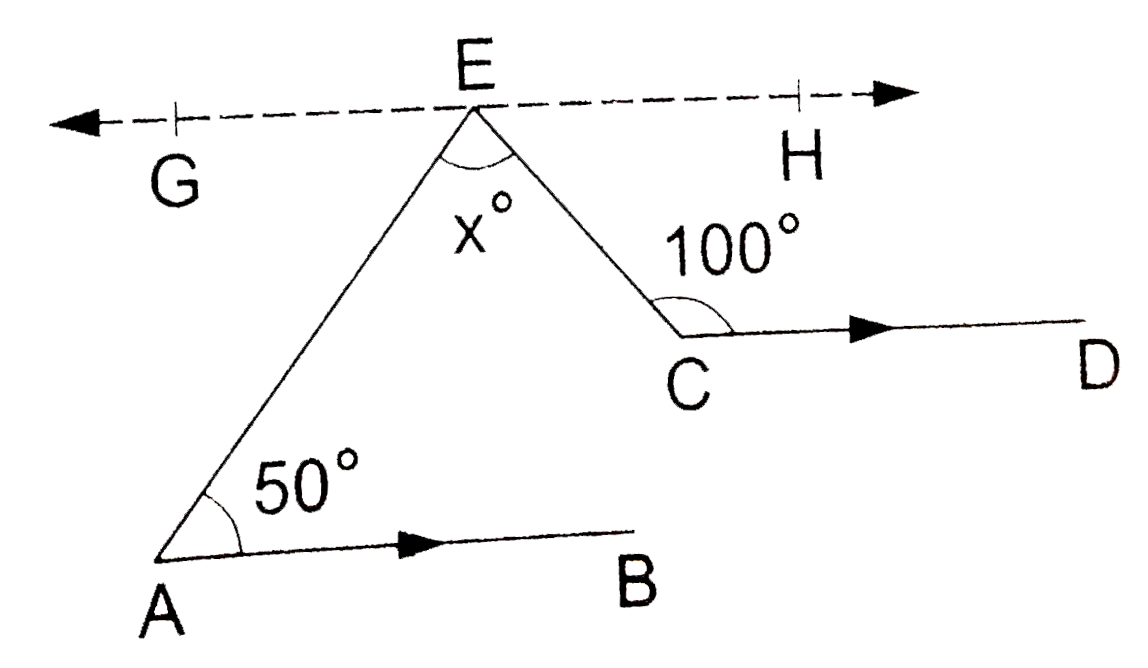
Through E, draw a line GEH||AB||CD.
Now, GE∣∣AB and EA is the transversal.
∴∠GEA=∠EAB=50∘ [alt. int. ∠s].
Again, EH∣∣CD and EC is the transversal.
∴∠HEC+∠ECD=180∘ [co. int. ∠s]
⇒∠HEC+100∘=180∘⇒∠HEC=80∘.
Now, GEH si a straight line.
∴∠GEA+∠AEC+∠HEC=180∘ [staight angle]
⇒50∘+x∘+80∘=180∘⇒x∘=50∘.
Hence, x=50.
|
Topper's Solved these Questions
- LINES AND ANGLESBOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Example
13 Videos
- LINES AND ANGLESBOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Exercise 7A
12 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Multiple Choice Questions (Mcq)
24 Videos
- MEAN , MEDIAN AND MODE OF UNGROUPED DATA BOOK - RS AGGARWALCHAPTER - MEAN , MEDIAN AND MODE OF UNGROUPED DATA EXERCISE - Multiple Choice Questions (Mcq)
18 Videos
Similar Questions
Knowledge Check
In the given figure, AB∣∣CD,∠ABE=120∘,∠ECD=100∘ and ∠BEC=x∘. Find the value of x.
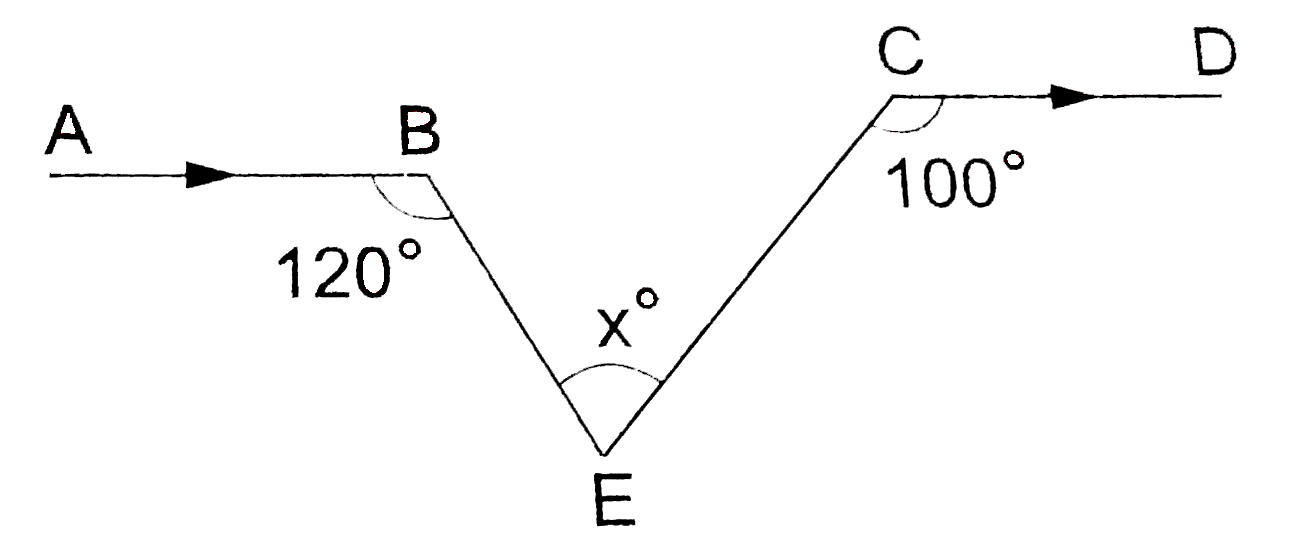 Ax=30Bx=20Cx=50Dx=40
Ax=30Bx=20Cx=50Dx=40In the given figreu AB∣∣CD,∠BAD=30∘and∠ECD=50∘, find ∠CED
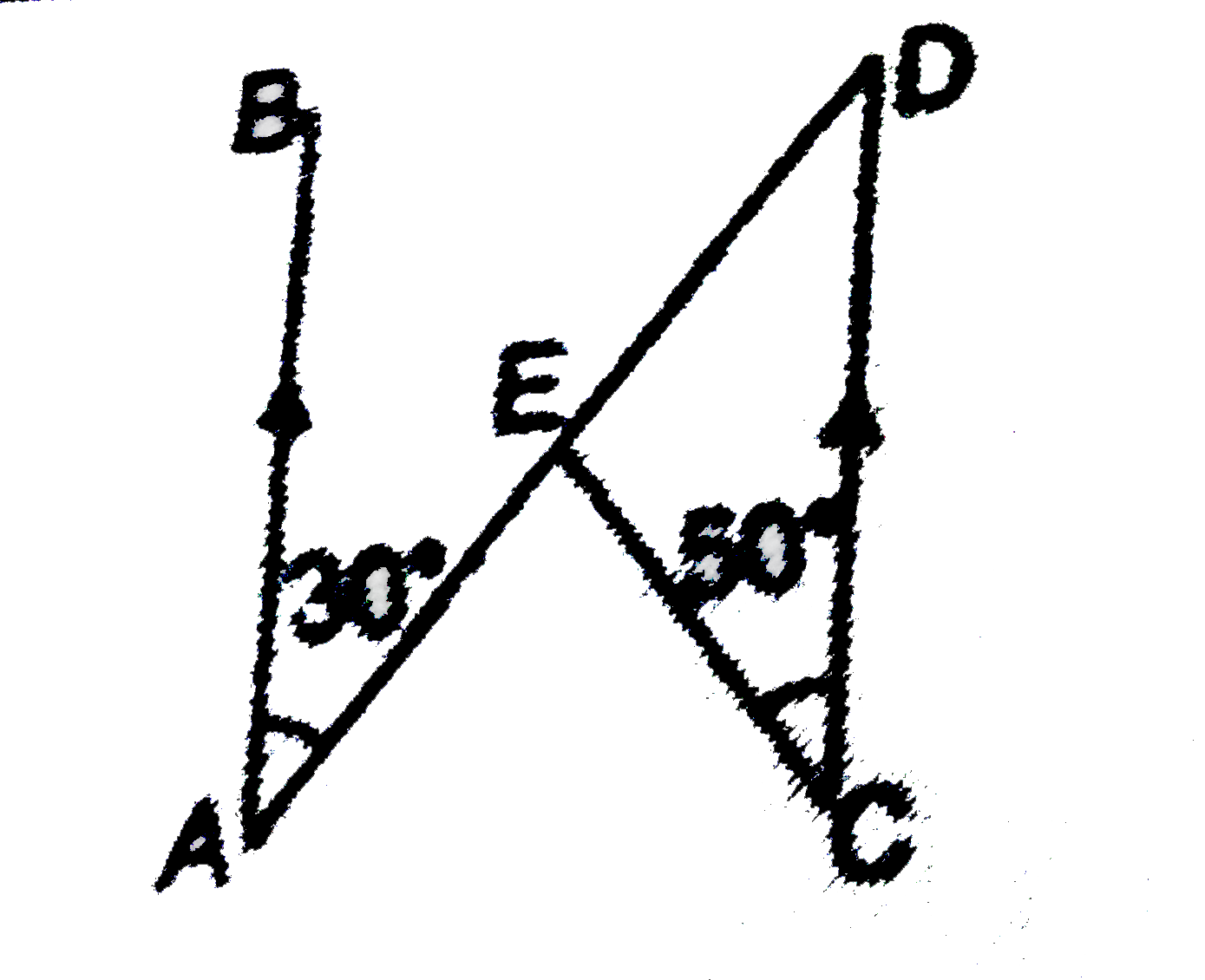 A120∘B30∘C100∘D50∘
A120∘B30∘C100∘D50∘In the given figure , AB∣∣CD. Find x.
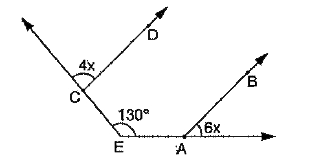 A26∘B13∘C23∘D46∘
A26∘B13∘C23∘D46∘
In the given figure, AB∣∣CD. If ∠EAB=50∘ and ∠ECD=60∘ then ∠AEB=?
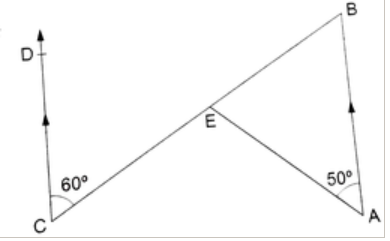
View SolutionIn the figure AB∣∣CD,∠ABE=100∘. Find ∠CDE:

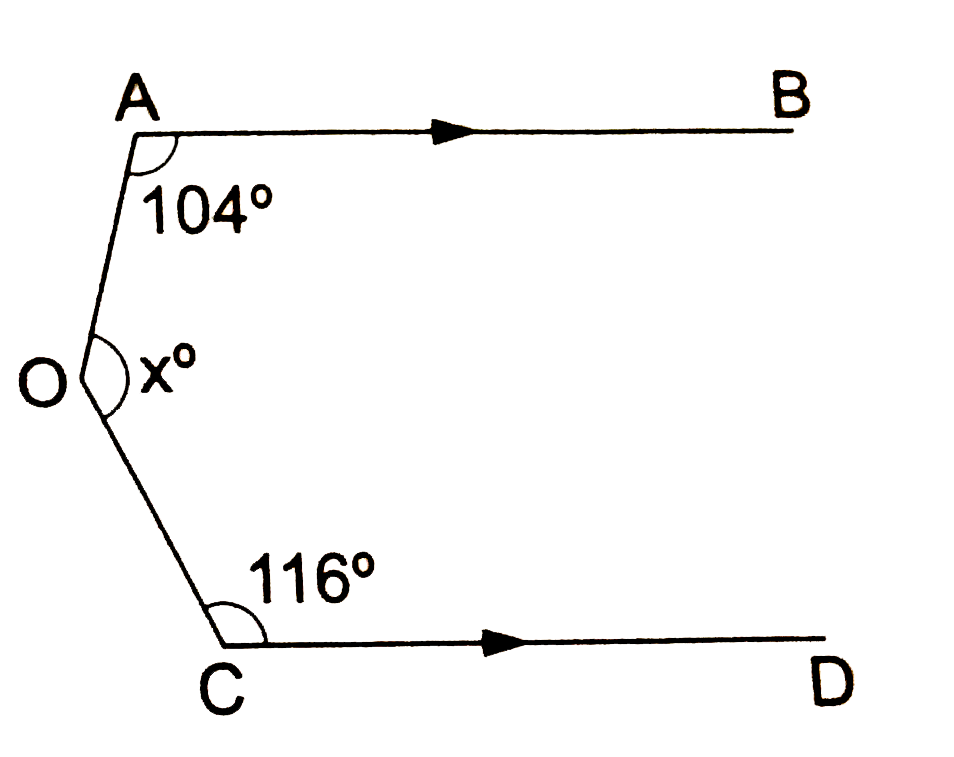
View SolutionIn the given figure, AB∣∣CD. If ∠AOC=30∘ and ∠OAB=100∘ then ∠OCD=?
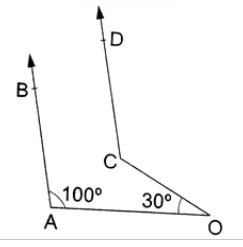
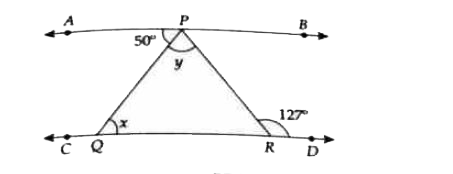
View SolutionIn the given figure if AB||CD ∠APQ=50∘ and ∠PRD=127∘ find x and y.
View SolutionIn the given figure, AB∣∣CD,∠ABO=40∘,∠CDO=35∘. Find the value of the reflex ∠BOD and hence the value of x.
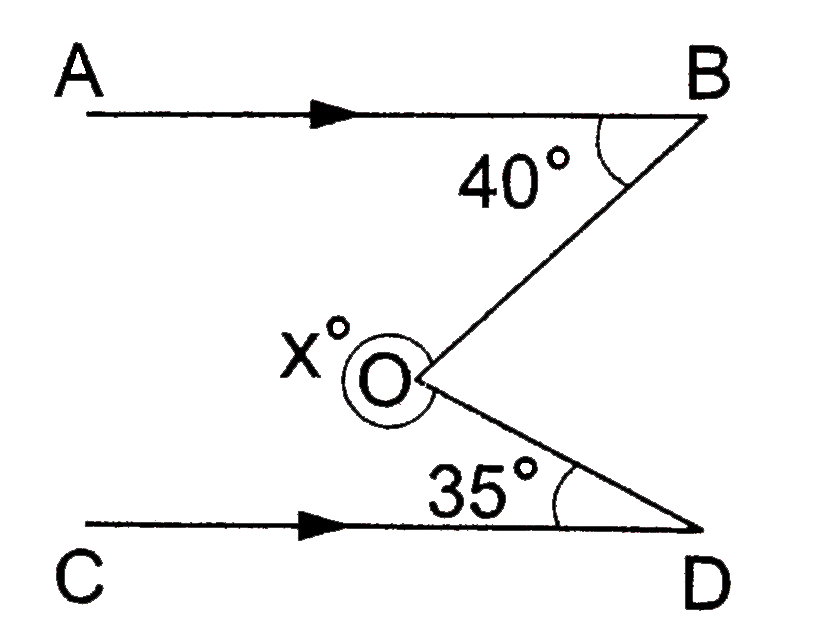
View Solution