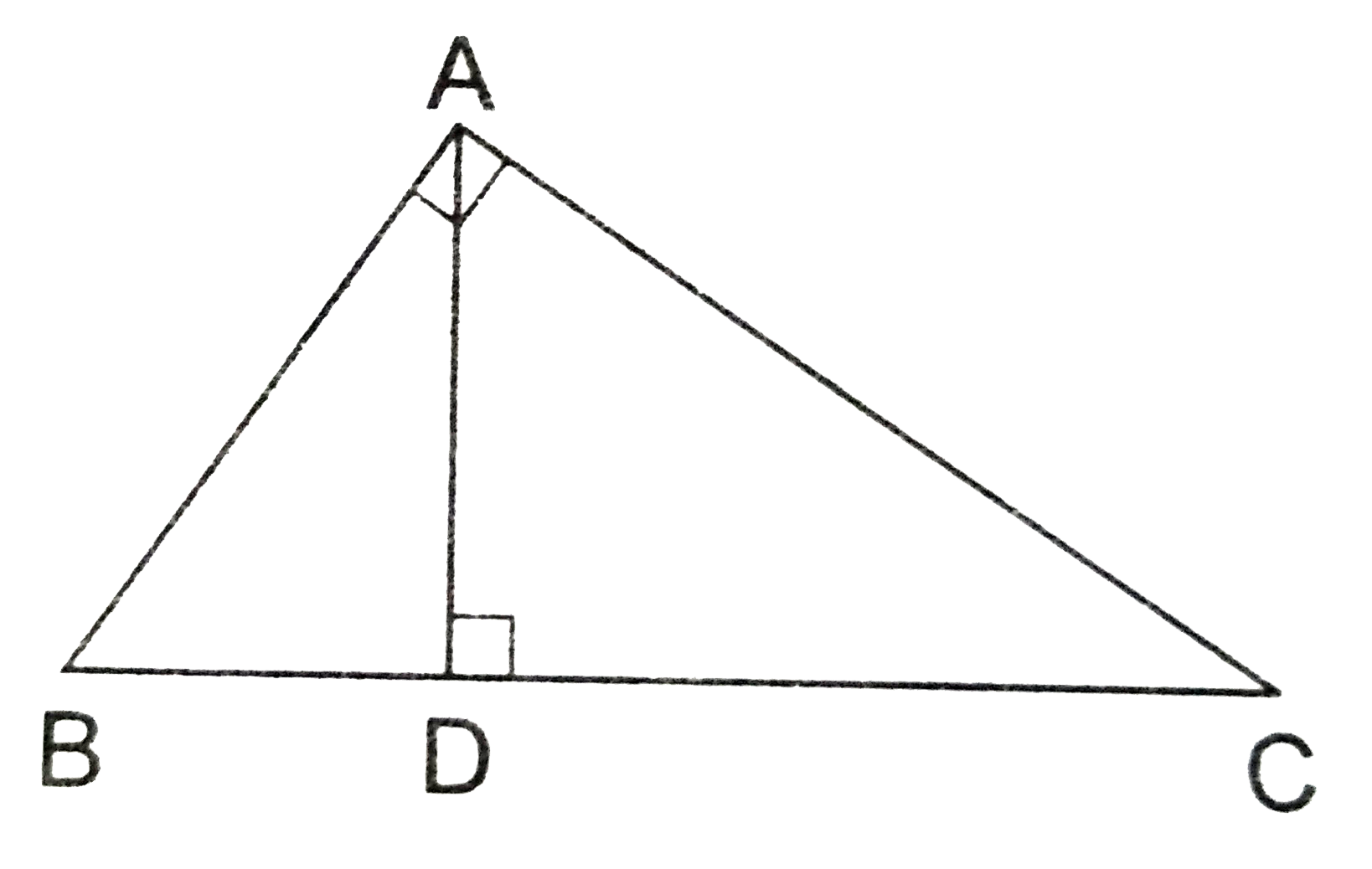
In triangle ABC, ∠BAC=90∘ and AD⊥BC Such that ∠OBA=∠DAC Then:
A
BD.CD=BC2
B
AB.AC=BC2
C
BD.CD=AD2
D
AB.AC=AD2
Text Solution
The correct Answer is:C
|
Topper's Solved these Questions
- SAMPLE PAPER 2BOOK - ICSECHAPTER - SAMPLE PAPER 2EXERCISE - Questions (Section - B)
6 Videos
- SAMPLE PAPER 2BOOK - ICSECHAPTER - SAMPLE PAPER 2EXERCISE - Questions (Section - C)
8 Videos
- SAMPLE PAPER 1BOOK - ICSECHAPTER - SAMPLE PAPER 1EXERCISE - Questions (Section - C)
12 Videos
- SAMPLE PAPER 3BOOK - ICSECHAPTER - SAMPLE PAPER 3EXERCISE - Question (Section -C)
12 Videos
Similar Questions
Knowledge Check
In the figure, if ∠BAC=90∘ and AD⊥BC, then:
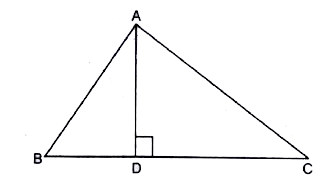 ABD.CD=BC2BAB.AC=BC2CBD.CD=AD2DAB.AC=AD2
ABD.CD=BC2BAB.AC=BC2CBD.CD=AD2DAB.AC=AD2In the figure given below ∠BAC=90∘ and AD ⊥ BC. Then
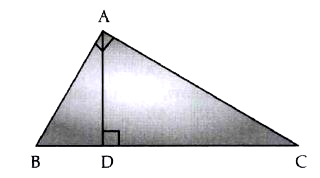 ABC×CD=AC2BAB×AC=BC2CBD×CD=AD2DAB×AC=AD2
ABC×CD=AC2BAB×AC=BC2CBD×CD=AD2DAB×AC=AD2In a △ABC,AB = AC and AD⊥BC, then :
AAB<ADBAB>ADCAB=ADDAB≤AD
In triangle ABC, ∠BAC=90∘andAD⊥BC. If BD = 3 and CD = 4 cm, then the length of AD is.
View SolutionIn △ABC, ∠ABC=90∘ and BD⊥AC. if AD=4 cm and CD=5 cm, then BD is equal to:
△ABC में, ∠ABC=90∘ और BD⊥AC है| यदि AD=4 cm और CD=5 cm तो BD किसके समान होगा?
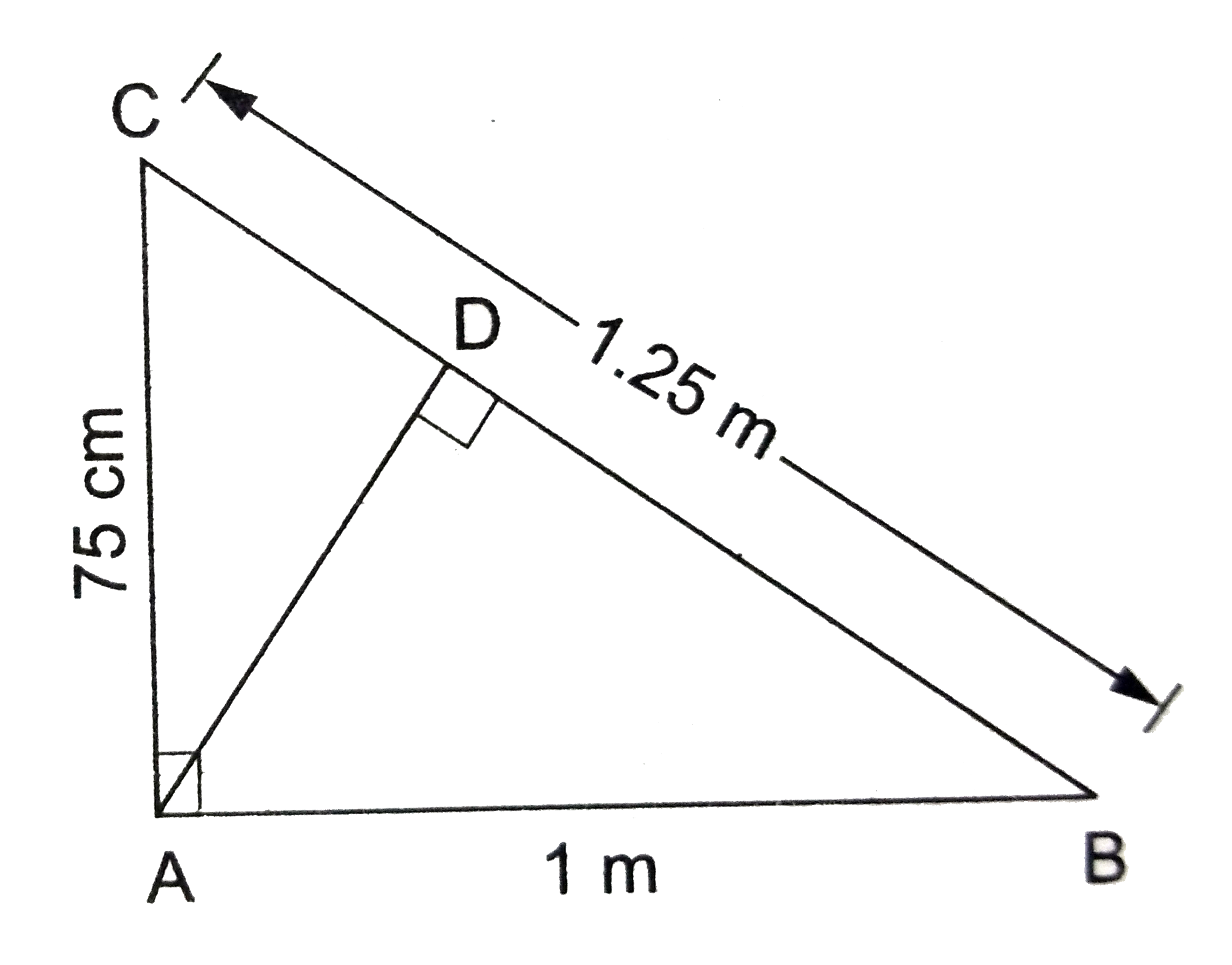
View SolutionIn the given figure, ∠CAB=90∘andAD⊥BC. Show that ΔBDA~ΔBAC. if AC=75cm,AB=1mandBC=1.25cm, find AD.
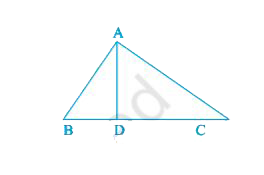
View SolutionIn Fig. 2.12 ∠BAC=90∘ and AD⊥BC.
The number of right triangles in the figure is
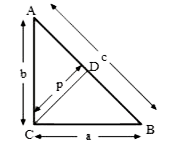
View SolutionIn a right triangle ABC, in which ∠C=90∘amdCD⊥AB. If BC =a, CA=b, AB=c and CD=p, then
View Solution