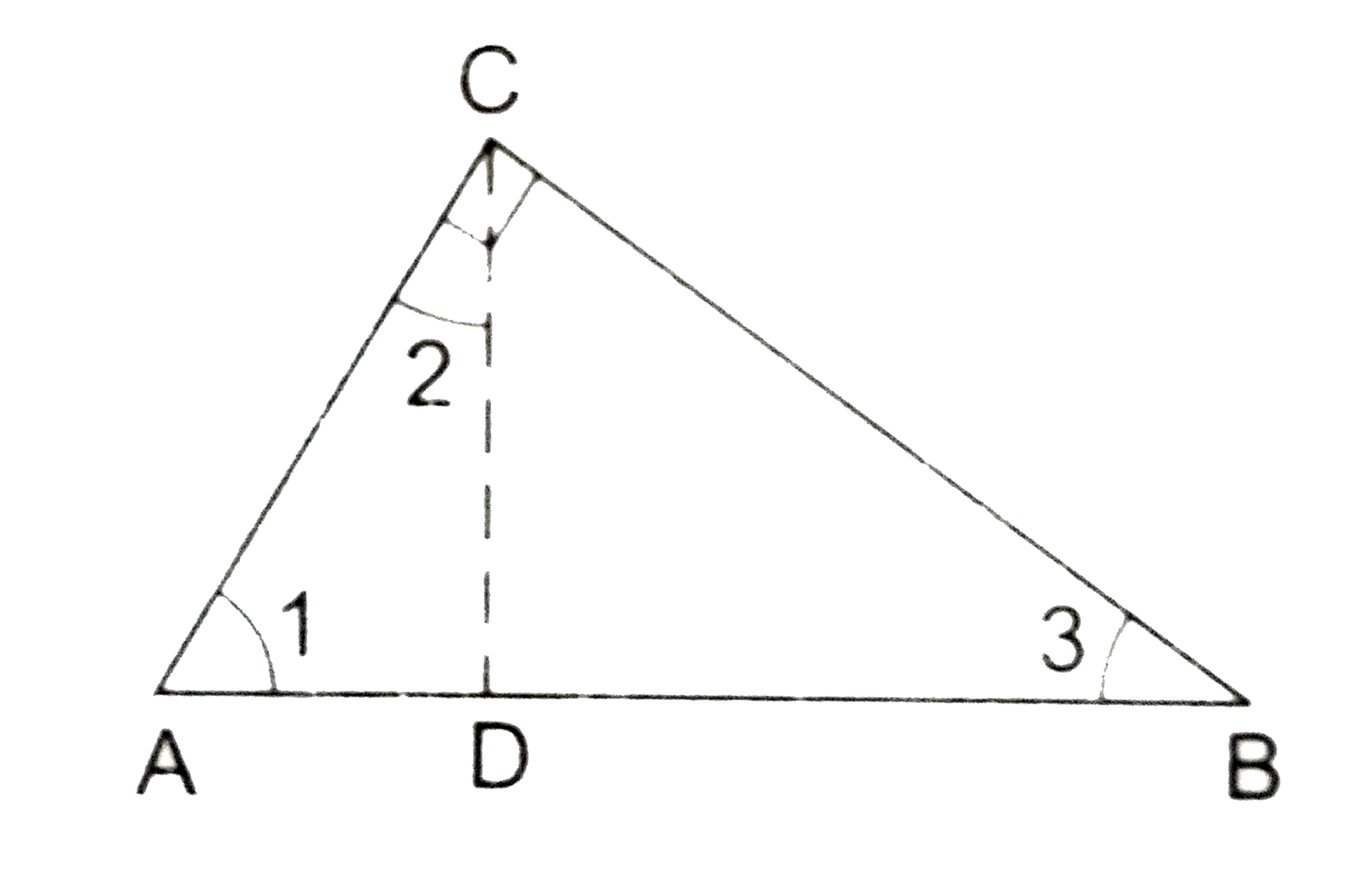
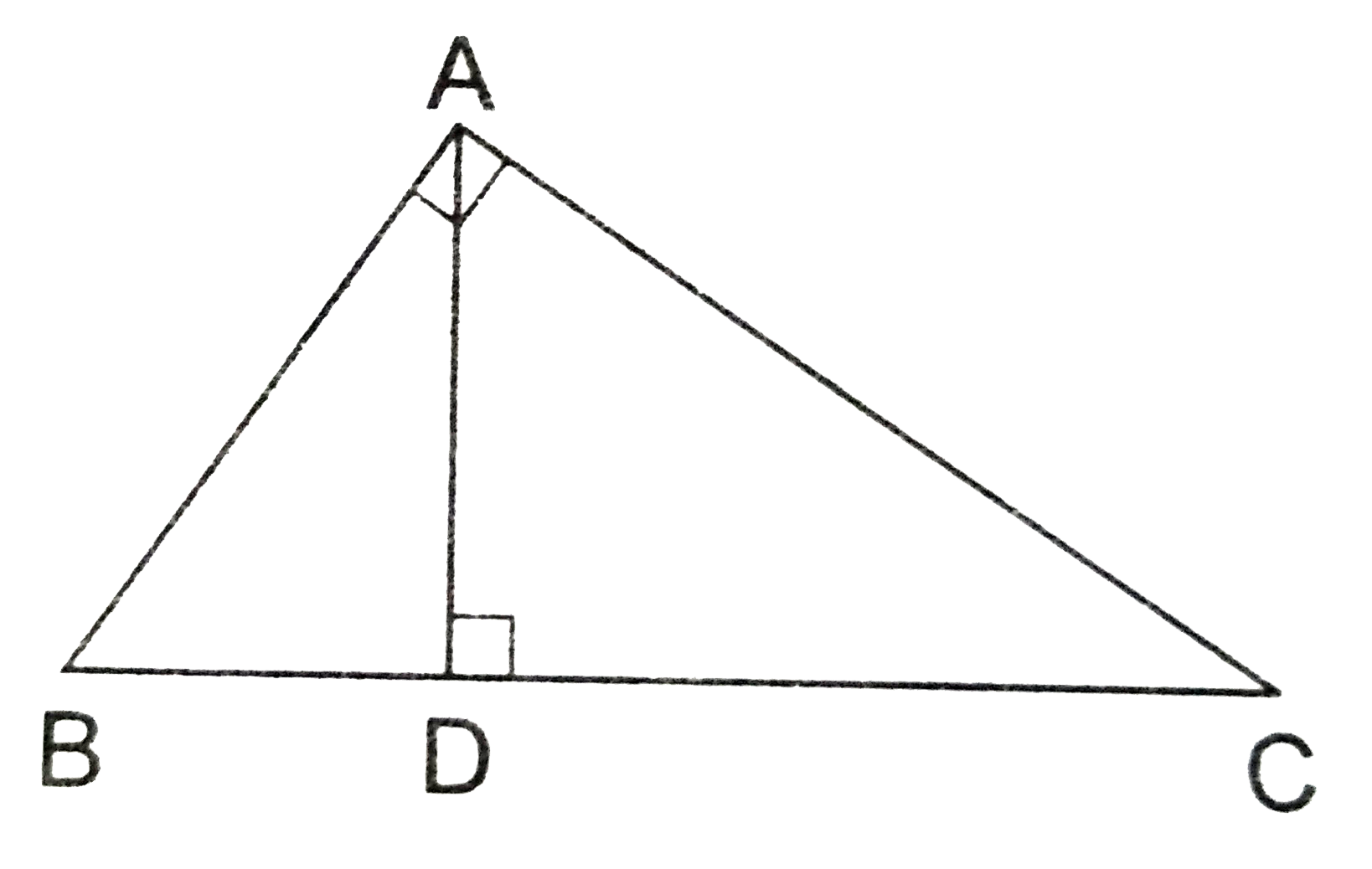
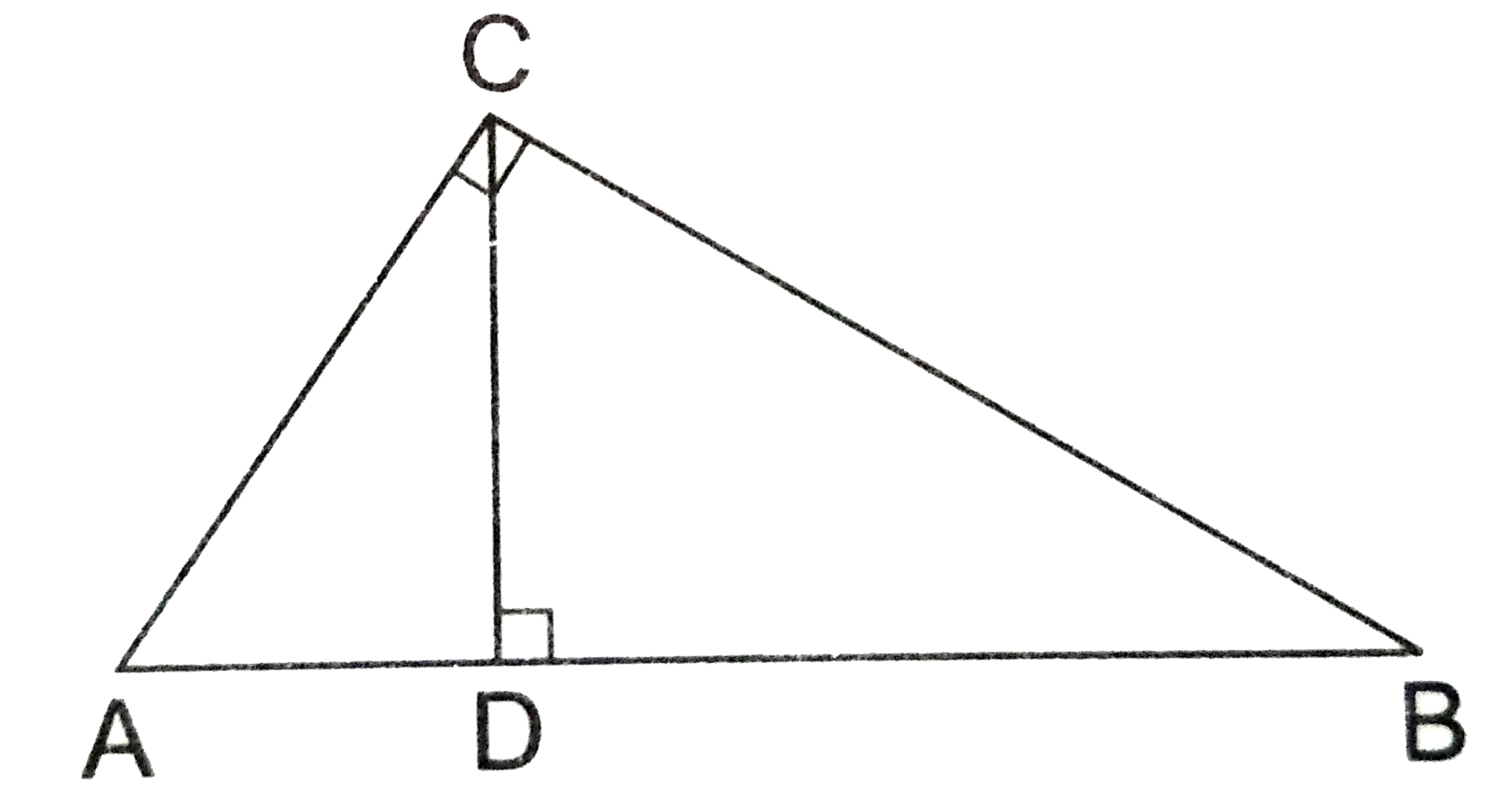
In the given figure, ∠BAC=90∘andAD⊥BC.then,
A
BC⋅CD=BC2
B
AB⋅AC=BC2
C
BD⋅CD=AD2
D
AB⋅AC=AD2
Video Solution
Text Solution
The correct Answer is:C
In ΔDBAandΔDAC, we have
∠ADB=∠CDA=90∘,∠ABD=∠CAD=90∘−∠C
and ∠BAD=∠ACD=90∘−∠B
∴ΔDBA~ΔDAC⇒BDAD=ADCD⇒BD⋅CD=AD2
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTPILE-CHOICE QUESTIONS (MCQ) ( MATCHING OF COLUMNS)1videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Test Yourself20videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7E30videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 1127videos
T-RATIOS OF SOME PARTICULAR ANGLES
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself20videos
TRIGONOMETRIC IDENTITIES
Similar Questions
Knowledge Check
- Question 1 - Select One
In the figure, if ∠BAC=90∘ and AD⊥BC, then:
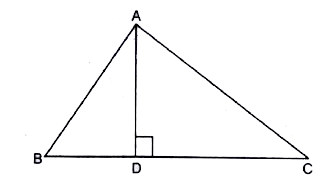 ABD.CD=BC2BAB.AC=BC2CBD.CD=AD2DAB.AC=AD2
ABD.CD=BC2BAB.AC=BC2CBD.CD=AD2DAB.AC=AD2 - Question 2 - Select One
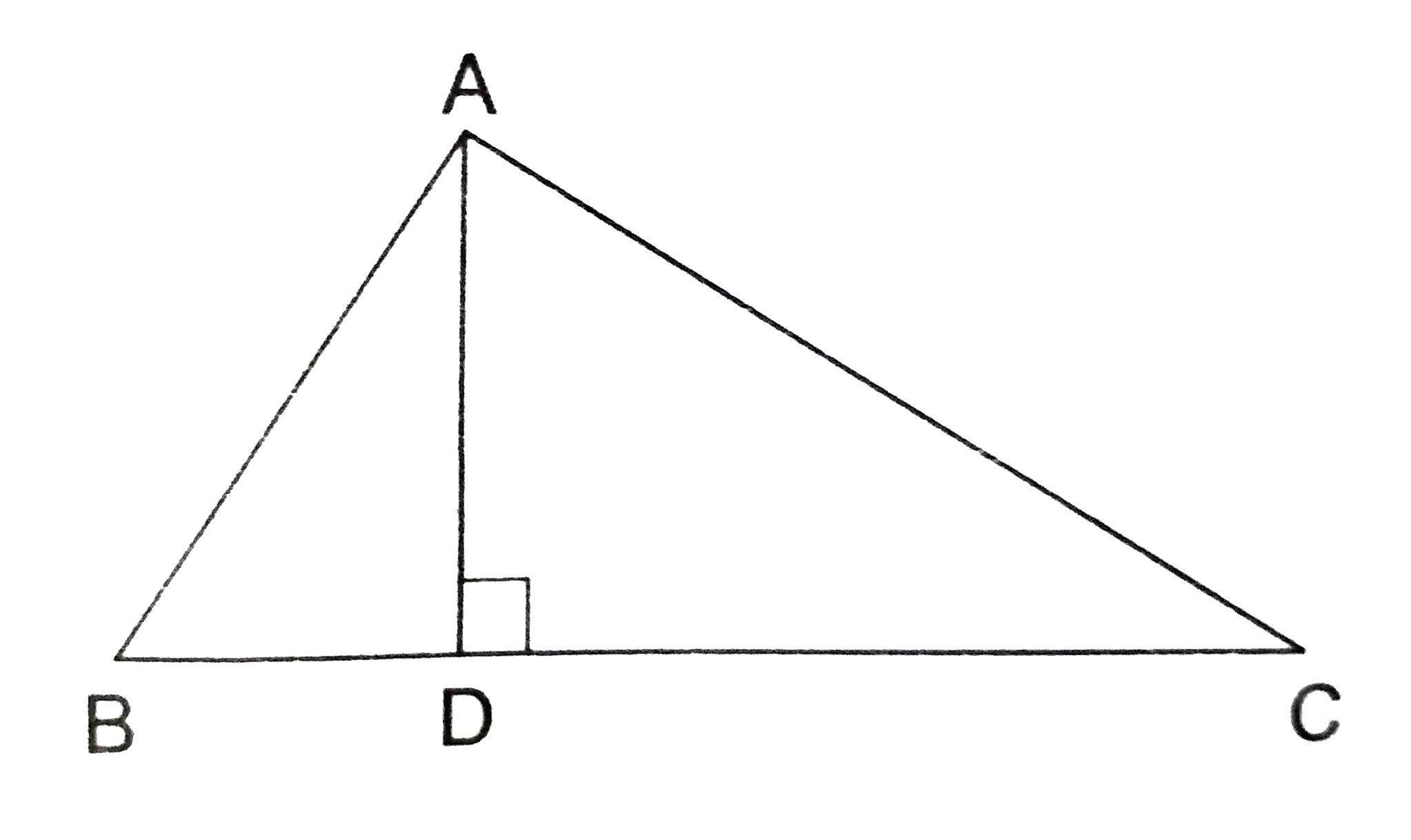
In the figure given below ∠BAC=90∘ and AD ⊥ BC. Then
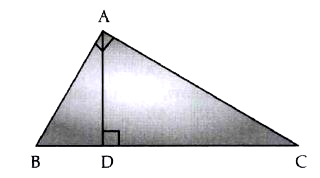 ABC×CD=AC2BAB×AC=BC2CBD×CD=AD2DAB×AC=AD2
ABC×CD=AC2BAB×AC=BC2CBD×CD=AD2DAB×AC=AD2
In the given figure, ∠ABC=90∘andBD⊥AC. If BD=8cm,AD=4cm find CD.
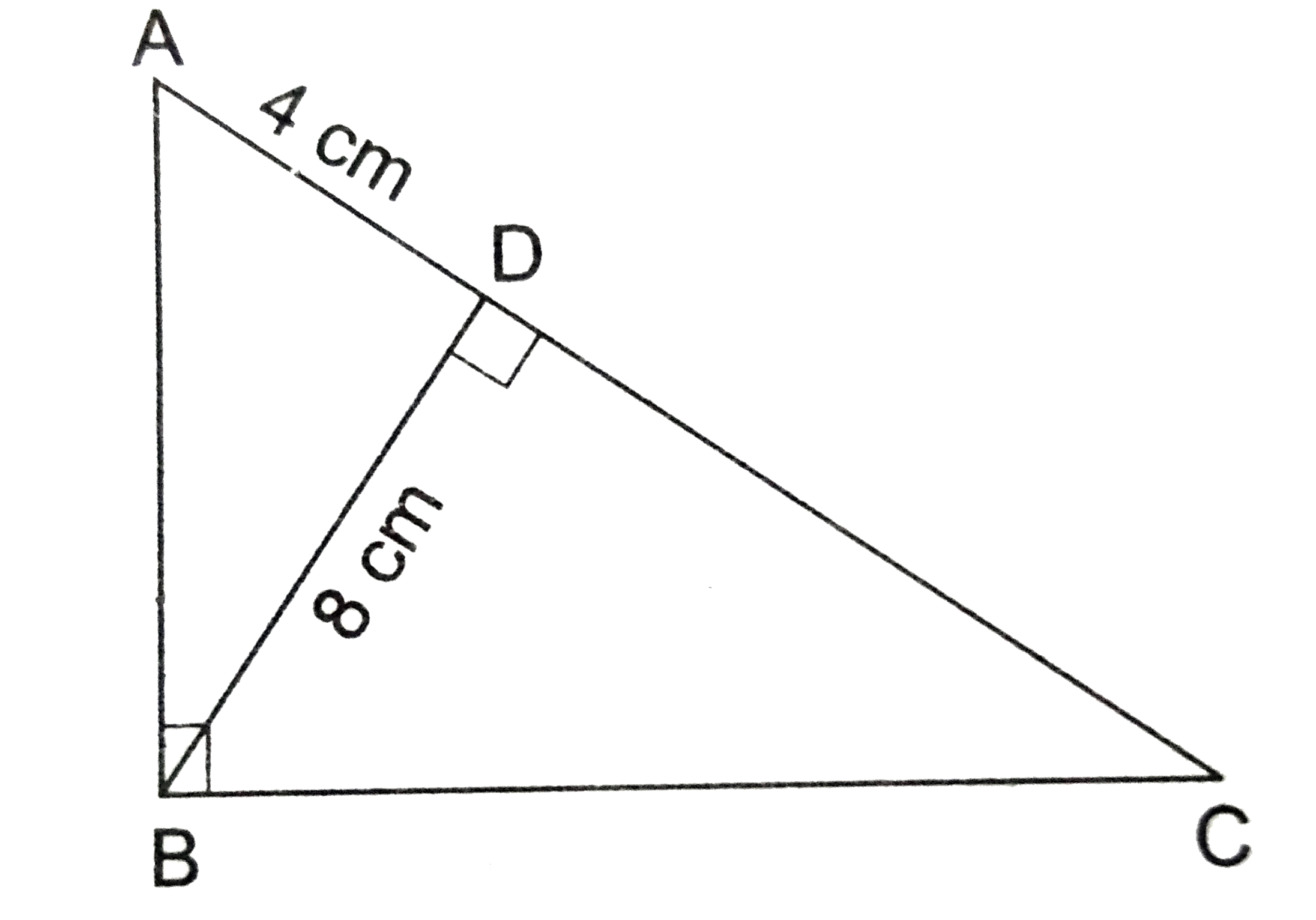 View Solution
View SolutionIn the given figure, ∠ABC=90∘andBD⊥AC. If AB=5.7cm,BD=3.8cmandCD=5.4cm, find BC.
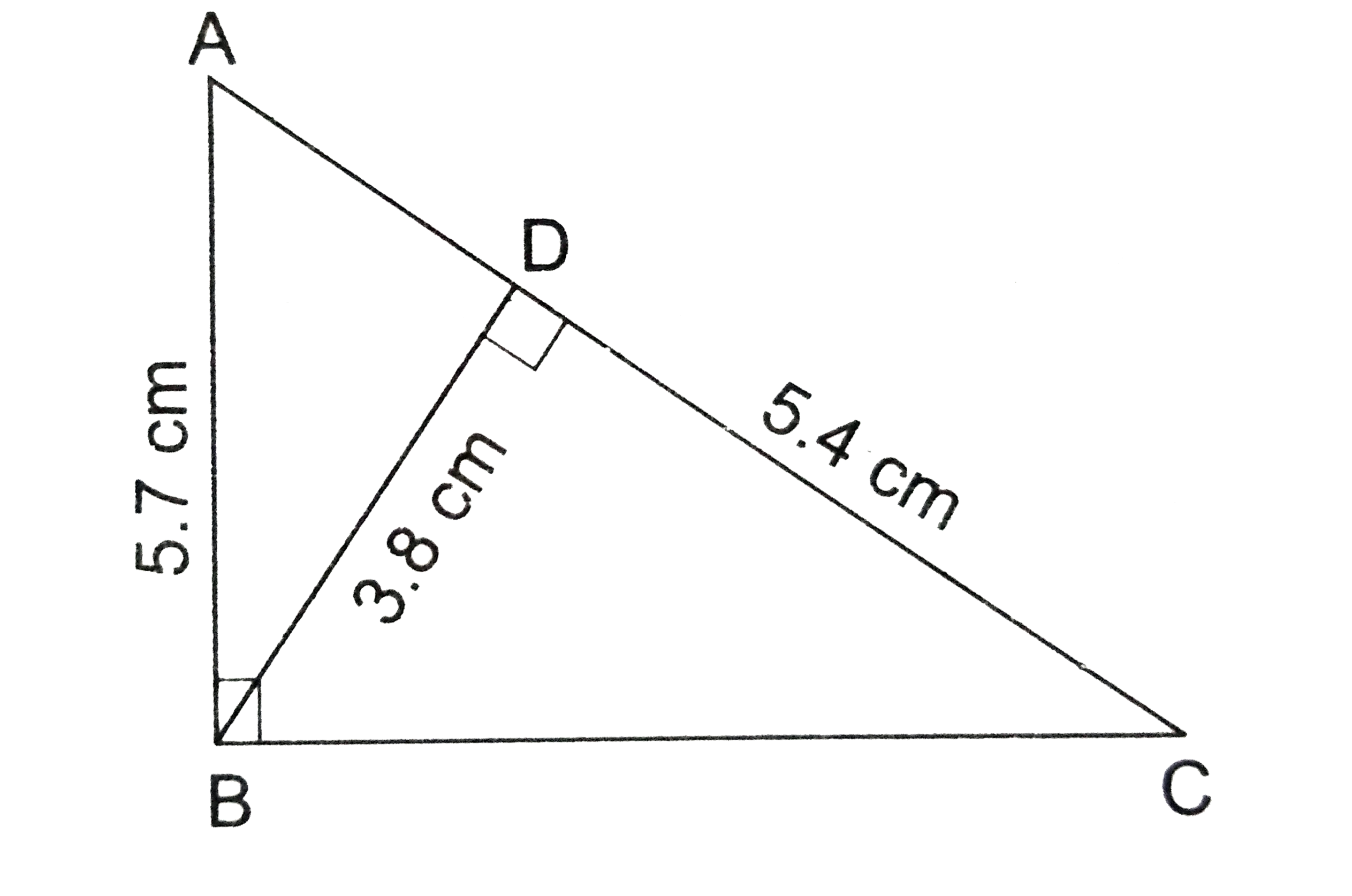 View Solution
View SolutionIn the given figure ∠ABC=90∘andCD⊥AB. Prove that BC2AC2=BDAD
 View Solution
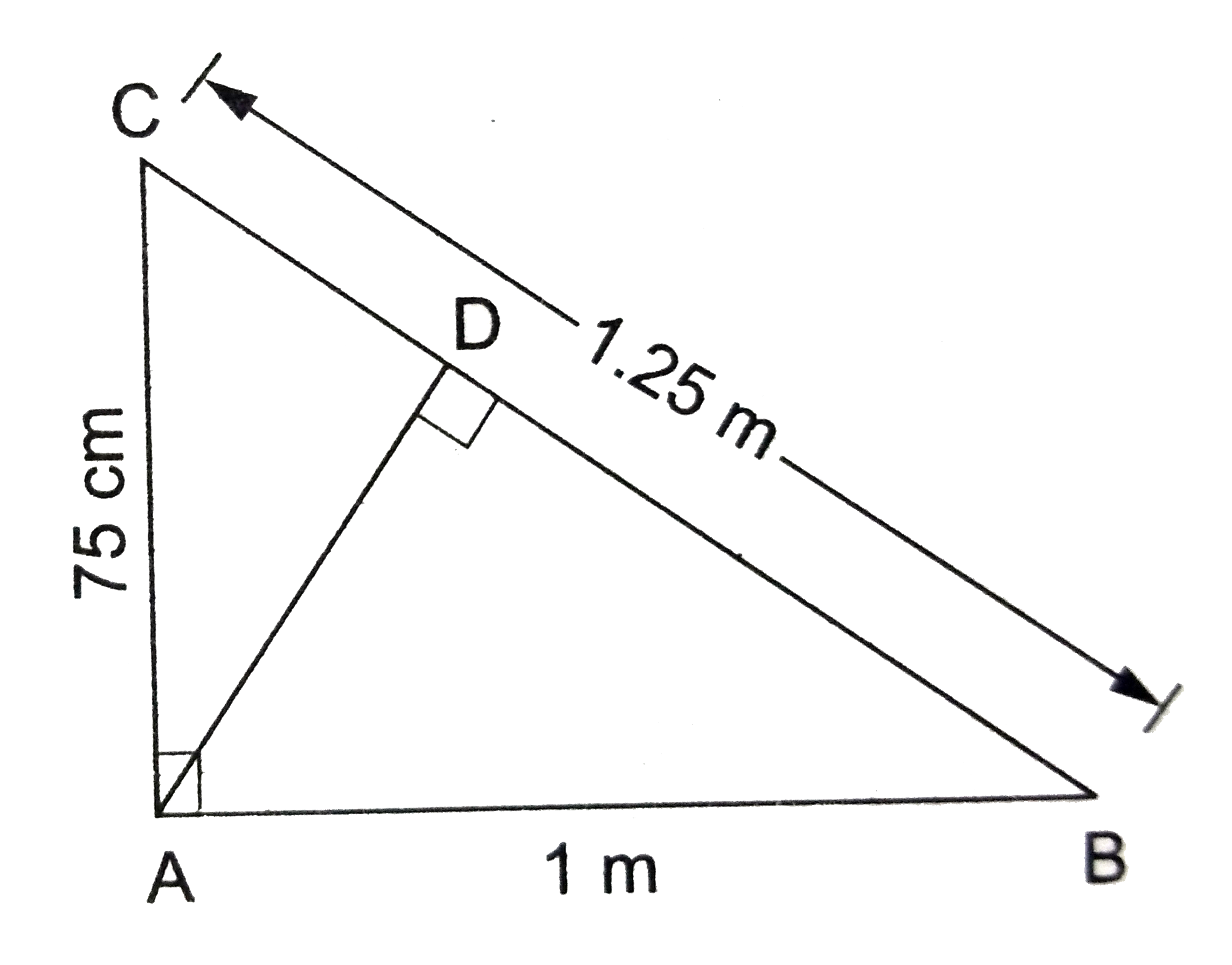
View Solutionin the given figure ∠CAB=90∘andAD⊥BC. if AC= 75 cm , AB= 1m and BD= 1.25 m . Find AD.
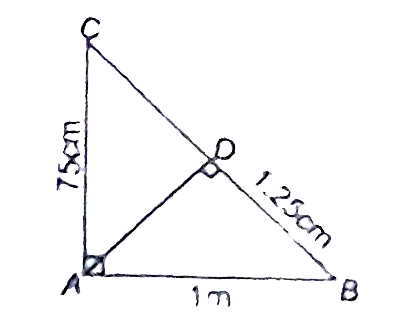 View Solution
View SolutionIn Fig. 2.12 ∠BAC=90∘ and AD⊥BC.
The number of right triangles in the figure is
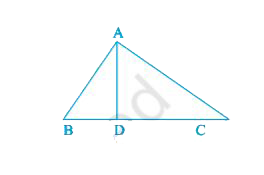 View Solution
View SolutionIn the adjoining figure , ∠B=90∘,∠BAC=θ∘,BC=CD=4cmandAD=10cm, Find (i) sinθand(ii)cosθ.
View Solution