In triangle XYZ, the measure of angle X is 30° greater than the measure of angle Y and angle Z is a right angle. Find the measure of∠Y.
To solve the problem, we need to find the measure of angle Y in triangle XYZ, given that angle X is 30 degrees greater than angle Y and angle Z is a right angle (90 degrees).
1. Identify the Angles:
- Let the measure of angle Y be y.
- Since angle X is 30 degrees greater than angle Y, we can express angle X as:
x=y+30
- Angle Z is given as a right angle:
z=90
2. Use the Triangle Sum Property:
- The sum of the angles in any triangle is always 180 degrees. Therefore, we can write the equation:
x+y+z=180
3. Substitute the Known Values:
- Substitute the expressions for angles X and Z into the equation:
(y+30)+y+90=180
4. Combine Like Terms:
- Combine the terms on the left side:
2y+120=180
5. Isolate y:
- Subtract 120 from both sides:
2y=180−120
2y=60
6. Solve for y:
- Divide both sides by 2:
y=30
Conclusion:
The measure of angle Y is 30∘.
- Let the measure of angle Y be y.
- Since angle X is 30 degrees greater than angle Y, we can express angle X as:
x=y+30
- Angle Z is given as a right angle:
z=90
- The sum of the angles in any triangle is always 180 degrees. Therefore, we can write the equation:
x+y+z=180
- Substitute the expressions for angles X and Z into the equation:
(y+30)+y+90=180
- Combine the terms on the left side:
2y+120=180
- Subtract 120 from both sides:
2y=180−120
2y=60
- Divide both sides by 2:
y=30
The measure of angle Y is 30∘.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Possible measures of three angles of a triangle are
A33∘,42∘,115∘B40∘,70∘,80∘C30∘,60∘,100∘D50∘,60∘,70∘
The measure of a reflex angle is greater than that of a straight angle.
View SolutionWhat is angle; measure of an angle; sense of an angle ; right angle ?
View SolutionFind the measure of each angle of an equilateral triangle.
View Solution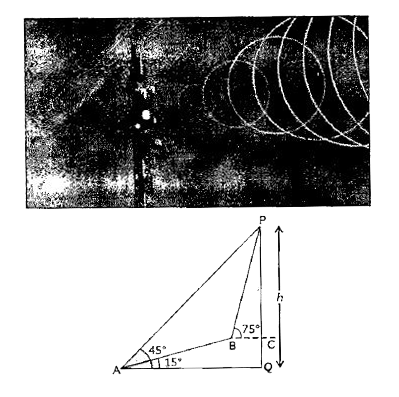
In right angled triangle APQ, the measure of ∠APC is :
View SolutionThe measures of ∠xand∠y in Fig.6.14 are respectively
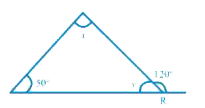
View SolutionThe measure of an angle is twice the measure of its supplementary angle. Find its measure.
View SolutionFind the measure of an angle which is 30∘ less than its supplement.
View Solution
