In △ABC the bisectors of ∠B and ∠C intersect at I if ∠A=70∘ then ∠BIC=…………..
35∘
75∘
100∘
125∘
The correct Answer is:A, B
To find the angle BIC in triangle ABC where the angle bisectors of B and C intersect at point I and given that ∠A=70∘, we can follow these steps:
1. Understand the Triangle Properties:
In any triangle, the sum of the interior angles is 180∘. Therefore, we can write:
∠A+∠B+∠C=180∘
2. Substitute the Given Angle:
We know ∠A=70∘. Substituting this into the equation gives:
70∘+∠B+∠C=180∘
3. Rearrange to Find ∠B+∠C:
To find the sum of angles B and C, we rearrange the equation:
∠B+∠C=180∘−70∘=110∘
4. Use the Angle Bisector Theorem:
The angle bisectors divide the angles into two equal parts. Therefore:
∠IBC=12∠Band∠ICB=12∠C
5. Express ∠BIC:
In triangle BIC, the sum of the angles is also 180∘:
∠IBC+∠ICB+∠BIC=180∘
Substituting the bisector angles gives:
12∠B+12∠C+∠BIC=180∘
6. Substitute the Sum of ∠B+∠C:
We already found that ∠B+∠C=110∘. Thus:
12(110∘)+∠BIC=180∘
Simplifying this:
55∘+∠BIC=180∘
7. Solve for ∠BIC:
Rearranging the equation gives:
∠BIC=180∘−55∘=125∘
Final Answer:
∠BIC=125∘
In any triangle, the sum of the interior angles is 180∘. Therefore, we can write:
∠A+∠B+∠C=180∘
We know ∠A=70∘. Substituting this into the equation gives:
70∘+∠B+∠C=180∘
To find the sum of angles B and C, we rearrange the equation:
∠B+∠C=180∘−70∘=110∘
The angle bisectors divide the angles into two equal parts. Therefore:
∠IBC=12∠Band∠ICB=12∠C
In triangle BIC, the sum of the angles is also 180∘:
∠IBC+∠ICB+∠BIC=180∘
Substituting the bisector angles gives:
12∠B+12∠C+∠BIC=180∘
We already found that ∠B+∠C=110∘. Thus:
12(110∘)+∠BIC=180∘
Simplifying this:
55∘+∠BIC=180∘
Rearranging the equation gives:
∠BIC=180∘−55∘=125∘
∠BIC=125∘
Topper's Solved these Questions
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - SUMS TO ENRICH REMEMBER
9 Videos
- TRIANGLESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIANGLESEXERCISE - SKILL TESTING EXERCISE
19 Videos
- SURFACE AREAS AND VOLUMESBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - MULTIPLE CHOICE QUESTIONS
18 Videos
Similar Questions
Knowledge Check
The internal bisectors of ∠Band∠C of ΔABC meet at O. If ∠A=80∘ then ∠BOC is :
A50∘B160∘C100∘D130∘In a triangle ABC , OB and OC are the bisector of angle ∠B and ∠C respectively . ∠BAC=60∘ . The angle ∠BOC will be :
A150∘B120∘C100∘D90∘In the adjacent figure, the bisectors of ∠Aand∠B meet in a point P. If ∠C=100∘and∠D=60∘, find the measure of ∠APB.
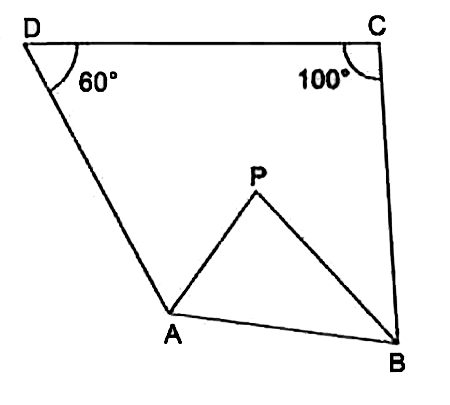 A80∘B100∘C70∘D60∘
A80∘B100∘C70∘D60∘
In △ABC,∠A=40∘ if bisector of ∠B and ∠C meets at O then prove that ∠BOC=110∘
View SolutionBO and CO are external bisector of ∠B and ∠C of △ABC intersecting at O. If internal bisector of ∠B and ∠C intersect at P, prove that ∠PBO=90∘ and ∠BOC+∠BPC=180∘
View SolutionIn a parallelogram ABCD, the bisectors of ∠Aand∠B intersect each other at point P. Prove that ∠APB=90∘.
View SolutionIn ΔABC, bisectors of ∠Band∠C interesct each other at point O. Prove that ∠BOC=90∘+12∠Ai.e.,∠1=90∘+12
View SolutionABC is a triangle. The bisectors of the internal angle ∠B and external angle ∠C Intersect at D. If ∠BDC=50∘, then ∠A is
View Solution
