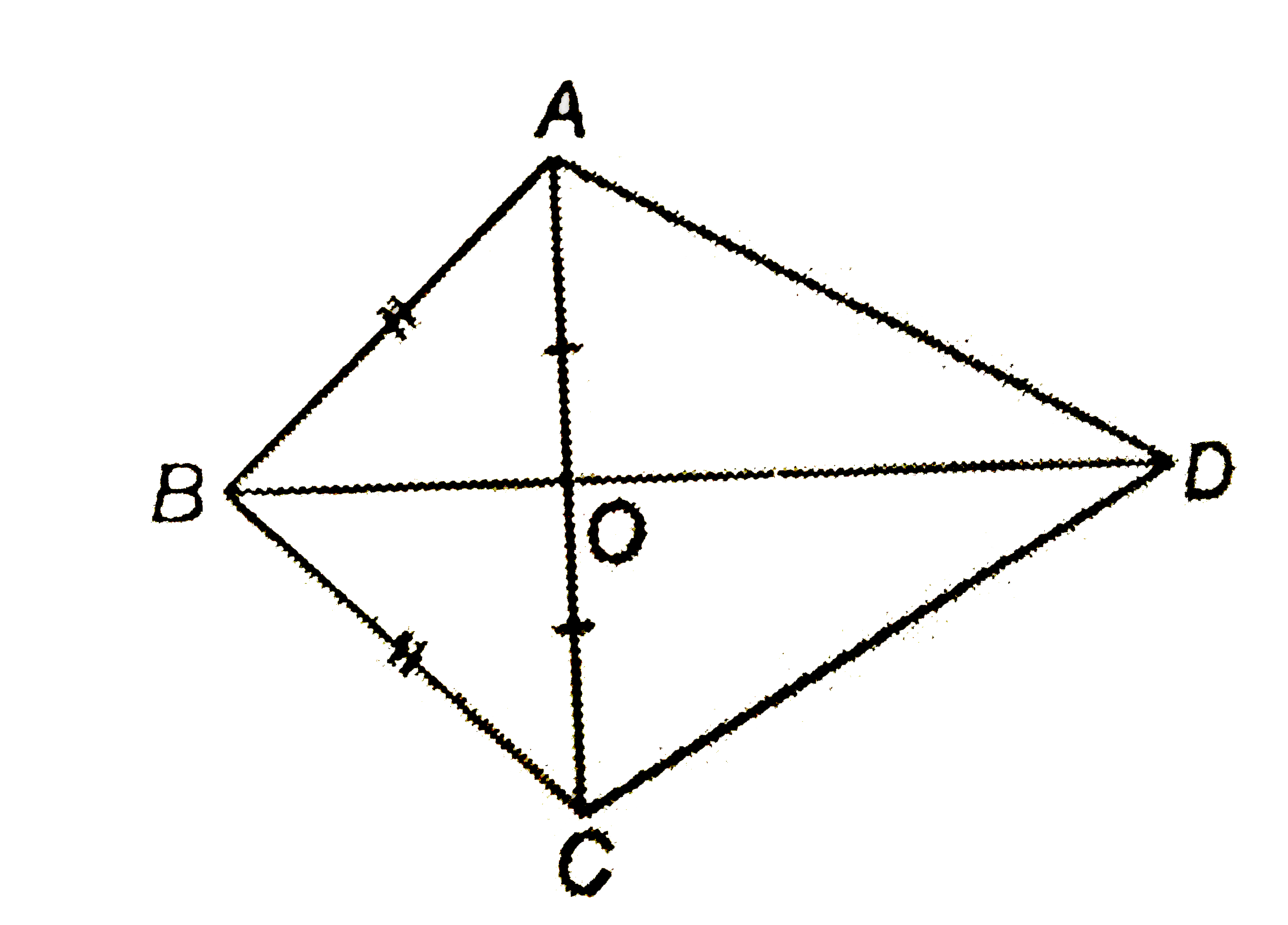
In the given figure, OA = OB and OD = OC. Show that
(i) ΔAOD≅ΔBOC and (ii) AD∣∣BC
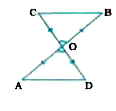
The correct Answer is:AD||BC
Step by step video & image solution for In the given figure, OA = OB and OD = OC. Show that (i) DeltaAOD cong DeltaBOC and (ii) AD||BC by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
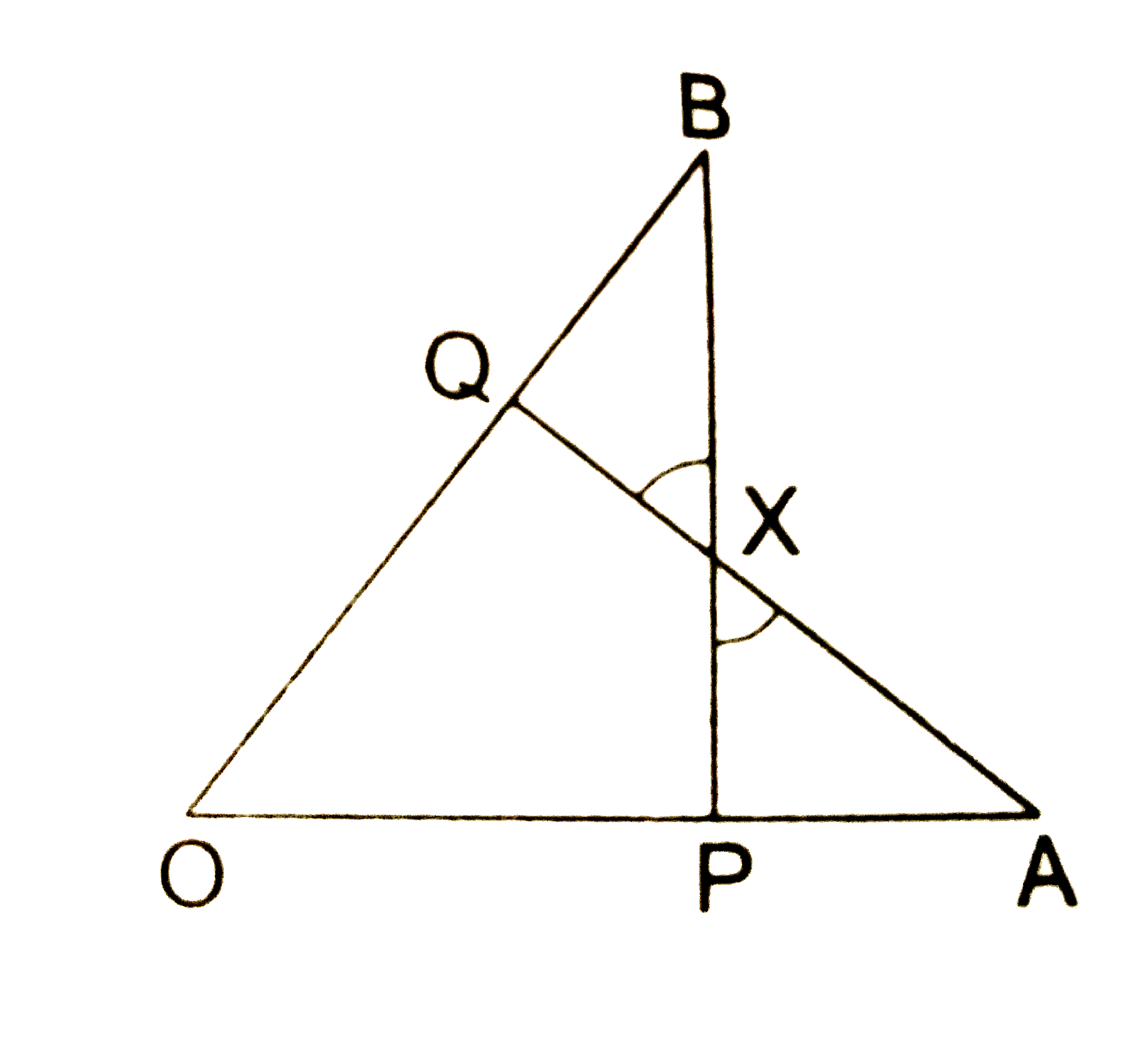
In the given figure, OA=OB and OP=OQ. Prove that (i) PX=QX, (ii) AX=BX
View SolutionIn the given figure, AD⊥BCandCD>BD. Show that AC>AB.

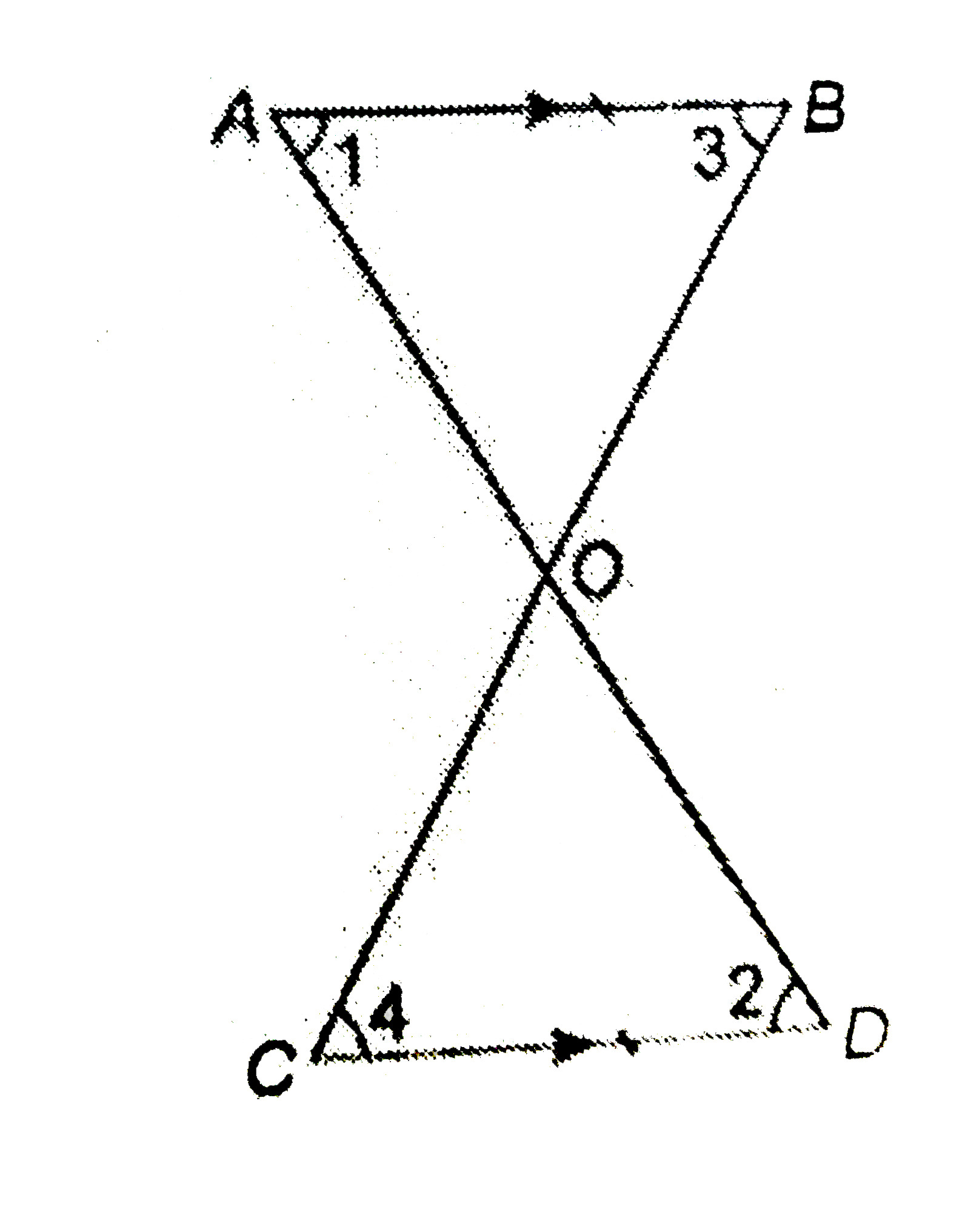
View SolutionIn the adjoining figure, AB = CD and AB||CD prove that
(i) ΔAOB≅ΔDOC
(ii) AD and BC bisect each other at the point O.
View SolutionIn the givne figure, OA = OB and OP = OQ.
Prove that (i) PX = QX, (ii) AX = BX.
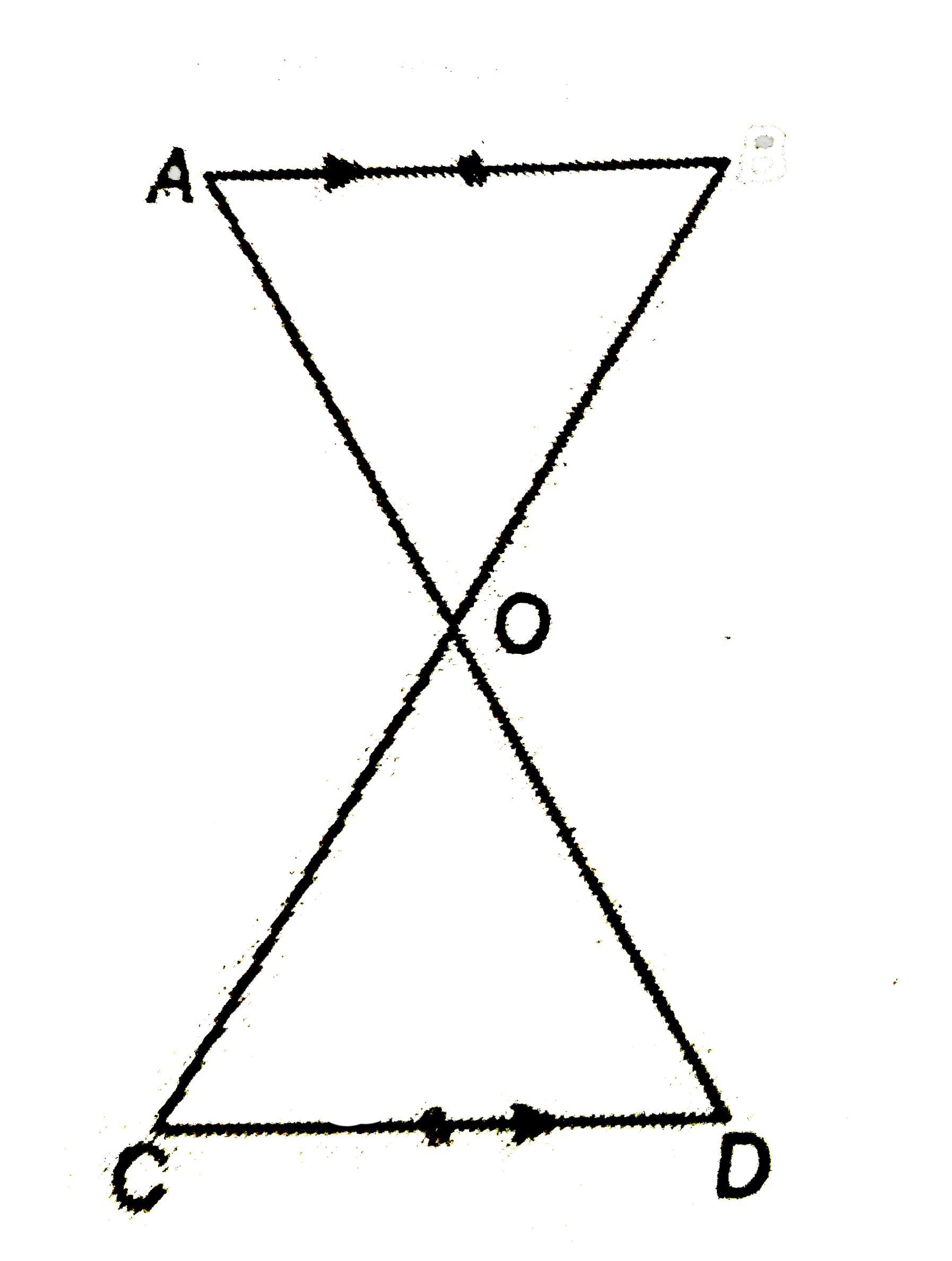
View SolutionIn the adjoining figure AB=CD and AB||CD prove that :
(i) ΔAOB≅ΔDOG
(ii) AD and BC bisect each other at point O.
View SolutionIn the given figure, Oa = OB and OC = OD. Which is the criteria to prove
ΔAOC≅ΔBOD.

View SolutionIn the given figure, AB||CDandO is the midpoint of AD.
Show that (i) ΔAOB≅ΔDOC.
(ii) O is the midpoint of BC.

View SolutionIn the given figure, ∠B<∠Aand∠C<∠D. Show that AD<BC.
View SolutionIn the following figure, OA = OC and AB = BC. Prove that :
(i) ∠APB=90∘
(ii) ΔAOD≅ΔCOD
(iii) AD=CD
View SolutionIn figure OA∗OB=OC∗OD. Show that ∠A=∠Cand ∠B=∠D.
View Solution
