Inscribed Angle Theorem
The measure of an inscribed angle is half of the measure of the arc intercepted by it.
Given : In a circle with centre O, ∠BAC is inscribed in an arc BAC. ∠BAC intercepts are BXC of the circle.
To prove :m∠BAC=12 m ( arc BXC ) .
Step by step video solution for Inscribed Angle Theorem The measure of an inscribed angle is half of the measure of the arc intercepted by it. Given : In a circle with centre O, /_BAC is inscribed in an arc BAC. /_BAC intercepts are BXC of the circle. To prove : m /_BAC = (1)/(2) m ( arc BXC ) . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- BOARD QUESTION PAPER: MARCH 2019BOOK - TARGET PUBLICATIONCHAPTER - BOARD QUESTION PAPER: MARCH 2019EXERCISE - (B) (Solve the following questions (Any two):
3 Videos
- BOARD QUESTION PAPER: MARCH 2019BOOK - TARGET PUBLICATIONCHAPTER - BOARD QUESTION PAPER: MARCH 2019EXERCISE - (Solve the following questions (Any three):
4 Videos
- BOARD QUESTION PAPER: MARCH 2019BOOK - TARGET PUBLICATIONCHAPTER - BOARD QUESTION PAPER: MARCH 2019EXERCISE - (B) (Solve the following questions (Any Two) :
3 Videos
- ARITHMETIC PROGRESSION BOOK - TARGET PUBLICATIONCHAPTER - ARITHMETIC PROGRESSION EXERCISE - Chapter Assessment
17 Videos
- CHALLENGING QUESTIONS BOOK - TARGET PUBLICATIONCHAPTER - CHALLENGING QUESTIONS EXERCISE - Chapter 6: Statistics
4 Videos
Similar Questions
Corollaries of inscribed angle theorem :
Angle inscribed in the same arc arc contruent
Given : (1) A circle with centre O
(2) ∠ABD and ∠ACD are inscribed in arc ABC and intercepts arc APD.
To prove : ∠ABD≅∠ACD
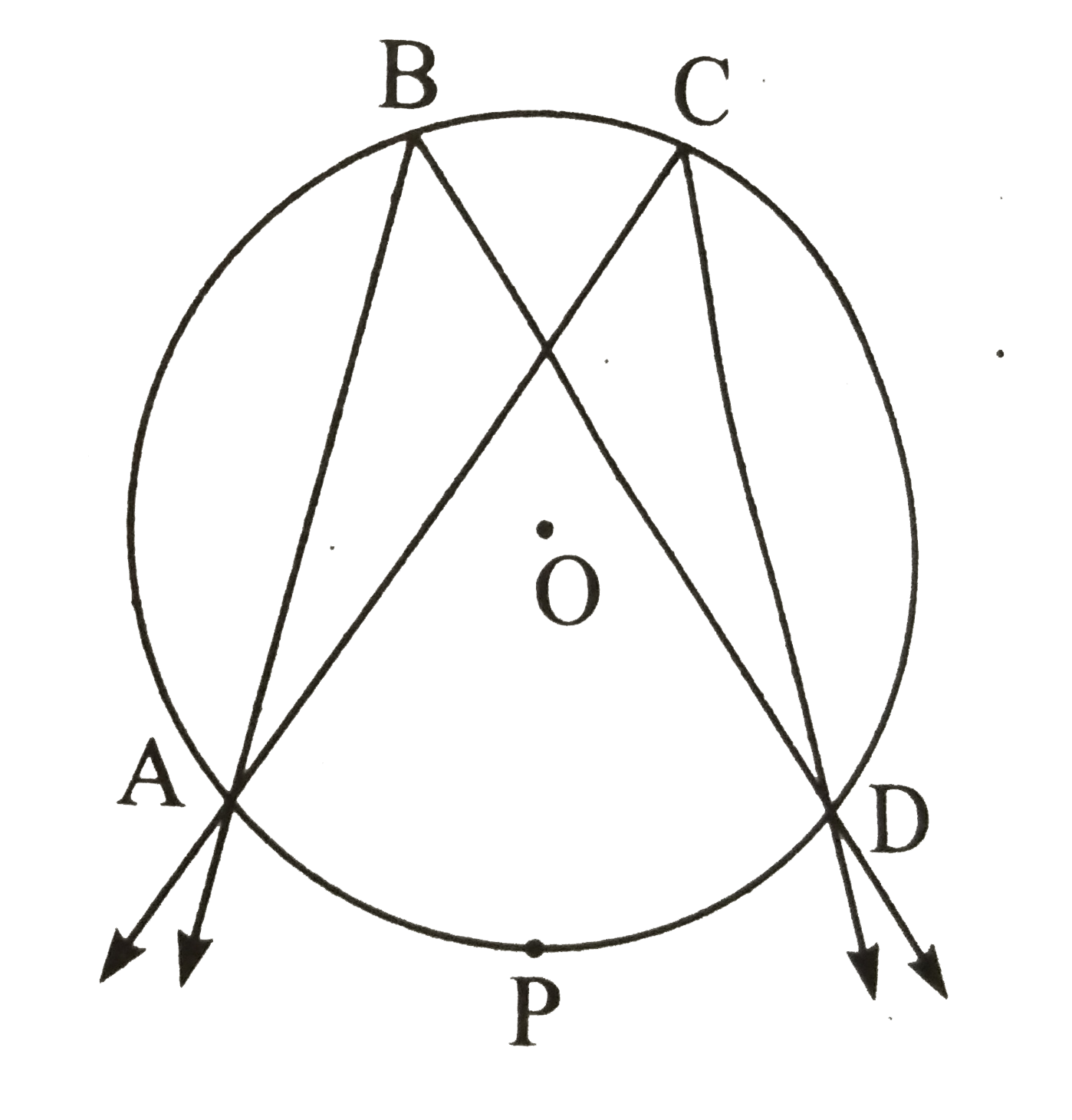
View SolutionIn the figure, O is the centre of the circle. Seg AC is the diameter ∠ABC is inscribed in arc ABC and intercepts arc AMC then prove ∠ABC=90∘

View Solution
Knowledge Check
∠ACB is inscribed in arc ACB of a circle with centre O . If ∠ACB=65∘ , find m ( arc ACB ) .
A65∘B130∘C295∘D230∘The radian measure of the angle, subtends at the centre of a circle by an arc whose length is twice the diameter of the circle, is
A2Bπ2CπD4
Theorem of angle between tangent and secant
If an angle has its vertex on the circle, its one side touches the circle and the other intersects the circle in one more point, then the measure of the angle is half the measure of its intercepted arc .
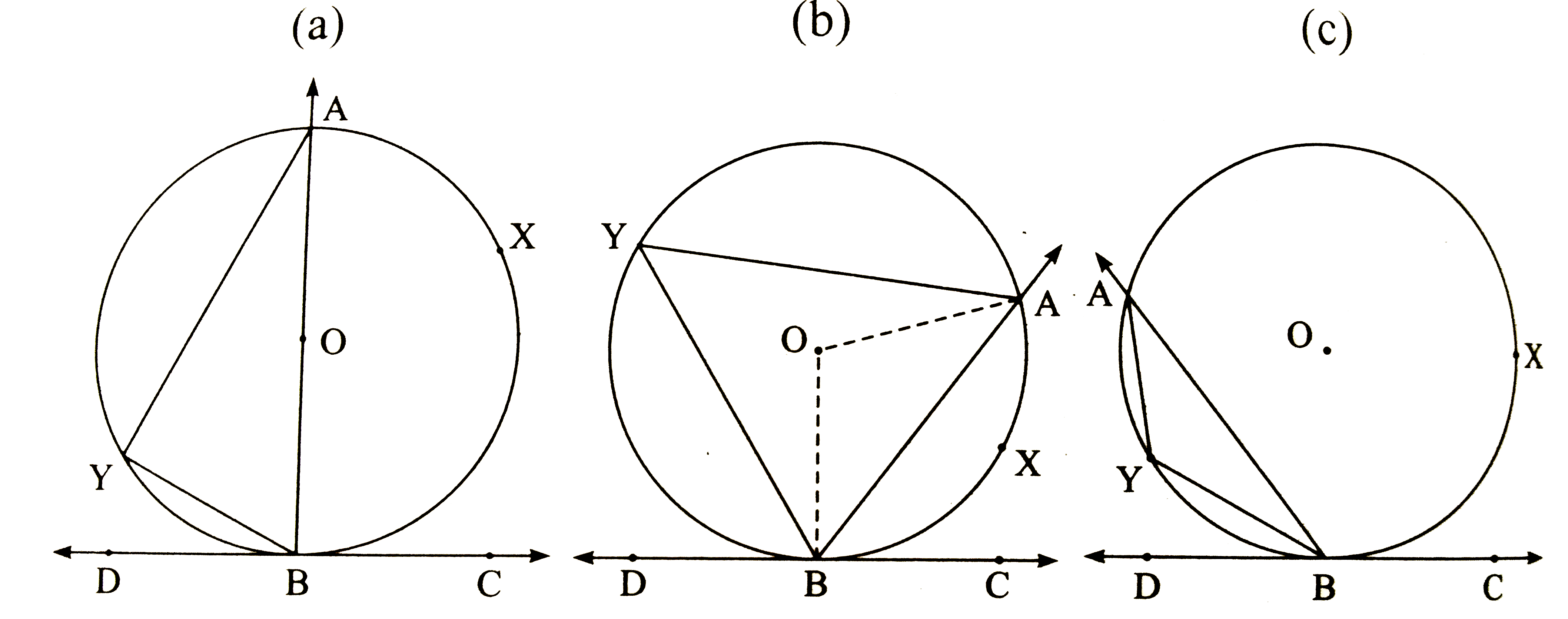
Given : Let O be the centre of the circle. Line DBC is tangent to the circle at point B. Seg BA is a chord of the circle. Point X of the circle is on C side of line BA and point Y of the circle is on D side of line BA.
To prove : m ∠ABC=12m(arcAXB).
View SolutionTheorem 2 : The no. of Radians in an angle subtended by an arc of a circle at the centre = arc/radius
View SolutionFind tge degree measure of the angle subtended at the centre of a circle of diameter 60 cm by an arc of length 16.5 cm.
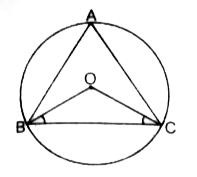
View SolutionBC is a chord to a circle with centre O. A is a point on major are BC as shown in the below figure. What is the value of ∠BAC+∠OBC ?
View SolutionIn the figure , in a circle with centre O, length of chord AB is equal to the radius of the circle. Find the measure of each of the following :
(1) ∠AOB
(2) ∠ACB
(3) arc AB
(4) arc ACB

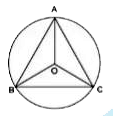
View SolutionIf the angle subtended at the center the circle by arc BC is 100∘. Then calculate the value of ∠BAC.
View Solution
