It is known that 60% of mice inoculated with a serum are protected from a certain disease. If 5 mice are inoculated, find the probability that (a) None contract the disease (b) More than 3 contract the disease.
Let X be the number of mice that contract the disease.
Then, X follows a binomial distribution with {n}=5.
Let p be the probability of mice that contract the disease.
∴p=0.4andq=0.6
Hence, the distribution is given by
P(X=r)=5Cr(0.4)r(0.6)5−r,r=0,1,2,3,4,5
P(X>3)=P(X=4)+P(X=5)
=5C4(0.4)4(0.6)5−4+5C5(0.4)5(0.6)5−5
=0.0768+0.01024
=0.08704
Topper's Solved these Questions
Similar Questions
It is known that 60% of mice inoculated with a serum are protected from a certain disease. If 5 mice are inoculated, find the probability that (a) None contract the disease (b) More than 3 contract the disease.
View SolutionA laboratory blood test is 99% effective in detecting a certain disease when it is in fact, present. However, the test also yields a false positive result for 0.5% of the healthy person tested (i.e. if a healthy person is tested, then, with probability 0.005, the test will imply he has the disease). If 0.1 percent of the population actually has the disease, what is the probability that a person has the disease given that his test result is positive?
View Solution
Knowledge Check
- Question 1 - Select One
The records of a hospital show that 10% of the cases of a certain disease are fatal. If 6 patients are suffering from the disease, then the probability that only three will die is
A1458×10−5B1458×10−6C41×10−6D8748×10−5 - Question 2 - Select One
The records of a hospital show that 10% of the cases of a certain disease are fatal. If 6 patients are suffering from the disease, then the probability that only three will die, is
A1458×10−5B1458×10−6C41×10−6D8748×10−5 - Question 3 - Select One
The records of a hospital show that 10% of the cases of a certain disease are fatal. If 6 patients are suffering from the disease, then the probability that only three will die, is
A1458×10−5B1458×10−6C41×10−6D8748×10−5
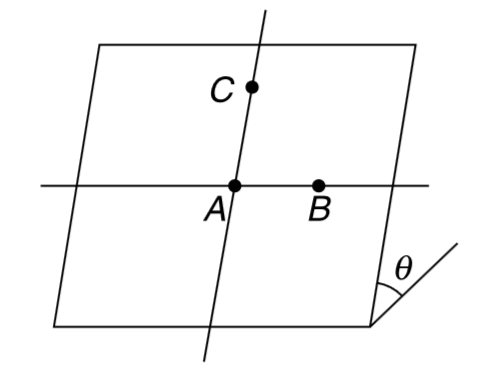
It is known that there exists a uniform electric field in a certain region. Imagine an incline plane (figure) in the region which is inclined at θ=37∘ to the horizontal when one moves horizontally along the incline from A to B (AB=1cm), the electric potential decreases by 10V. Similarly, potential at C(AC=1cm) is less than potential at A by 10 V where line AC lies on the incline and is perpendicualr to AB. When one moves vertically up from point A to a point D(AD=1cm), the potential drop by 10 V again. Find the magnitude of the electric field in the region and the angle that it makes with vertical [given sin37∘=35]
 View Solution
View SolutionFive mice in a stable population of 500 are intentionally infected with a contagious disease to test a theory of epidemic spred that postulates the rate of change in the infected population is proportional to the product of the number of mice who have the disease with the number that are disease free. Assuming the theory is correct, how long will it take half the popullation to contract the disease?
View SolutionIf the records of a hospital show that 10% of the cases of a certain disease are fatal if 6 patients are suffering from the disease then the probability that only three will die is
View SolutionFrom a group of 5 boys and 3 girls, three persons are chosen at random. Find the probability that there are more girls than boys
View SolutionOne percent of the population suffers from a certain disease. There is blood test for this disease, and it is 99% accurate, in other words, the probability that it gives the correct anwer is 0.99, regardless of whether the person is sick or healthy. A person takes the blood test, and the result says that he has the disease. The probability that he actualy has the disease is
View Solution

