l, m and n are three parallel lines intersected by transversals p and q such that l, mand n cut off equal intercepts AB and BC on p (see Fig. 8.28). Show that l, m and n cut off equal intercepts DE and EF on q also
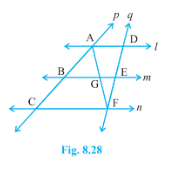
Given:
and cut off equal intercepts and on p
So,
To prove:l,m and n cut off equal intercepts DE and EF on q
i.e.,
Proof:In ,
B is the mid-point of AC as and since
So,G is the mid-point of AF using line drawn throught mid-point of one side of a triangle, parallel to another side, bisects the third side.
In ,
G is the mid-point of AF
and
since
So,E is the mid-point of DF using line drawn throught mid-point of one side of a triangle, parallel to another side, bisects the third side.
Since E is the mid-point of DF
Hence proved.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Two parallel line l and m are intersected by a transversal p. The quadrilateral formed by the bisectors of interior angles is a
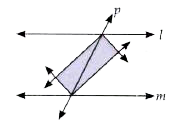 ATrapeziumBKiteCParallelogramDSquare
ATrapeziumBKiteCParallelogramDSquare
l and m are two parallel lines intersected by another pair of parallel lines p and q. Show that △ABC≅△CDA.
View SolutionIn Fig. 5.60, two parallel lines l and m are cut by two transversals n and p. Find the values of x and y.
 View Solution
View SolutionIn Fig.5.66 , two parallel lines l and m are cut by two transversals p and q . Determine the values of x and y .
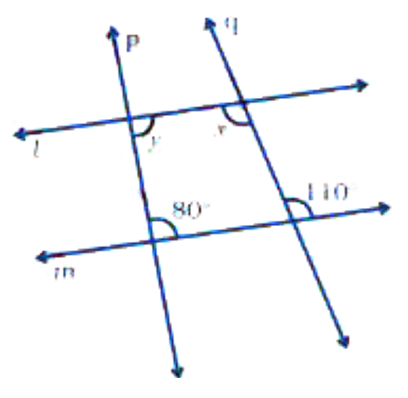 View Solution
View Solutionl and m are two parallel lines intersected by another pair of parallel lines p and q (see Fig. 7.19). Show that ΔABC≅ΔCDA.
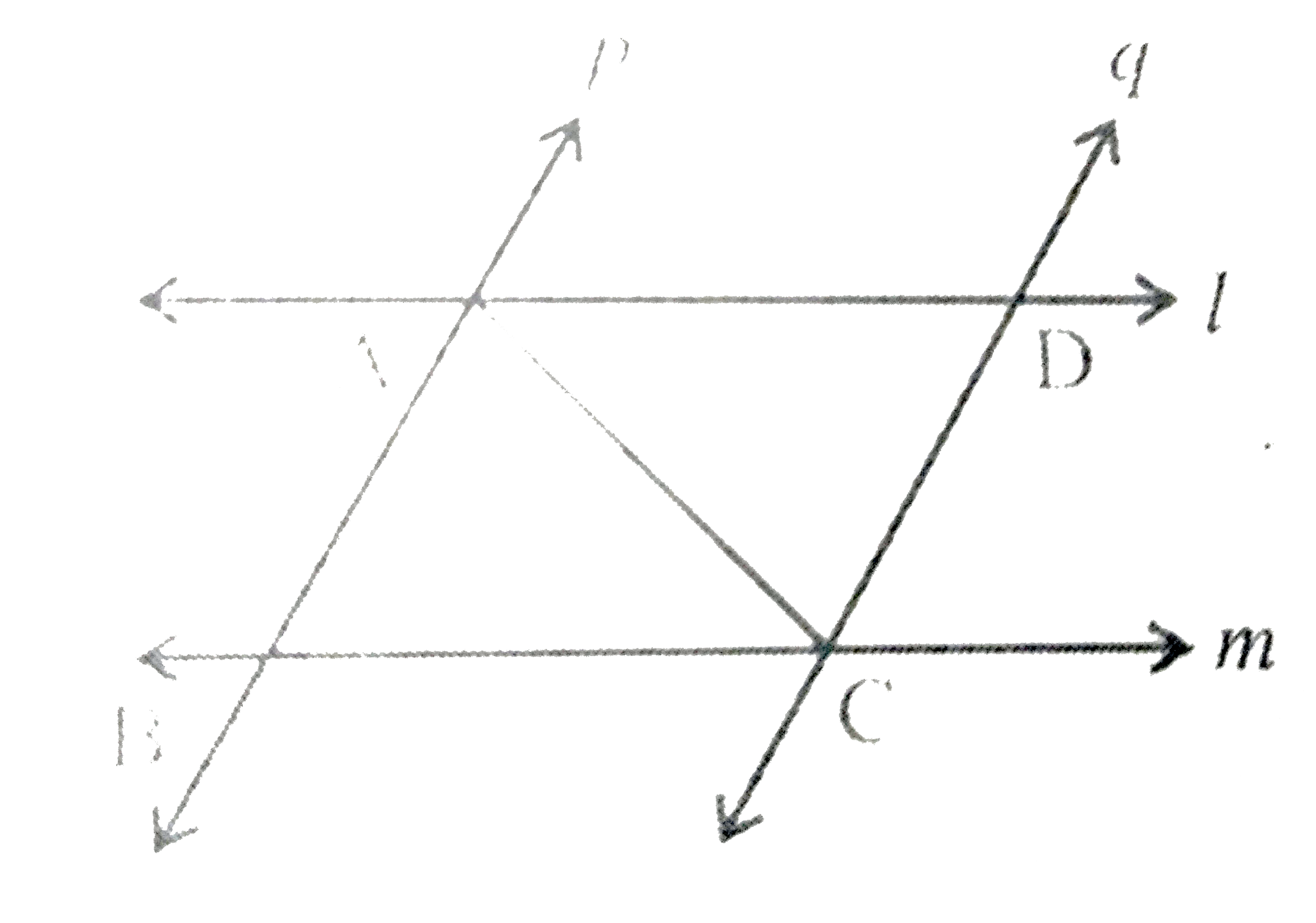 View Solution
View Solutionl and m are two parallel lines intersected by another pair of parallel lines p and q as shown in figure. Show that ABC≅CDA.
 View Solution
View SolutionIn Fig. 60, AB and CD are parallel lines intersected by a transversal PQ at L and M respectively. If ∠LMD=350 find ∠PLA.
View SolutionIn thg given figure, two parallel lines l and m are intersected by two parallel lines p and q.
Show that ΔABC≅ΔCDA.
 View Solution
View Solution