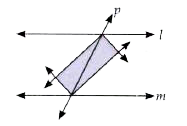
Two parallel lines l and m are intersected by a transversal p (see Fig. 8.15). Show that the quadrilateral formed by the bisectors of interior angles is a rectangle.
∴∠PAC=∠ACR=2Q
∴∠BAC=∠PAB=Q
∴∠BAc=∠ACD=Q
AB||CD⟨'∠BAC=∠ACD)
CB||AD
∠PAC+∠SAC=1800
12(PAC)+12(SAS)=900
∠ABC+∠CAB=900
Similar Questions
Knowledge Check
- Question 1 - Select One
Two parallel line l and m are intersected by a transversal p. The quadrilateral formed by the bisectors of interior angles is a
 ATrapeziumBKiteCParallelogramDSquare
ATrapeziumBKiteCParallelogramDSquare - Question 2 - Select One
Two parallel lines AB and CD are intersected by a transversal EF at M and N respectively.
The lines MP and NP are the bisectors of interior angles ∠BMN and ∠DNM on the same side of the transversal. Then ∠MPN is equal to :A60∘B90∘C45∘D120∘ - Question 3 - Select One
Two parallel lines AB and CD are intersected by a transversal EF at M and N respectively.
The lines MP and NP are the bisectors of interior angles ∠BMN and ∠DNM on the same side of the transversal. Then ∠MPN is equal to :A60∘B90∘C45∘D120∘
If two parallel lines are intersected by a transversal, prove that the bisectors of the two pairs of interior angles enclose a rectangle.
View SolutionIf two parallel lines intersected by a transversal; prove that the bisectors of the two pairs of interior angle encloses a rectangle.
View SolutionTwo parallel lines AB and CD are intersected by a transversal line EF at M and N, respectively. If the lines MP and NP are the bisectors of the interior angles BMN and DNM on the same side of the transversal, then ∠MPN is equal to
View SolutionTwo parallel lines AB and CD are intersected by a transversal line EF at M and N, respectively. If the lines MP and NP are the bisectors of the interior angles BMN and DNM on the same side of the transversal, then ∠MPN is equal to
View SolutionIf two parallel lines are intersected by a transversal , then the interior angles on the same side of the transversal are -
View Solution

