Let 2x2+y2−3xy=0 be the equation of pair of tangents drawn from the origin to a circle of radius 3, with center in the first quadrant. If A is the point of contact. Find OA
The correct Answer is:3(3+√10)
The equation o2x2−3xy+y2=0 represents a pair of tangents OA and OA'.
Let the angle between these two tangents be 2θ. Then,
tan2θ=2√(−3/2)2−2×12+1
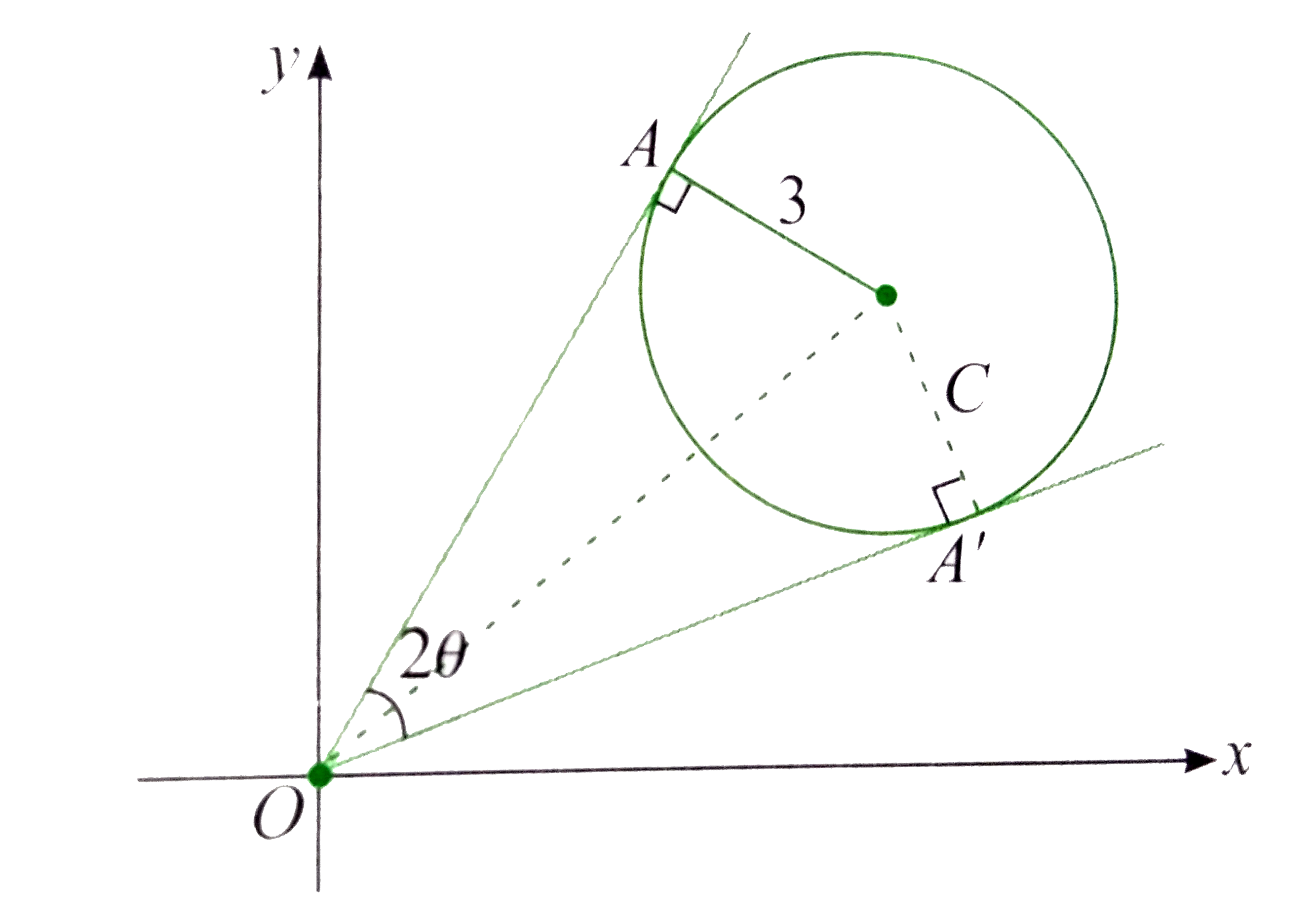
or 2tanθ1−tan2θ=13
or tan2θ+6tanθ−1=0
or tanθ=−6±√36+42=−3±√10
Now, we know that the line joining the point through which tangents are drawn to the center bisects the angle between the tangents. Therefore,
∠AOC=θ
In ΔOAC,
tanθ=3OA
or OA=3√10−3×√10+3√10+3
∴OA=3(3+√10)
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.5
12 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.6
5 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.3
18 Videos
- BINOMIAL THEORMBOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank
31 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
Similar Questions
Let 2x2+y2−3xy=0 be the equation of pair of tangents drawn from the origin to a circle of radius 3, with center in the first quadrant. If A is the point of contact. Find OA
View SolutionLet 2x2+y2−3xy=0 be the equation of a pair of tangents drawn from the origin O to a circle of radius 3 with centre in the first quadrant. If A is one of the points of contact, then the length of OA is
View Solution
Knowledge Check
The equation of tangents drawn from the origin to the circle x2+y2−2rx−2hy+h2=0 are :
Ax=0By=0C(h2−r2)x−2rhy=0D(h2−r2)x+2hy=0The equation of tangents drawn from the origin to the circle x2+y2−2rx−2hy+h2=0 are
Ax=0By=0C(h2−r2)x−2rhy=0D(h2−r2)x+2rhy=0The equation of tangents drawn from the origin to the circle x2+y2−2rx−2hy+h2=0 are
Ax=0By=0C(h2−r2)x−2rhy=0D(h2−r2)x+2hy=0
The equation of pair of tangents drawn from the point (0,1) to the circle x2+y2–2x+4y=0 is–
View SolutionCombined equation to the pair of tangents drawn from the origin to circle x2+y2+4x+6y+9=0 is
View SolutionThe equation of tangents drawn from the origin to the circlex2+y2−2rx−2hy+h2=0
View SolutionCombined equation to the pair of tangents drawn from the origin to the circle x2+y2+4x+6y+9=0 is
View SolutionThe equation of tangents drawn from the point (0,1) to the circle x2+y2−4x−2y+4=0 are
View Solution
