Let ABC be a triangle with AB=AC. If D is the midpoint of BC,E is the foot of the perpendicular drawn from D to AC,andF is the midpoint of DE, then prove that AF is perpendicular to BE.
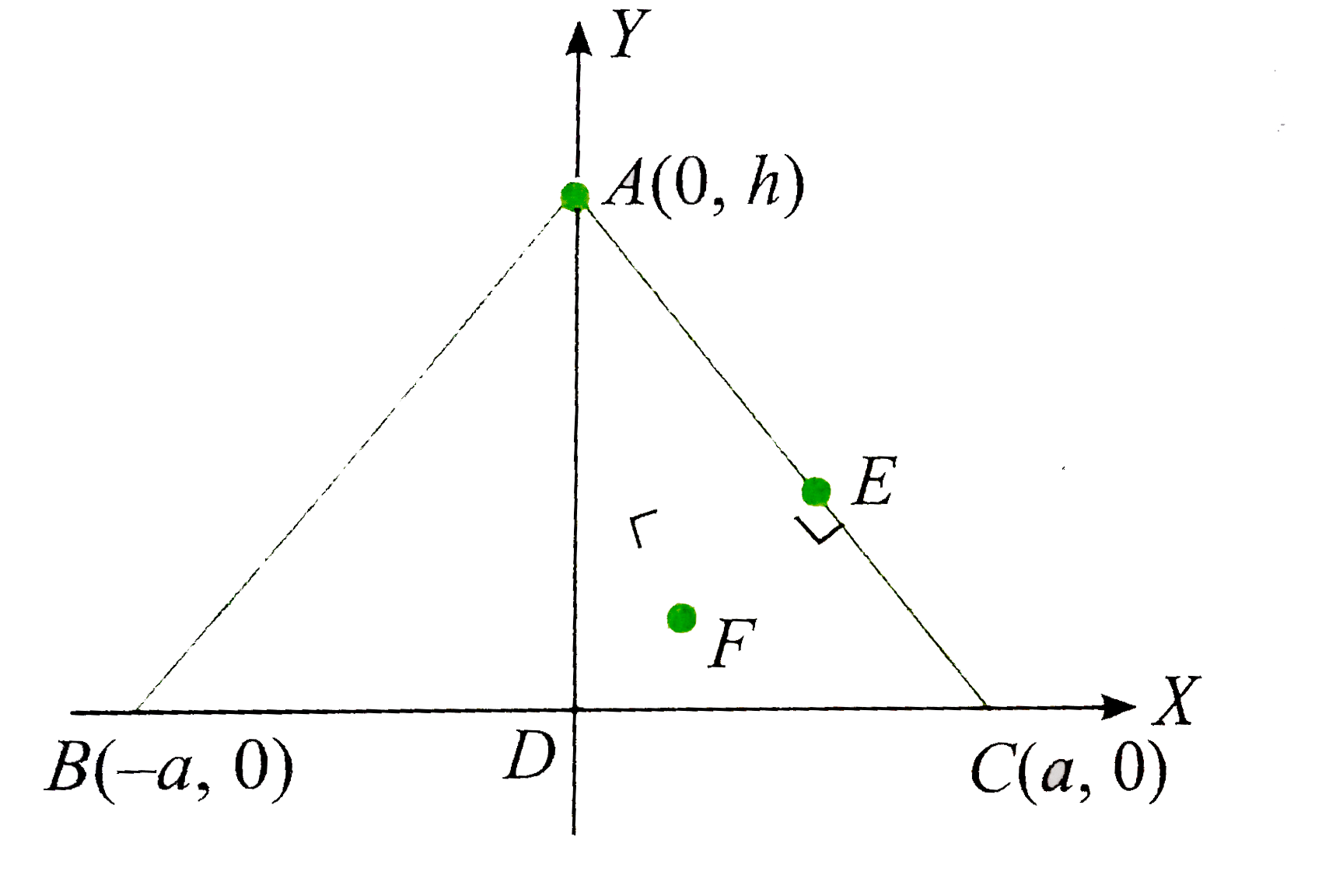
Let BC be taken as the x-axis with the origin at D. Let A be taken on y-axis. Let BC=2a. Now AB=AC, then the coordinates of B and C are (-a,0) and (a,0), respectively. Let DA =h. Then the coordiantes of A are (0,h).
Hene, the equation of AC is ltbgt xa+yh=1 (1)
and the equation of DE perpendicular to AC and passing through the origin is
xh−ya=0
or x=hya (2)
Solving (1) and (2), we get the coordinates of E as follows:
hya2+yh=1
or h2y+a2y=a2h
or y=a2ha2+h2
∴x=aha2+h2
∴E≡(ah2a2+h2,a2ha2+h2)
Since F is the midpoint of DE, its coordinates are
(ah22(a2+h2),a2h2(a2+h2))
The slope of AF is
m1=h−a2h2(a2+h2)0−ah22(a2+h2)
2h(a2+h2)−a2h−ah2=a2+2h2ah (1)
and the slope of BE is
m2=a2ha2+h2−0ah2a2+h2+a
=a2hah2+a3+ah2=aha2+2h2 (2)
From (1) and (2), we have
m1m2=−1
or AF⊥BE
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.123videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.24videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)1videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
ABC is a triangle and D is the mid-point of BC . The perpendiculars from D to AB and AC are equal. Prove that the triangle is isosceles.
View SolutionABC is a triangle and D is the mid-point of BC . The perpendiculars from D to AB and AC are equal. Prove that the triangle is isosceles.
View SolutionABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that area of BED=14areaofABC.
View SolutionIn Figure, if AB∣∣DC and P is the mid-point BD, prove that P is also the midpoint of AC
View SolutionIn Figure, ABC is a right triangle right angled at B and D is the foot of the the perpendicular drawn from B on AC . If DM⊥BC and DN⊥AB , prove that: (i)DM2=DN×MC (ii)DN2=DM×AN
View SolutionLet ABC be an isosceles triangle with AB=AC and let D, E, F be the mid points of BC, CA and AB respectively. Show that AD⊥FE and AD is bisected by FE.
View SolutionIn Figure, AD is a median and BL, CM are perpendiculars drawn from B and C respectively on AD and AD produced. Prove that BL=CM
View SolutionIf ABC is an isosceles triangle with AB=AC. Prove that the perpendiculars from the vertices B and C to their opposite sides are equal.
View SolutionOABC is regular tetrahedron in which D is the circumcentre of OAB and E is the midpoint of edge AC. Prove that DE is equal to half the edge of tetrahedron.
View SolutionOABC is regular tetrahedron in which D is the circumcentre of OAB and E is the midpoint of edge AC. Prove that DE is equal to half the edge of tetrahedron.
View Solution

