Question

Let a circle be given by $2x(x-1)+y(2y-b)=0,(a\ne 0,b\ne 0)$
. Find the condition on $aandb$
if two chords each bisected by the x-axis, can be drawn to the circle
from $(a,\frac{b}{2})$

Explanation

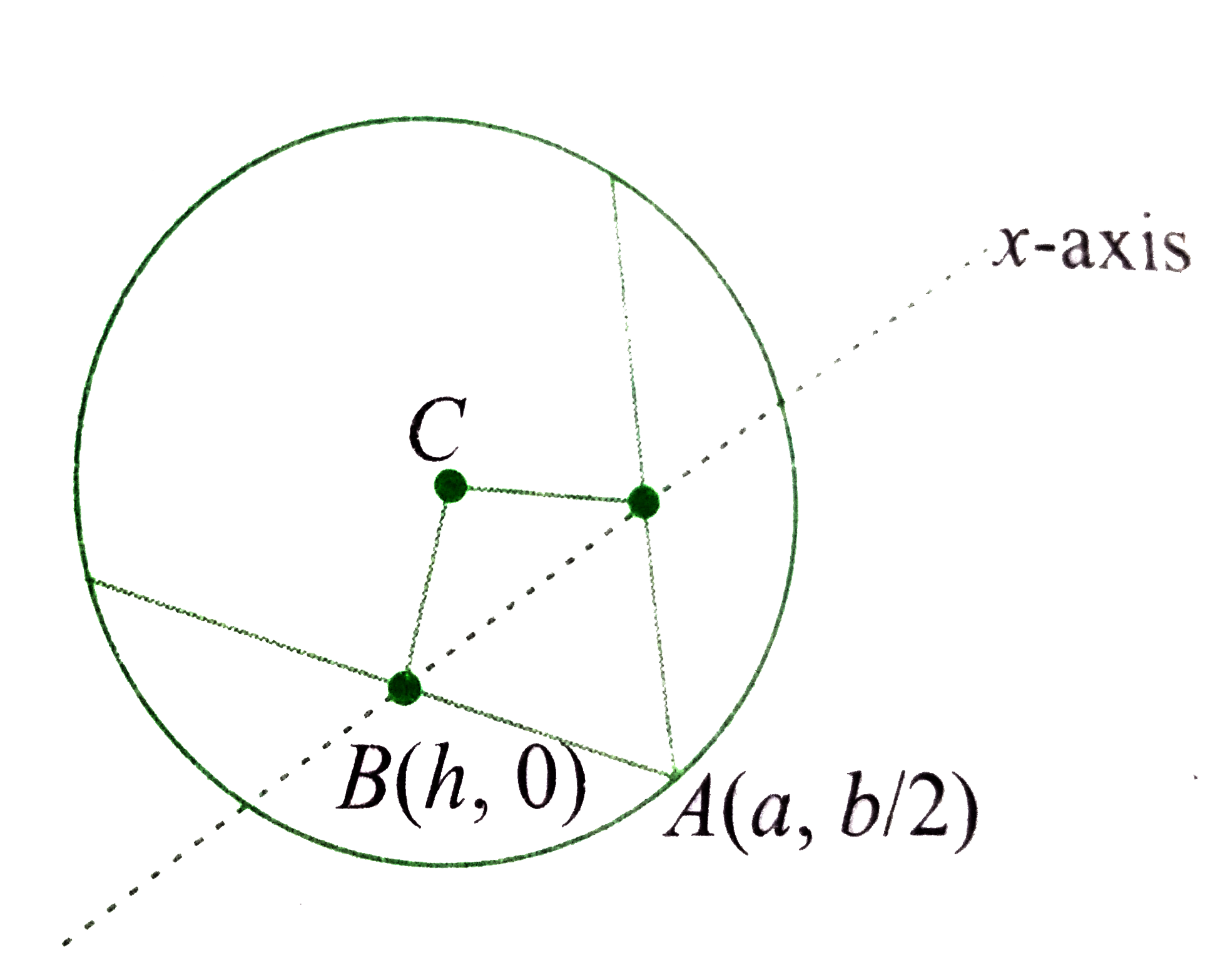
The given circle is
`2x(x-a)+y(2y-b)=0(a,b cancel(=)0)`
or `x^(2)+y^(2)-ax-(b)/(2)y=0`
Its center is `C(a//2,b//4)`.
Also, point `A(a,b//2)` lies on the circle.
Since chord is bisected at point B (h,0) on the x-axis, we have
(Slope of BC) `xx` (Slope of AB ) `= -1`
or `{((b//s)-0)/((a//2)-h)}{((b//2)-0)/(a-h)}=-1`
`h^(2)-3 (a)/(2)h+(a^(2))/(2)+(b^(2))/(8)=0`

Since two such chords exist, the above equation must have tow distinct real roots, for which its discrimination must be positive i.e.,
or `(9a^(2))/(4)-4((a^(2))/(2)+(b^(2))/(8))gt0`
or `a^(2) gt 2b^(2)`