Let a sample space be S={ω1,ω2,....,ω6}. Which of the following assignments of probabilities to each outcome are valid?

(a) Condition (i): Each of the number p(omega_i) is positive and less than one.
Condition (ii): Sum of probabilities
=16+16+16+16+16+16+16=1Therefore, the assignment is valid
(b) Condition (i): Each of the number p(ωi) is either 0 or 1.
Condition (ii) Sum of the probabilities =1+0+0+0+0+0=1
Therefore, the assignment is valid
(c) Condition (i) Two of the probabilities p(ω5)andp(ω6) are negative, the assignment is not valid
(d) Since p(ω6)=32>1, the assignment is not valid
(e) Since, sum of probabilities =0.1+0.2+0.3+0.4+0.5+0.6=2.1, the assignment is not valid.
Topper's Solved these Questions
- PROBABILITYBOOK - NCERTCHAPTER - PROBABILITYEXERCISE - MISCELLANEOUS EXERCISE
10 Videos
- PROBABILITYBOOK - NCERTCHAPTER - PROBABILITYEXERCISE - EXERCISE 16.1
16 Videos
- PROBABILITYBOOK - NCERTCHAPTER - PROBABILITYEXERCISE - EXERCISE 16.3
21 Videos
- PRINCIPLE OF MATHEMATICAL INDUCTIONBOOK - NCERTCHAPTER - PRINCIPLE OF MATHEMATICAL INDUCTIONEXERCISE - EXERCISE 4.1
24 Videos
- RELATIONS AND FUNCTIONSBOOK - NCERTCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 2.3
5 Videos
Similar Questions
Let a sample space be:
S={ω1,ω2,…..ωn}. Which of the following assignments of probability to each outcome are valid?
Outcomes ω1,ω2,ω3,ω4,ω5,ω6
a. 16,16,16,16,16,16
b. 1,0,0,0,0,0
c. 18,23,13,13,−14,−13
d. 112,112,16,16,16,32
e. 0.1,0.2,0.3,0.4,0.5,0.6
View SolutionWhich of the following cannot be valid assignment of probabilities for outcomes of sample Space S={ω1,ω2,ω3,ω4,ω5,ω6,ω7}
View Solution
Knowledge Check
Consider two complex number z and ω satisfying |z|=1 and |ω−2|+|ω−4|=2. Then which of the following statements(s) is (are) correct?
ARe(zω) can never exceed 4BIf argz=argω,then |z+2|is equal to 3CThe minimum value of |z−ω| to equal to 2DThe maximum value of |z−ω| is equal to 6If 1,ω,ω2,…..,ωn−1 are the nth roots of unity, then (2−ω)(2−ω2)….(2−ωn−1) equals
A2n−1BnC1+nC2+….+nCnC[^(2n+1)C0+2n+1C1+….+2n+1Cn]1/2−1DNone of these
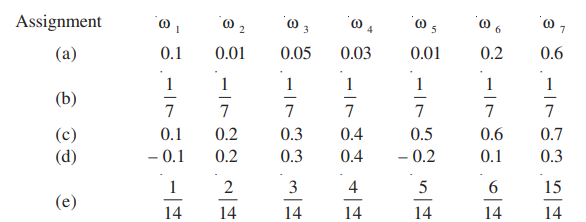
Which of the following cannot be valid assignmentof probabilities for outcomes of sample space
S={ω1,ω2,ω3,ω4,ω5,ω6,ω7}?
Assignement ω1,ω2,ω3,ω4,ω5,ω6,ω7
a. 0.1,0.01,0.05,0.03,0.01,0.3,0.6
b. 17,17,17,17,17,17,17
c. 0.1,0.2,0.3,0.4,0.5,0.6,0.7
d. -0.1,0.2,0.3,0.4,-0.2,0.1,0.3
e. 114,214,314,414,514,614,1514
View SolutionWhich of the following cannot be valid assignment of probabilities for outcomes of sample space S={W1,W2,W3,W4,W5,W6,W7}
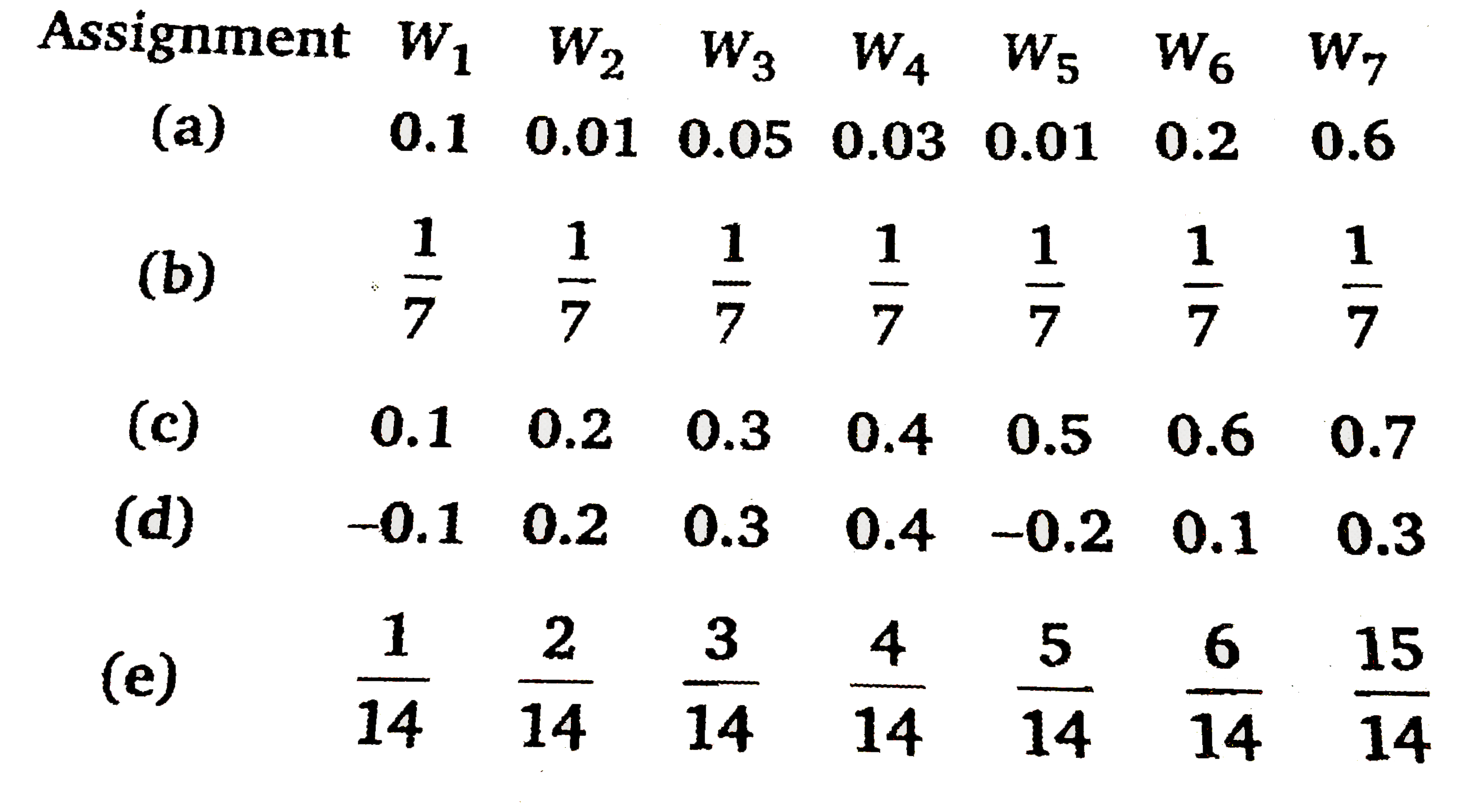
View SolutionCompare the power used in the 2 ω resistor in each of the following circuits :
a 6 V battery in series with 1 ω and 2 ω resistors, and
View Solution∣∣ ∣ ∣∣1ωω2ωω21ω21ω∣∣ ∣ ∣∣
View Solution∣∣ ∣ ∣∣1ωω2ωω21ω21ω∣∣ ∣ ∣∣=
View SolutionLet ω1 and ω2 be the roots of ω2+aω+b=0. If origin, ω1 and ω2 form an equilateral triangle then
View Solution
