Let a sample space be:
S={ω1,ω2,…..ωn}. Which of the following assignments of probability to each outcome are valid?
Outcomes ω1,ω2,ω3,ω4,ω5,ω6
a. 16,16,16,16,16,16
b. 1,0,0,0,0,0
c. 18,23,13,13,−14,−13
d. 112,112,16,16,16,32
e. 0.1,0.2,0.3,0.4,0.5,0.6
The correct Answer is:not valid
Step by step video, text & image solution for Let a sample space be: S={omega_(1),omega_(2),…..omega_(n)}. Which of the following assignments of probability to each outcome are valid? Outcomes omega_(1),omega_(2),omega_(3),omega_(4), omega_(5),omega_(6) a. 1/6,1/6,1/6,1/6,1/6,1/6 b. 1,0,0,0,0,0 c. 1/8,2/3,1/3,1/3,-1/4,-1/3 d. 1/12,1/12,1/6,1/6,1/6,3/2 e. 0.1,0.2,0.3,0.4,0.5,0.6 by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - EXERCISE 16 (a) SHORT ANSWER TYPE QUESTIONSSATQ11videos
PROBABILITY
- BOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - EXERCISE 16 (B) SHORT ANSWER TYPE QUESTIONSSATQ10videos
PROBABILITY
- BOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - CHAPTER TEST12videos
PROBABILITY
- BOOK - MODERN PUBLICATIONCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - CHAPTER TEST12videos
PERMUTATIONS AND COMBINATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Chapter Test11videos
RELATIONS AND FUNCTIONS
Similar Questions
Let a sample space be S={ω1,ω2,....,ω6}. Which of the following assignments of probabilities to each outcome are valid?
 View Solution
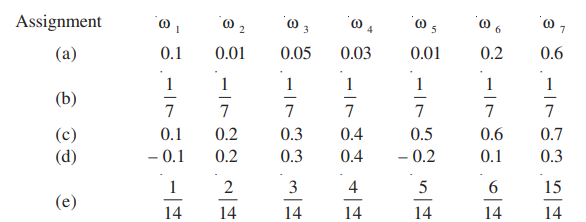
View SolutionWhich of the following cannot be valid assignmentof probabilities for outcomes of sample space
S={ω1,ω2,ω3,ω4,ω5,ω6,ω7}?
Assignement ω1,ω2,ω3,ω4,ω5,ω6,ω7
a. 0.1,0.01,0.05,0.03,0.01,0.3,0.6
b. 17,17,17,17,17,17,17
c. 0.1,0.2,0.3,0.4,0.5,0.6,0.7
d. -0.1,0.2,0.3,0.4,-0.2,0.1,0.3
e. 114,214,314,414,514,614,1514View Solution
Knowledge Check
- Question 1 - Select One
Given that ⎡⎢⎣1ωω2ωω21ω21ω⎤⎥⎦⎡⎢⎣k11111111⎤⎥⎦=⎡⎢⎣000000000⎤⎥⎦ then k=
A6B1C8D9 - Question 2 - Select One
If ω is a complex cube root of unity, then (1−ω+ω2)6+(1−ω2+ω)6=
A0B6C64D128
11+2ω+12+ω−11+ω=0
View SolutionIf ω is the cube root of unity then find the value of ∣∣ ∣ ∣∣1ω6ω8ω6ω3ω7ω8ω71∣∣ ∣ ∣∣
View SolutionWhich of the following cannot be valid assignment of probabilities for outcomes of sample Space S={ω1,ω2,ω3,ω4,ω5,ω6,ω7}
 View Solution
View SolutionIf ω is an imaginary cube root of unity, then find the value of (1+ω)(1+ω2)(1+ω3)(1+ω4)(1+ω5)........(1+ω3n)=
View SolutionIf 1,x1,x2,x3 are the roots of x4−1=0andω is a complex cube root of unity, find the value of (ω2−x1)(ω2−x2)(ω2−x3)(ω−x1)(ω−x2)(ω−x3)
View SolutionIf ω is a cube root of unity, prove that
(1+ω−ω2)3−(1−ω+ω2)3=0View Solution

