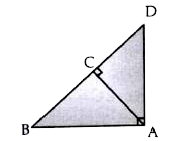
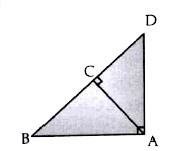
Let ABC be a triangle, right-angled at B and D be the midpoint of AC. Show that DA = DB = DC.
Video Solution
Text Solution

Through D, draw DE||BC, meeting AB at E.
Now, ∠AED=∠ABC=90∘ [corres. ∠]
∴∠BED=∠AED=90∘[∵∠AED+∠BED=180∘].
Now, in △ABC, it is given that D is the midpoint of AC and DE||BC (by construction).
∴ E must be the midpoint of AB (by converse of midpoint theorem).
∴AE=BE.
Now, in △ AED and BED, we have
AE=BE (proved), ED=ED (common),
∠AED=∠BED (each equal to 90∘).
∴△AED≅△BED
∴DA=DB.
But, DA=DC [∵ D is the midpoint of AC].
Hence, DA=DB=DC.
|
Topper's Solved these Questions
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - EXAMPLE
32 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Exercise 10 A
10 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
Similar Questions
Knowledge Check
Let ABC be an acute-angled triangle and let D be the midpoint of BC. If AB = AD, then tan(B)/tan(C) equals
A√2B√3C2D3ABC is right angled triangle, right angled at C . D is the midpoint of BC. Then , tanθtanϕ =
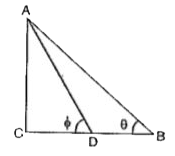 A1B1√2C12D2
A1B1√2C12D2
In a triangle ABC, right angled at B, then
View SolutionIn the figure given below ABC is a triangle right angled at A and AC ⊥ BD . Show that

AB2=BC×BD
View SolutionIn the given figure ABC is a right angled triangle with ∠B=90∘ . D is the mid -point of BC . Show that AC2=AD2+3CD2 .
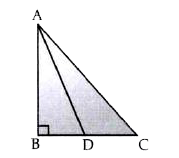
View SolutionABC is a right triangle with right angle at B , if P is a mid point of AC show that PB=PA=PC=12(AC)
View SolutionABC is a triangle right-angled at B and D is a point on BC produced (BD > BC), such that BD = 2 DC. Which one of the following is correct?
View SolutionABC is a triangle right angled at B. D is a point on AC such that ∠ABD=45∘ If AC=6 and AD=2 then AB=
View Solution