Let ABCD be a traezium with AD parallel to BC. Assume there is a point M in the interior of the segement BC such that AB=AM and DC=DM . Then the ratio of the area of the tapezium to the area of triabgle AMD is -

A

2

B

3

C

4

D

Not determinable from data

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

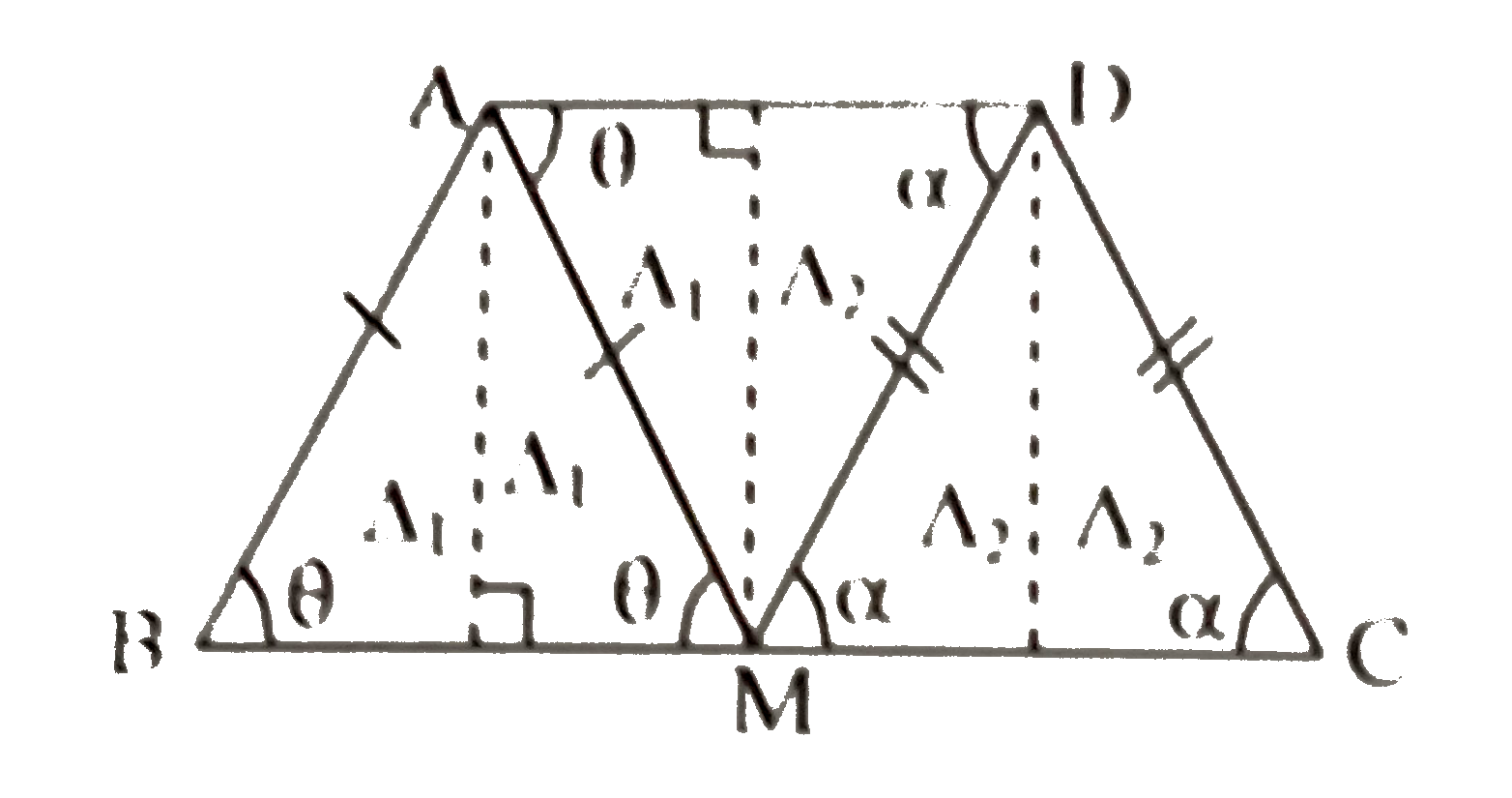
$\frac{ar(ABCD)}{ar(AMD)} = \frac{3_{Δ} + 3_{Δ 2}}{Δ_{1} + Δ_{2}} = \frac{3}{1}$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Similar Questions

ABCD is a parallelogram. E is a point on BC such that BE : EC = m:n. If AE and DB intersect in F, then what is the ratio of the area of triangle FEB to the area of triangle AFD?
View Solution
In the adjoining figure, $D E$ is parallel to $B C$ and $A D = 1 c m$ , $B D = 2 c m$ . What is the ratio of the area of $A B C$ to the area of $A D E$ ?
View Solution

Knowledge Check

Question 1 - Select One
ABCD is a trapezium in which $A B ∣ ∣ C D$ and $A B = 2 C D$ . It its diagonals intersect each other at O then ratio of the area of triangle AOB and COD is
A $1 : 2$
B $2 : 1$
C $4 : 1$
D $1 : 4$
Question 2 - Select One
In a trapezium ABCD, AB is a parallel to CD. BD is perpendicular to AD. AC is perpendicular to BC. If $A D = B C = 15 c m and A B = 25 c m$ , then the area of the trapezium is :
A $192 c m^{2}$
B $232 c m^{2}$
C $172 c m^{2}$
Dnone of these
Question 3 - Select One
Let ABCD be a trapezium in which AB||DC and E be the mid-point of AD. If F be a point on BC such that EF||AB. Then EF, where F is the mid-point of BC, is equal to

AAB + DC
B $\frac{1}{2} (A B + D C)$
C $\frac{1}{3} (A B + D C)$
DNone of these

Recommended Questions

Home
Ask Doubt
Profile