Let ABCDEFGHIJKL be a regular dodecagon. Then the value of is equal to ____Solution in Bengali
The correct Answer is:4
Similarly,

Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Single correct Answer type)2videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (JEE Advanced)3videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Matrix match type6videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE )8videos
PROGRESSION AND SERIES
- BOOK - CENGAGE PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - All Questions1119videos
RELATIONS AND FUNCTIONS
Similar Questions
For a regular polygon, let r and R be the radii of the inscribed and the circumscribed circles. A false statement among the following is
03:26View SolutionLet ABC be a triangle such that ∠ACB=π6 and let a , b and c denote the lengths of the side opposite to A,B ,and C respectively. The value(s) of x for which a=x2+x+1,b=x2−1,and c=2x+1 is(are) −(2+√3) (b) 1+√3 (c)2+√3 (d) 4√3
02:40View Solutionshow that tan−1(12)+tan−1(211)=tan−1(34)
View SolutionLet Sk,k=1,2,….100 denote the sum of the infinite geometric series whose first term is k−1K! and the common
ration is 1k then the value of (100)2100!+Σ100k=1|(k^2-3k+1)S_k| is ____________03:19View SolutionIf the function f:[1,∞)→[1,∞) is defined by f(x)=2x(x−1), then find f−1(x)
05:54View SolutionIf ABCDEF is a regular hexagon inscribed in a ( circle with centre O, then the value of )/(AB)+bar(AC)+bar(AD)+( then the value of )/(AF) equals
03:11View SolutionIn a regular hexagon ABCDEF, prove that −−→AB+−−→AC+−−→AD+−−→AE+−−→AF=3−−→AD
04:32View SolutionLet ABCDEFGHIJKL be a regular dodecagon. Then the value of ABAF+AFAB is equal to ____
02:34View SolutionIf ABCDEF is a regular hexagon , then
¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF =03:43View SolutionIf ABCDEF is a regular hexagon, then ¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF=
01:48View SolutionIf ABCDEF is a regular hexagon and AB+AC+AD+AE+AF=λAD then λ is equal to
02:53View SolutionIf ABCDEF is a regular hexagon of side a, then ¯¯¯¯¯¯AB.¯¯¯¯¯¯AF=
05:17View SolutionIn the given figure, AB|| CD. Find the value af x.
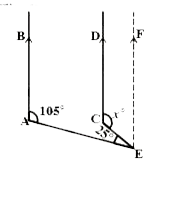 06:20View Solution
06:20View SolutionIn the given figure, AB|| CD. Find the value af x.
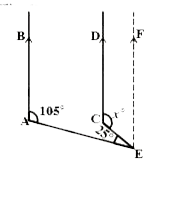 03:03View Solution
03:03View SolutionIn the given figure, AB|| CD. Find the value af x.
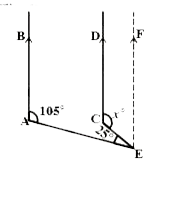 07:54View Solution
07:54View SolutionIn the given figure, AB|| CD. Find the value af x.
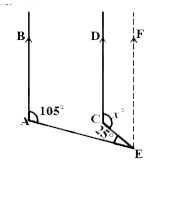 04:19View Solution
04:19View Solution

