Let 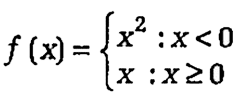.Area bounded by the curve $y = f (x), y = 0 and x^{2} = 9 a^{2} i s 9 \frac{a}{2}$ Then $a =$ …..............

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $1 / 2$

Answer

Step by step video, text & image solution for Let .Area bounded by the curve y=f(x),y=0 and x^(2)=9a^(2) is 9a/2 Then a= ….............. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

AREA OF CURVESBOOK - ML KHANNACHAPTER - AREA OF CURVESEXERCISE - SELF ASSESSEMENT TEST
16 Videos
AREA OF CURVESBOOK - ML KHANNACHAPTER - AREA OF CURVESEXERCISE - PROBLEM SET (1) (TRUE AND FALSE)
9 Videos
ADDITION AND MULTIPLICATION OF VECTORS BOOK - ML KHANNACHAPTER - ADDITION AND MULTIPLICATION OF VECTORS EXERCISE - Self Assessment Test (Comprehension)
3 Videos
BINOMIAL THEOREM AND MATHEMATICAL INDUCTION BOOK - ML KHANNACHAPTER - BINOMIAL THEOREM AND MATHEMATICAL INDUCTION EXERCISE - Self Assessment Test
35 Videos

Knowledge Check

The area bounded by the curves $y^{2} - x = 0$ and $y - x^{2} = 0$ is
A $\frac{7}{3}$
B $\frac{1}{3}$
C $\frac{5}{3}$
D1
The area bounded by the curves $y = x^{2} and y = 2 - x^{2}$ is
A $\frac{8}{3}$ sq units
B $3 / 8$ sq units
C $3 \frac{/}{2}$ sq units
DNone of these