Let C be the circle of radius unity centred at the origin. If two positive numbers x1andx2 are such that the line passing through (x1,−1)and(x2,1) is tangent to C then x1⋅x2
x1x2=1
x1x2=−1
x1+x2=1
4x1x2=1
The correct Answer is:A
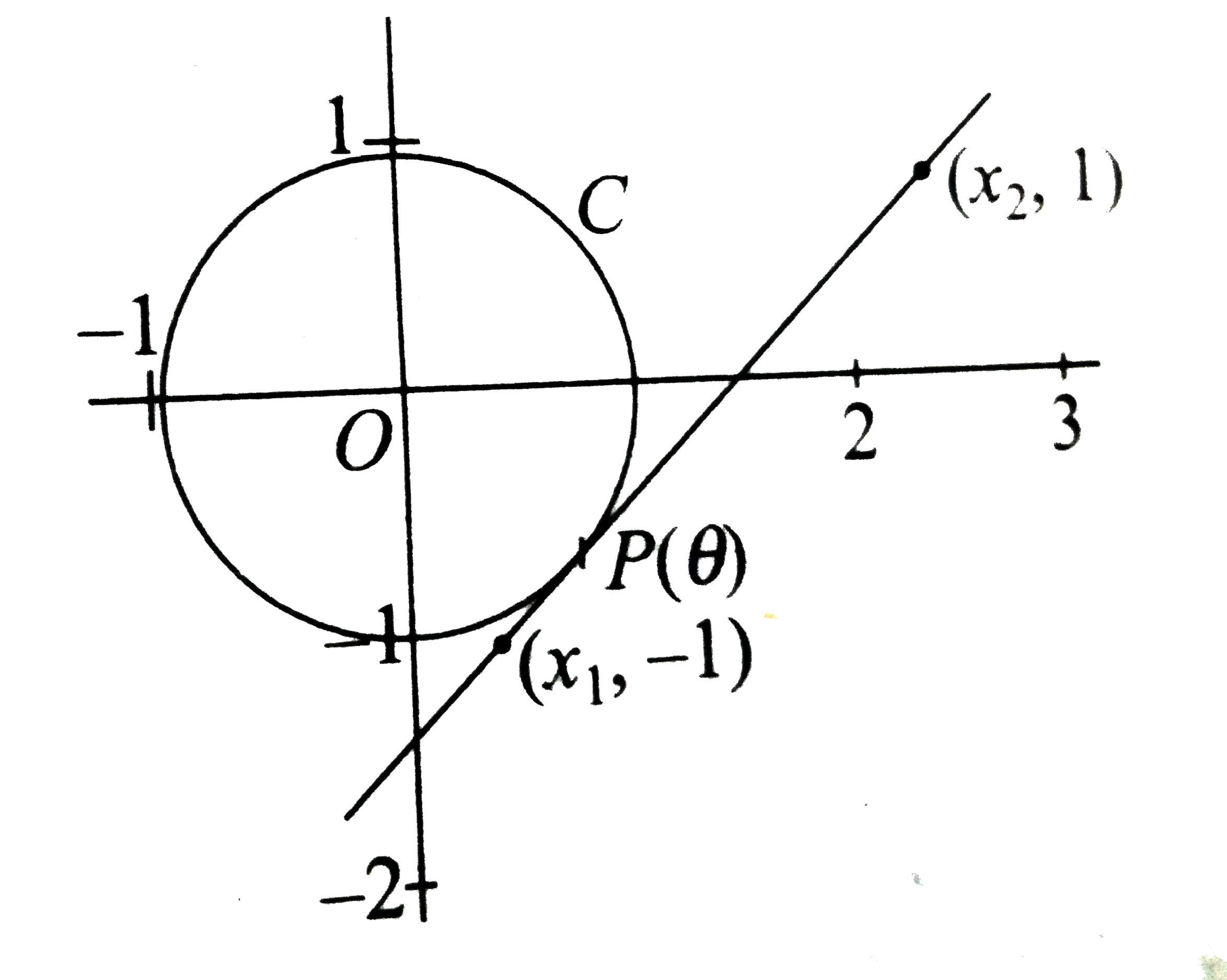
Equation of circle is x2+y2=1
The equation of tangent to circle at any point (cosθ,sinθ) is xcosθ+ysinθ=1.
Since it is passing through points (x1,−1) and (x2,1) we have
x1cosθ−sinθ=1 or x1cosθ=1+sinθ (i)
and x2cosθ=1−sinθ (ii)
Multiplying the results, we have
x1x2cos2θ=1−sin2θ
⇒x1x2cos2θ=cos2θ
⇒x1x2=1
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - JEE Advanced (Single Correct Answer Type)
14 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Question Bank
30 Videos
Similar Questions
Knowledge Check
Equation of the circle , centred at the origin , whose radius equals the distance between the lines x = -1 and x = 1 , is
Ax2+y2=1Bx2+y2=2Cx2+y2=4Dx2+y2=−4A circle passes through a fixed point A and cuts two perpendicular straight lines through A in B and C. If the straight line BC passes through a fixed-point (x1,y1), the locus of the centre of the circle, is
Ax1x+y1y=1Bx1y=x1y1Cxy1+yx1=2Dx1x+y1y=2Joint equation of lines passing through the origin, and parallel to the lines y−m1x+c1 and y=m1x+c2, is
Am1m2x2−(m1_m2)xy+y2=0Bm1m2x2+(m1+m2)xy+y2=0Cm1m2y2−(m1+m2)xy+x2=0Dm1m2y2+(m1+m2)xy+x2=0
A curve C passes through origin and has the property that at each point (x,y) on it the normal line at that point passes through (1,0). The equation of a common tangent to the curve C and the parabola y2=4x is
View SolutionLet C be the circle with centre at (1, 1) and radius = 1. If T is the circle centred at (0, y), passing through origin and touching the circle C externally, then the radius of T is equal to (1) √3√2 (2) √32 (3) 12 (3) 14
View SolutionThe centre of a circle is (2x−1,3x++1) and radius is 10 units. Find the value of x if the circle passes through the point (−3,−1).
View SolutionA circle with its centre on the line y=x+1 is drawn to pass through the origin and touch the line y=x+2 .The centre of the circle is
View SolutionFind the equation of the circle passing through the points (1,−1) and centre at the intersection of the lines x−y=4and2x+3y=−7
View Solution
