Let C be the circle with centre at (1, 1) and radius = 1. If T is the circle centred at (0, y), passing through origin and touching the circle C externally, then the radius of T is equal to (1) √3√2 (2) √32 (3) 12 (3) 14
√3√2
√32
12
14
The correct Answer is:4
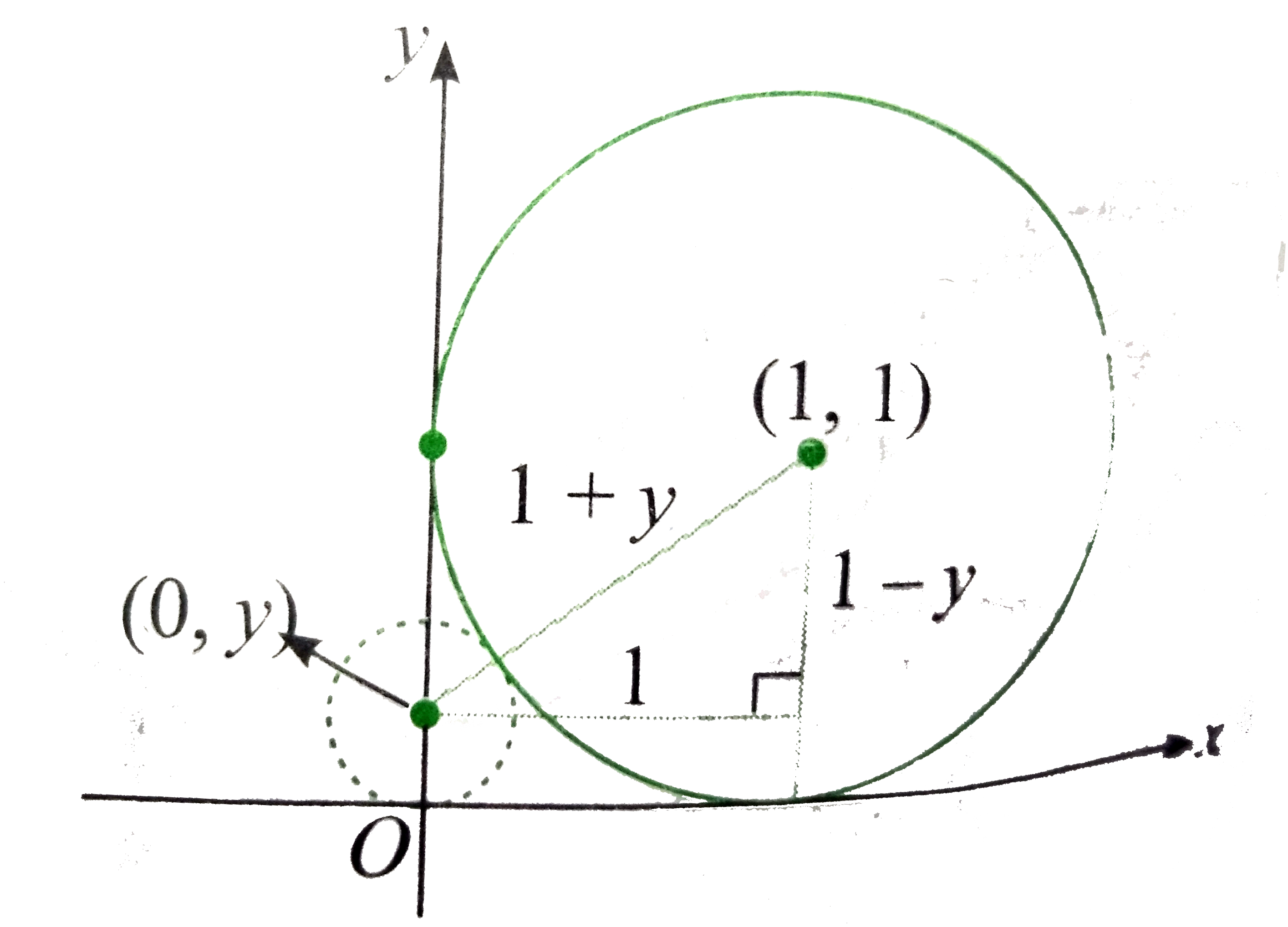
According to the figure,
(1+y)2+(1−y)2+1(y>0)
⇒y=14
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - JEE ADVANCED (Single Correct Answer Type)
3 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - LINKED COMPREHENSION TYPE (For problem 1 and 2)
2 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - ARCHIVES (JEE MAIN)
1 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
Let C be the circle with centre at (1, 1) and radius 1 If Tis the circle centred at (0, y), passing through origin and touching the circle C externally, then the radius of T is equal to V3 (a) 4
View SolutionLet C be the circle with centre at (1, 1) and radius = 1. If T is the circle centred at (0, y), passing through origin and touching the circle C externally, then the radius of T is equal to (1) √3√2 (2) √32 (3) 12 (3) 14
View Solution
Knowledge Check
Let C be the circle with centre (1,1) and radius 1 . If T is the circle centred at (0,y) , passing through origin and touching the circle C externally , then the radius of T is equal to
A12B14C√3√2D√32
Let C be the circle with centre (1,1) and radius 1.If T is the circle centered at (0,k) passing through origin and touching the circle C externally then the radius of T is equal to (a) √3√2 (b) √32 (c) 12 (d) 14
View Solution1) 1/5 2) 10 3) 10v2 4) 5v2 Let C be the circle with centre at (1,1) and radius -1. If T is the circle centered at (0,y), passing through origin and touching the circle C externally, then the radius of T is equal to 56. 3 2 1) 2) 3) 4)
View SolutionThe circle with centre (32,12) and radius √32 is
View SolutionFind the equation of the circle with centre : (1, 1) and radius √2
View SolutionFind the equation of the circle with centre(-1,-3) and radius √3
View SolutionIf the radius of the circle passing through the origin and touching the line x+y=2 at (1,1) is r units, then the value of 3√2r is
View SolutionFind the equation of the circle with : Centre(1,1)andradius√2.
View Solution
