Let f:R→R be a function defined by f(x)=∣x] for all x∈R and let A=[0,1), then f−1(A) equals
A
(-1,1)
B
(0,1)
C
(-1,0)
D
None of these
Video Solution
Text Solution
The correct Answer is:A
We have
f−1(A)=(x∈R:f(x)∈A)
Now,
f(x)∈A
⇒0<f(x)<1
⇒0<|x|<1⇒1<x<1⇒x∈(−1,1)
∴f−1(A)=(−1,1)
Alter: Clearly, f−1(A) denotes all points on x-axis whose images (y-coordinates) are between 0 and 1.
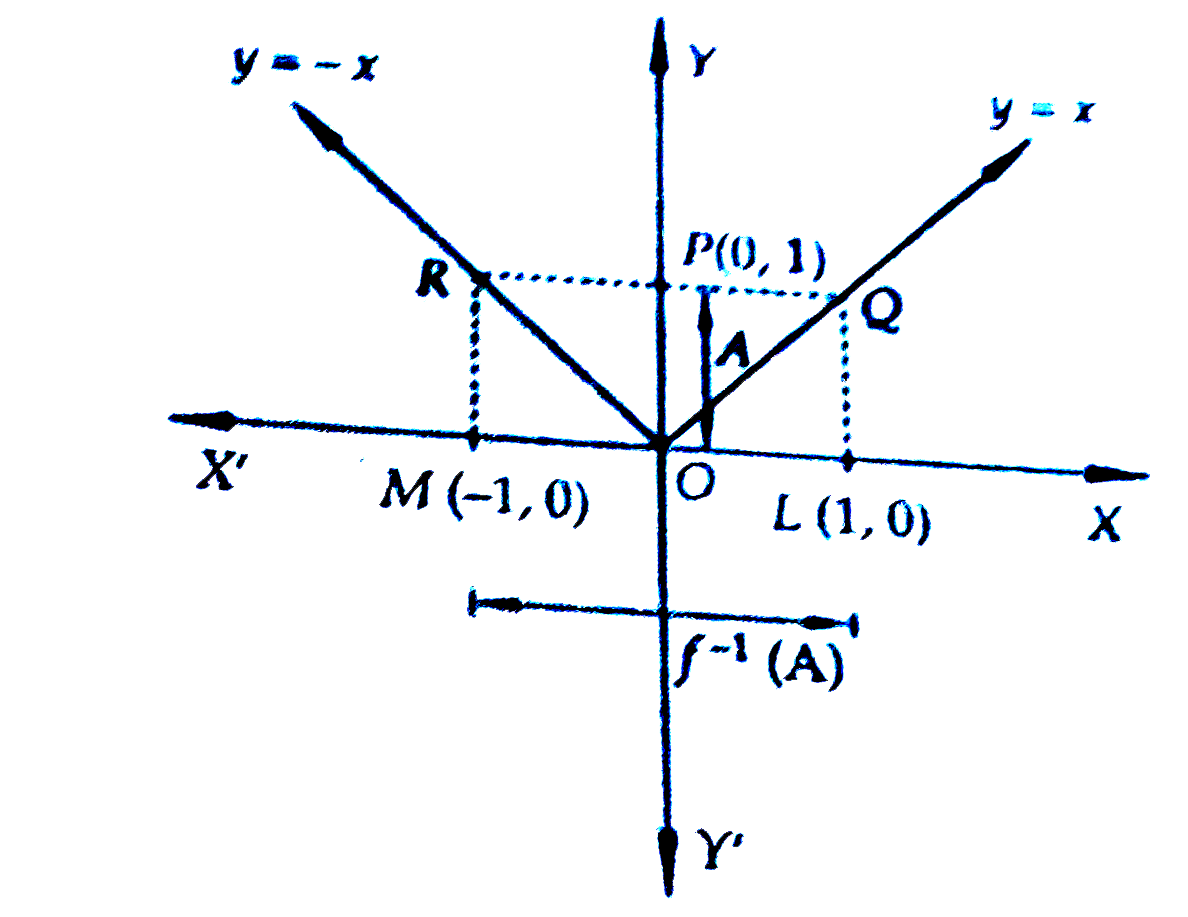
∴f−1(A)=(−1,1)
|
Topper's Solved these Questions
- FUNCTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - FUNCTIONSEXERCISE - Section II - Assertion Reason Type
10 Videos
- FUNCTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - FUNCTIONSEXERCISE - Exercise
48 Videos
- FUNCTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - FUNCTIONSEXERCISE - Chapter Test
30 Videos
- DISCRETE PROBABILITY DISTRIBUTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Exercise
40 Videos
- HYPERBOLABOOK - OBJECTIVE RD SHARMACHAPTER - HYPERBOLAEXERCISE - Chapter Test
29 Videos
Similar Questions
Knowledge Check
Let f:R→R be a function defined b f(x)=cos(5x+2). Then,f is
AinjectiveBsurjectiveCbijectiveDnone of theseLet f:R→R be function such that |f(x)|≤x2 for all x∈R. Than at x = 0, f is
Acontinuous but not differentiableBcontinuous as well as differentiableCneither continuous nor differentiableDdifferentiable but not continuousLet f:R→R be any function. Define g: R→R by g(x)=|f(x)| for all x. Then g is
Ag may be bounded even if f is unboundedBone-one if f is oneCcontinuous if f is continousDdifferentiable if f is differentiable
Let f:R→R be the function defined by f(x)=4x−3 for all x∈R. Then write f−1.
View SolutionLet f:R→R be the function defined by f(x)=2x−3,∀x∈R. Write f−1.
View SolutionLet f:R→R be a function defined by f(x)=x+√x2, then f is
View SolutionLet f : R → R be a function defined by f ( x ) = 4 x − 3 ∀ x ∈ R . Then Write f−1.
View SolutionLet f : R → R be a function defined by f ( x ) = 2 x − 5 ∀ x ∈ R . Then Write f−1.
View Solution
