Let f:R→R be a continuous onto function satisfying f(x)+f(−x)=0∀x∈R. If f(−3)=2andf(5)=4∈[−5,5], then the minimum number of roots of the equation f(x)=0 is
The correct Answer is:3
f(x)+f(−x)=0
Therefore,f(x) is an odd function.
Since points (-3, 2) and (5, 4) lie on the curve,
∴ (3, -2) and (-5, -4) will also lie on the curve.
For minimum number of roots, graph of continuous function f(x) is as follows:
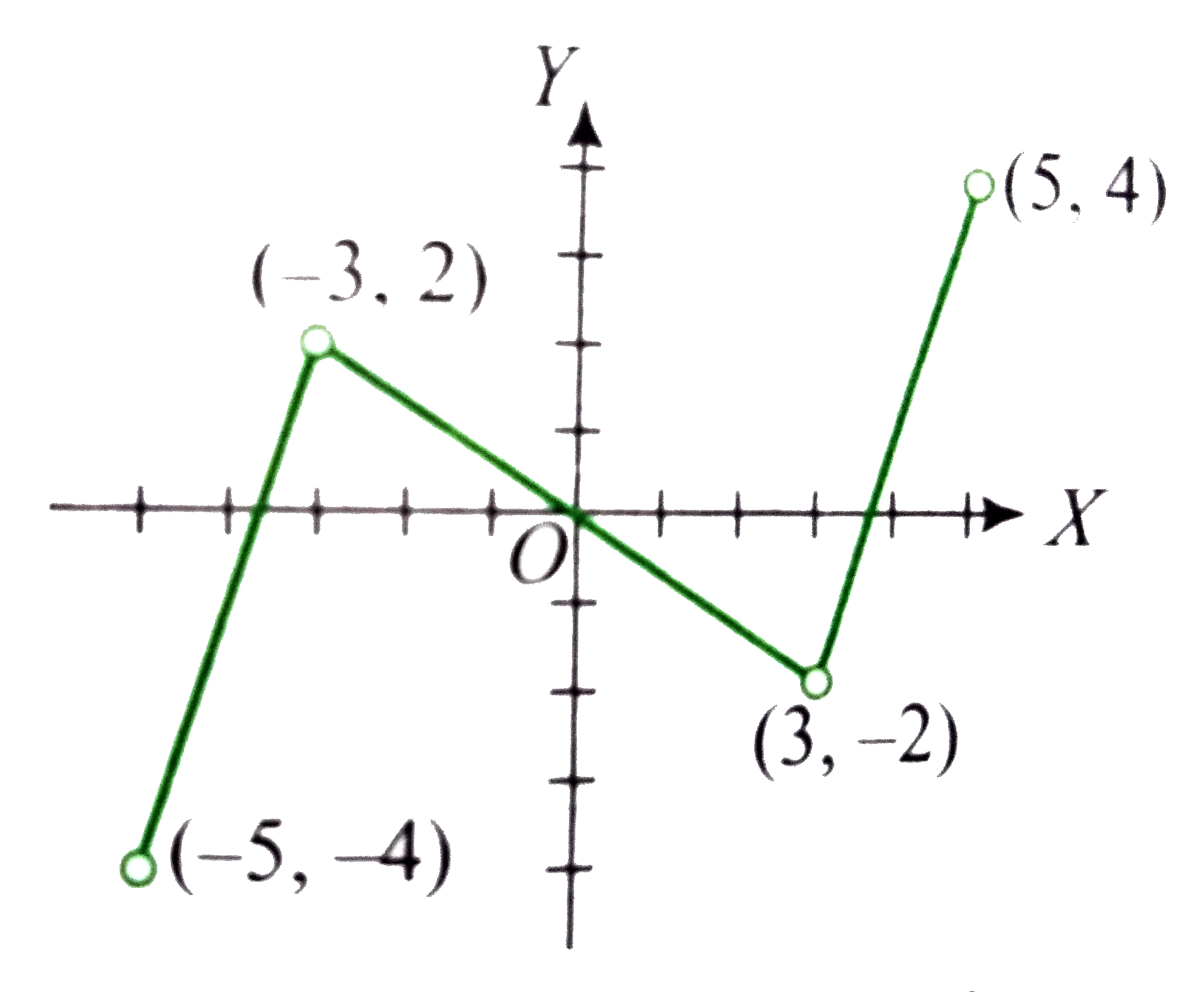
From the above graph of f(x), it is clear that equation f(x)=0 has at least three real roots.
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - JEE Previous Year
12 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Solved Examples And Exercises
498 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Matrix)
9 Videos
- Quadratic Equations, Inequalities, Modulus and LogarithmsBOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank
31 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
Let f:R→R be a continuous onto function satisfying f(x)+f(−x)=0∀x∈R. If f(−3)=2andf(5)=4∈[−5,5], then the minimum number of roots of the equation f(x)=0 is
View SolutionLet f:R→R be a continuous onto function satisfying f(x)+f(−x)=0,∀x∈R . If f(−3)=2andf(5)=4 in [-5, 5], then what is the minimum number of roots of the equation f(x) = 0?
View Solution
Knowledge Check
Let f be a differentiable function satisfying f'(x)=2f(x)+10∀x∈Randf(0)=0, then the number of real roots of the equation f(x)+5sec2x=0 ln (0,2π) is:
A0B1C2D3Let f be a continuous function satisfying f(x+y)=f(x)+f(y) for all x,y ∈ R and f(1)=5 then limx→4 f(x) is equal to
A4B80C0Dnone of these
Let f:R→R be a continuous onto function satisfying f(x)+f(−x)=0∀x∈R,. If f(−3)=2 and f(5)=4 in [−5,5] , then the equation f(x)=0 has
View SolutionLet f be a continuous function satisfying f'(Inx)=[1 for 0<x≤1,x for x>1 and f(0)=0 then f(x) can be defined as
View SolutionLet f(x) be a continuous & differentiable function on R satisfying f(−x)=f(x)&f(3+x)=f(3−x)∀x∈R. If f'(1)=−5 then f'(7) =
View SolutionLet f be a continuous function satisfying f(x) f(y)=f(x)+f(y)+f(xy)-2 for all x,y ∈ R and f(2)=5 then limx→4f(x) is
View SolutionLet f(x) is a continuous function such that f(−1)=−2,f(0)=−1,f(1)=0,f(2)=1,f(3)=0,f(4)=−1andf(5)=1 then minimum number of roots of f'(x)+xf(x)=0 in the interval (−1,5) are
View SolutionThere exists a function f(x) satisfying f (0)=1,f'(0)=-1,f(x) lt 0 ,AA x and
View Solution
