Let f:[0,4π]−−→0,π be defined by f(x)=cos−1(cosx). The number of points x∈[0,4π]satiy∈>he equation f(x)=10−x10 is____Solution in Bengali
The correct Answer is:3
f:[0,4π]→[0,π],f(x)=cos−1(cosx)
For number of roots of equation cos−1(cosx)=10−x10, draw the graph of y=cos−1(cosx)
and y=10−x10 and find the points of intersection.
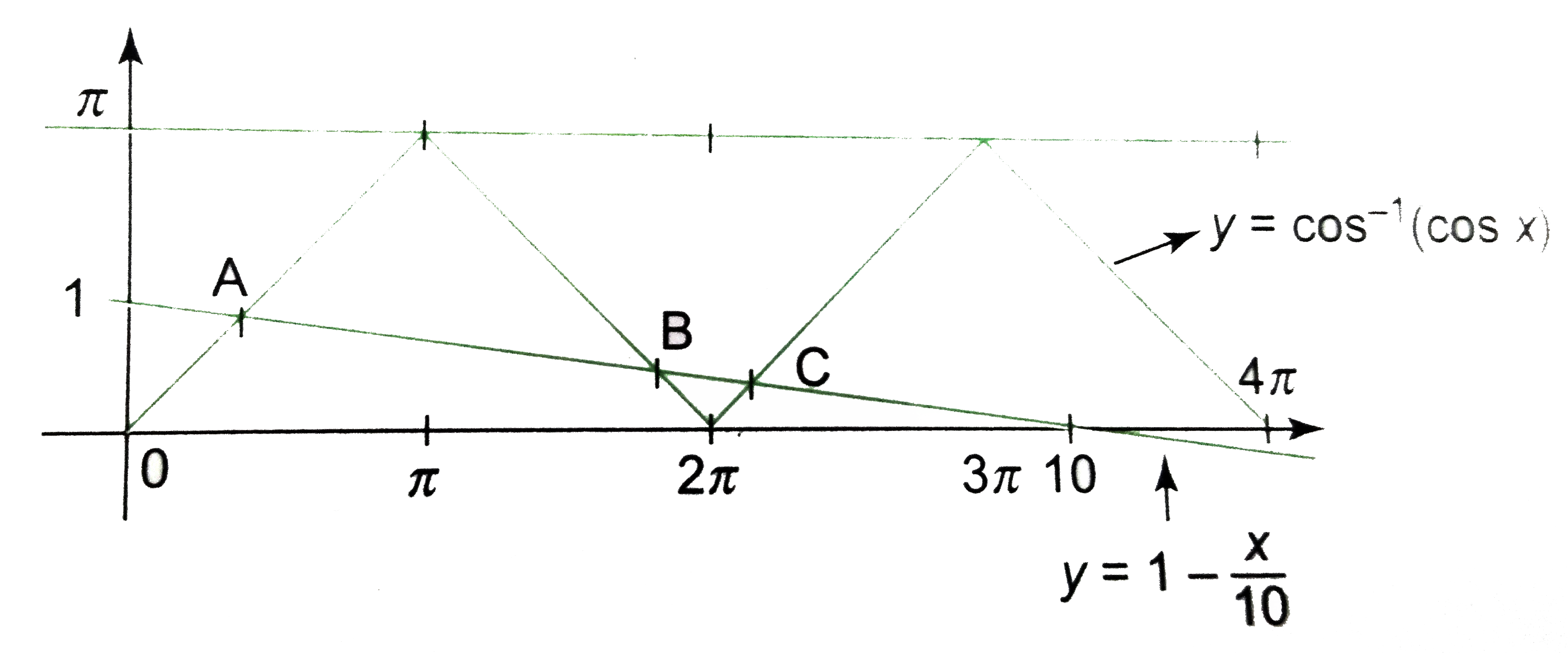
From the graph number of solution is 3
Topper's Solved these Questions
Similar Questions
The points with position vectors →x+→y,→x−→yand→x+λ→y are collinear for all real values of λ.
View SolutionIf y = y(x) is the solution of the differential equation, xdydx+2y=x2 satisfying y(1) = 1, then y(12) is equal to
View SolutionLet f:[0,4 pi]rarr[0,pi] be defined by f(x)=cos^(-1)(cos x). The number of points x in[0,4 pi]4 satisfying the equation f(x)=(10-x)/(10) is
View SolutionLet y=f(x) satisfies the equation
f(x)=(e−x+ex)cosx−2x+∫x0(x−t)f′(t)dt
The value of f(0)+f′(0) equal
View SolutionLet y=f(x) satisfies the equation f(x)=(e−x+ex)cosx−2x−∫x0(x−t)f'(t)dt. The value of f'(0)+f''(0)equals to
View SolutionThe number of points of discontinuity for f(x) sgn=(sin x), x∈[0,4π] is ___________.
View SolutionLet, f:[0,4π]→[0,π] be defined by f(x)=cos−1(cosx). The number of points x∈[0,4π] satisfying the equation
f(x)=10−x10
View SolutionLet f:[0,4π]→[0,π] be defined by f(x)=cos−1(cosx) then number of solution of equation 10(1−f(x))=x when x∈[0,4π] are
View Solutionमाना f:[0,4π]→[0,π],f(x)=cos−1(cosx) के द्वारा परिभाषित है। तब x∈[0,4π] में समीकरण f(x)=10−x10 को संतुष्ट करने वाले बिंदुओं की संख्या है
View SolutionLet f:[0,4π]→[0,π] be defined by f(x)=cos−1(cosx). The number of points x∈[0,4π] 4satisfying the equation f(x)=10−x10 is
View SolutionLet f:[0,4π]→[0,π] be defined by f(x)=cos−1(cosx). The number of points x∈[0,4π] 4satisfying the equation f(x)=10−x10 is
View SolutionLet f:[0,4π]→[0,π] be defined by f(x)=cos−1(cosx). The number of points x∈[0,4π] 4satisfying the equation f(x)=10−x10 is
View SolutionLet a function f(x)satiiex+f(2x)+f(2−x)+f(1+x)=∀x∈R. Then find the value of f(0).
View SolutionThe number of points of discontinuity for f(x) = sgn(sin x), x∈[0,4π] is ___________.
View Solutionagreed f:[0,4pi]to[0,pi],f(x)=cos^(-1)(cosx) Is defined by. Then x epsilon [0,4pi] Equation in f(x)=(10-x)/10 Is the number of points satisfying
View SolutionLet f:[0,4π]→[0,π] be defined by f(x)=cos−1(cosx). The number of points x∈[0,4π] satisfying the equation f(x)=10−x10 is
View Solution
