Let f,g:[−1,2]→R be continuous functions which are twice differentiable on the interval (−1,2). Let the values of fandg at the points −1,0and2 be as given in the following table: , x=−1 , x=0 , x=2 f(x) , 3, 6, 0 g(x) , 0, 1, −1 In each of the intervals (−1,0)and(0,2) the function (f−3g)'' never vanishes. Then the correct statement(s) is (are) f′(x)−3g′(x)=0 has exactly three solutions in (−1,0)∪(0,2). f′(x)−3g′(x)=0 has exactly one solutions in (−1,0). f′(x)−3g′(x)=0 has exactly one solutions in (−1,2). f′(x)−3g′(x)=0 has exactly two solutions in (−1,0) and exactly two solutions in (0,2).
f'(x)−3g,(x)=0 has exctly three solution in (−1,0)∪(0,2)
f(x)−3g'(x)=0 has exactly one solution in (-1,0)
f'(x)-3g'(x)=0 has exactly one solution in (0,2)
f'(x)-3g'(x)=0 has exactly one solution in (-1,0) and exactly one solution in (0,2)
The correct Answer is:D
Let F(x)=f(x)−3g(x)for all x∈[−1,2] We have,
F(−1)=f(−1)−3g(−1)=3−3×0=3
F(0)=f(0)−3g(0)=6−3×1=3
F(2)=f(2)−3g(2)=0−3×(−1)=3
By Rolle's theorem, F'(x) vanishes at least once in each of the interva [-1,0] and [0,2]
Now, F,(x)=f(x)=−3g(x)
⇒F'(x)=f''(x)−3g''(x)=(f''−3g'')(x)=(f−3g)''(x)
It is given that (f−3g)''(x)i.e.,F''(x) never vanishes. Therefore, F''(x)>0or,F''(x)<0for allx∈(−1,0)∪(0,2)
⇒F'(x) is either increasing or decreasing in (-1,0( and (0,2) .
⇒F'(x) 0 has exactly on solution in (-1,0) and one solution in (0,2)
⇒f'(x)−3g(x)=0 has exctly one solution in (-1,0)n adn exactly one solution in (0,2)
Topper's Solved these Questions
- MEAN VALUE THEOREMSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MEAN VALUE THEOREMSEXERCISE - Section II - Assertion Reason Type
4 Videos
- MEAN VALUE THEOREMSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MEAN VALUE THEOREMSEXERCISE - Exercise
28 Videos
- MEAN VALUE THEOREMSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MEAN VALUE THEOREMSEXERCISE - Exercise
28 Videos
- MATRICESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATRICESEXERCISE - Chapter Test
30 Videos
- PAIR OF STRAIGHT LINESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Chapter Test
18 Videos
Similar Questions
Let f,g:[−1,2]→R be continuous functions which are twice differentiable on the interval (-1, 2). Let the values of f and g at the points –1, 0 and 2 be as given in the following table : x=−1x=0x=2f(x)360g(x)01−1 In each of the intervals (-1,0) and (0, 2) the function (f – 3g)'' never vanishes. Then the correct statement(s) is(are)
View SolutionLet f,g:[−1,2]→ be continuous functions which are twice differentiable on the interval (-1,2). Let the values of f and g at the points and 2 be as given in the following table:
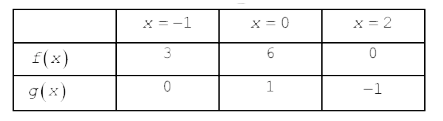
In each of the intervals (-1,0) and (0, 2) the function (f-3g) never vanishes. Then the correct statements(s) is(are) :
View SolutionLet f:R→ satisfying |f(x)|≤x2∀x∈R be differentiable at x=0. The find f′(0).
View SolutionLet f(x)andg(x) be differentiable functions such that f′(x)g(x)≠f(x)g′(x) for any real x. Show that between any two real solution of f(x)=0, there is at least one real solution of g(x)=0.
View SolutionIf f(a)=2,f′(a)=1,g(a)=−1,g′(a)=2, then the value of limx→ag(x)f(a)−g(a)f(x)x−a is (a)−5 (b) 15 (c) 5 (d) none of these
View SolutionIf f(x)=x+35x2+x−1 and g(x)=2x+3x220+2x−x2 such that f(x) and g(x) are differentiable functions in their domains, then which of the following is/are true (a) 2f′(2)+g′(1)=0 (b) 2f′(2)−g′(1)=0 (c) f′(1)+2g′(2)=0 (d) f′(1)−2g′(2)=0
View SolutionLet f(x)andg(x) be two differentiable functions in Randf(2)=8,g(2)=0,f(4)=10,andg(4)=8. Then prove that g′(x)=4f′(x) for at least one x∈(2,4).
View SolutionLet f(x)andg(x) be two differentiable functions in Randf(2)=8,g(2)=0,f(4)=10,andg(4)=8. Then prove that g′(x)=4f′(x) for at least one x∈(2,4).
View SolutionLet f(x)andg(x) be two functions which are defined and differentiable for all x≥x0. If f(x0)=g(x0)andf′(x)>g′(x) for all x>x0, then prove that f(x)>g(x) for all x>x0.
View SolutionLet f(x)andg(x) be two functions which are defined and differentiable for all x≥x0. If f(x0)=g(x0)andf′(x)>g′(x) for all x>x0, then prove that f(x)>g(x) for all x>x0.
View Solution
