Let f:R→R be a differentiable function such that f(x)=x2+∫x0e−tf(x−t)dt.
y=f(x) is
The curve y=f(x) passes through the point (1,2)
The curve y=f(x) passes through the point (2,-1)
The area of the region {(x,y)∈[0,1]×R:f(x)≤y≤√1−x2} is π−24
The area of the region {(x,y)∈[0,1]×R:f(x)≤y≤√1−x2} is π−14
The correct Answer is:B, C
f(x)=1−2x+x∫0ex−1f(t)dt
⇒ f(x)=1−2x+exx∫0e−tf(t)dt ...(i)
Differentiating w.r.t. x, we get
f'(x)=−2+exe−xf(x)+exx∫0e−tf(t)dt ...(ii)
Subtracting (i) from (ii), we get
f'(x)−f(x)=−2+f(x)−1+2x
⇒ f'(x)−2f(x)=2x−3
This is linear differential equation.
I.F.=e∫−2dx=e−2x
Therefore, solution is
y⋅e−2x=∫(2x−3)e−2xdx+c
⇒ y⋅e−2x=(2x−3)⋅e−2x−2−∫2×e−2x−2dx+c
⇒ y⋅e−2x=−(2x−3)e−2x2−e−2x2+c
⇒ y⋅e−2x=(1−x)e−2x+c
⇒ y=(1−x)+c.e2x ...(iii)
Putting x=0 in (i), we get f(0)=1.
So, from above equation, we have
1=1+c⇒c=0
Now, (iii) reduces to y=1-x, which passes through point (2,-1).
Now,f(x)≤y≤√1−x2
⇒ 1−x≤y≤√1−x2
1−x≤y represents the region above the line 1−x=yandy≤√1−x2 represents the region inside the semicircle (lying above x-axis) x2+y2=1.
So, common region is as the shaded one in the following figure :
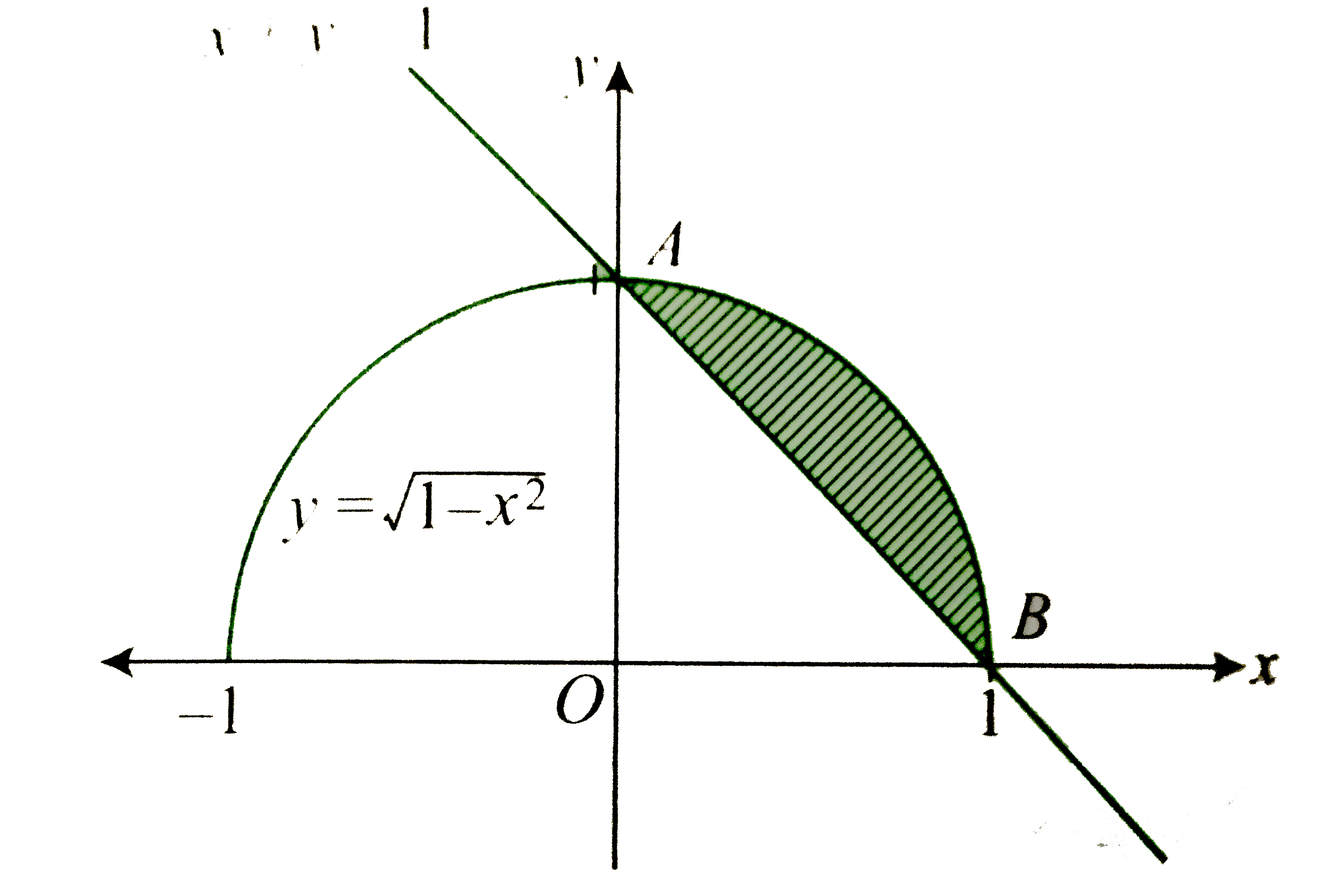
Area of the shaded region
=Area of quarter of the circle - Area of triangle OAB
=14×π(1)2−12×1×1=π−24
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Linkded Comprehension Type21videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Matrix Match Type5videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Exercises - Single Correct Answer Type40videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type5videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix4videos
BINOMIAL THEOREM
Similar Questions
Let f:R→R be a differentiable function such that f(x)=x2+∫x0e−tf(x−t)dt. f(x) increases for
View SolutionLet f:R→R be a differntiable function satisfying f(x)=x2+3∫x0e−t3.f(x−t3)dt. Then find f(x).
View SolutionLet f(x) be a differentiable function such that f(x)=x2+∫x0e−tf(x−t)dt then ∫10f(x)dx=
View SolutionLet f be a differentiable function such that f'(x)=f(x)+∫20f(x)dxandf(0)=4−e23. Find f(x).
View SolutionLet f(x) be a differentiable function satisfying f(x)=∫x0e(2tx−t2)cos(x−t)dt, then find the value of f''(0).
View SolutionIf f(x) is a twice differentiable function such that f(0)=f(1)=f(2)=0. Then
View SolutionLet f(x)andg(x) be differentiable functions such that f(x)+∫x0g(t)dt=sinx(cosx−sinx)and(f'(x))2+(g(x))2=1,thenf(x)andg(x) respectively , can be
View SolutionLet f:(0,∞)→R be a continuous function such that f(x)=∫x0tf(t)dt. If f(x2)=x4+x5, then 12∑r=1f(r2), is equal to
View SolutionLet f be a differentiable function satisfying ∫f(x)0f−1(t)dt−∫x0(cost−f(t)dt=0 and f(π2)=2π
The value of limx→0cosxf(x) is equal to where [.] denotes greatest integer functionView SolutionLet f be a differentiable function satisfying ∫f(x)0f−1(t)dt−∫x0(cost−f(t)dt=0 and f(π2)=2π
The value of ∫π/20f(x)dx lies in the intervalView Solution

