Let f(x)={1−|x|,|x|≤10, |x|>1 and, g(x)=f(x-1)+f(x+1) for all x∈R. Then, the value of ∫3−3g(x)dx, is
A
2
B
3
C
4
D
5
Video Solution
Text Solution
The correct Answer is:A
The graph of f(x) and g(x) are shown in Fig. 14 and 15 respectively.
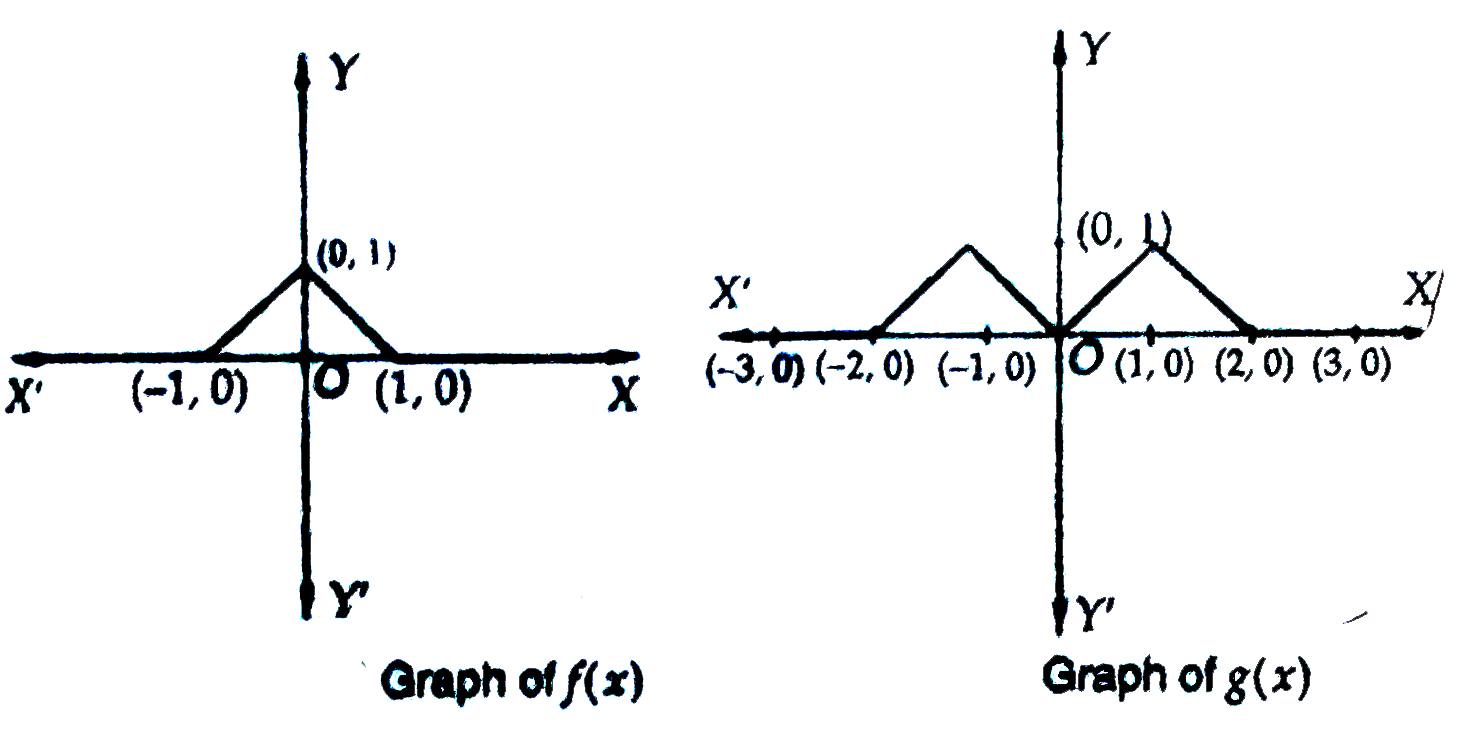
Clearly,
3∫−3g(x)dx=−2∫−30dx+0∫−2f(x)dx+2∫0f(x)dx+3∫20dx
⇒3∫−3g(x)dx=22∫0f(x)dx=2(12×2×1)=2
|
Topper's Solved these Questions
- DEFINITE INTEGRALSBOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Section II - Assertion Reason Type
12 Videos
- DEFINITE INTEGRALSBOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Exercise
147 Videos
- DEFINITE INTEGRALSBOOK - OBJECTIVE RD SHARMACHAPTER - DEFINITE INTEGRALSEXERCISE - Chapter Test 2
60 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - OBJECTIVE RD SHARMACHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise
86 Videos
- DERIVATIVE AS A RATE MEASURER BOOK - OBJECTIVE RD SHARMACHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Exercise
26 Videos
Similar Questions
Knowledge Check
Let f(x)={1−|x|,|x|≤10,|x|>1andg(x)=f(x−1)for allx∈R The graph for g(x) is given by
A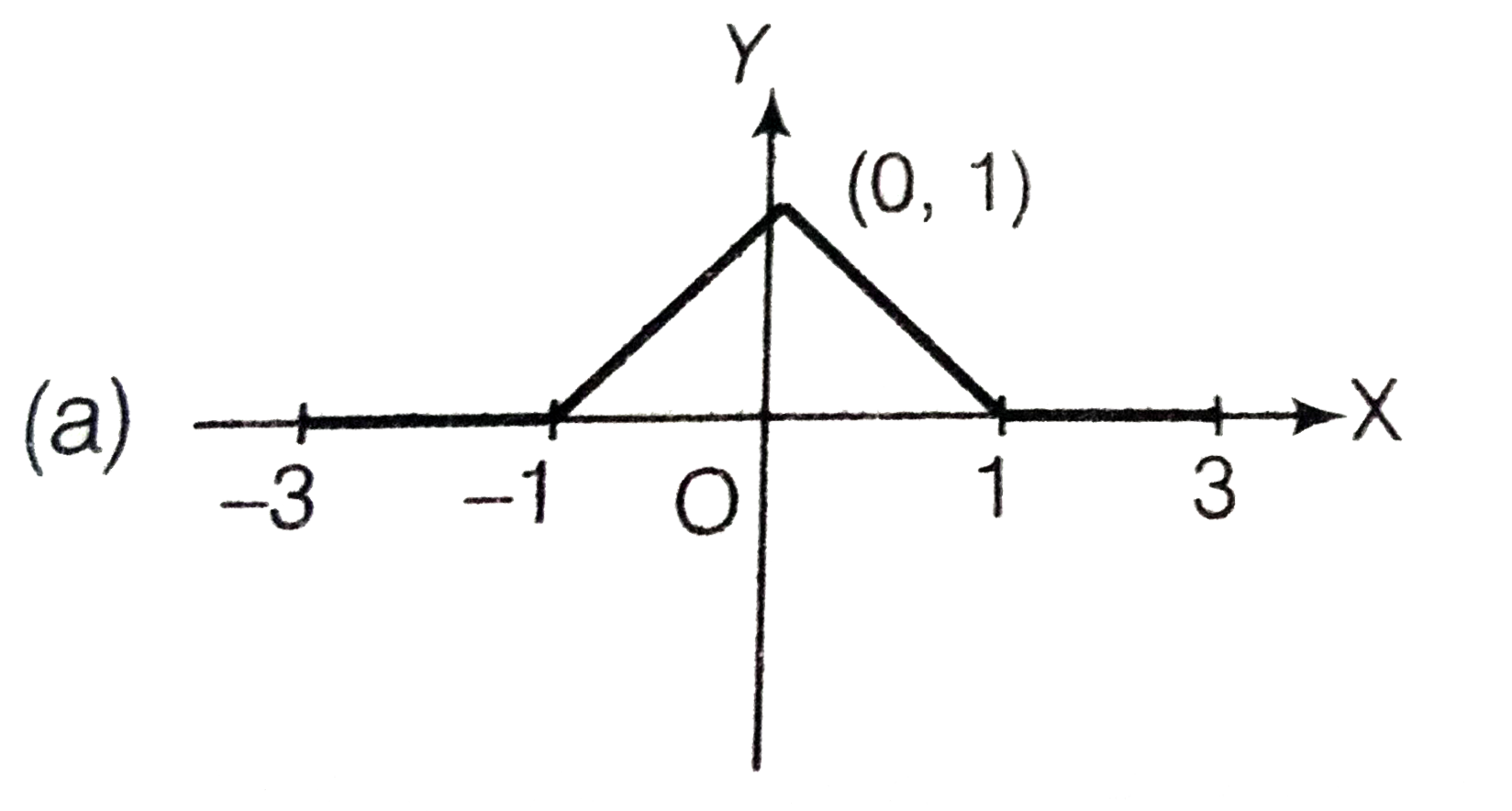 B
B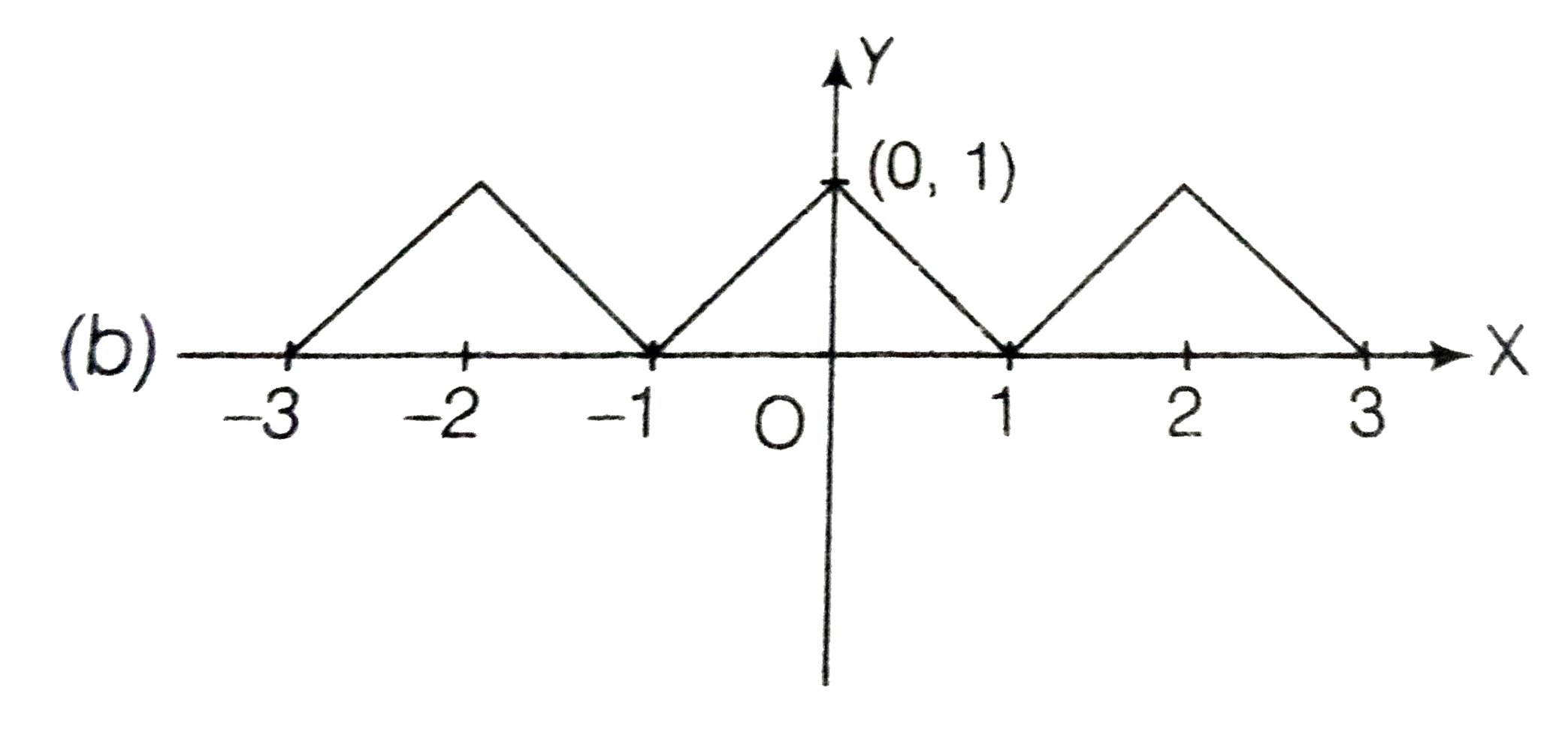 C
C D
D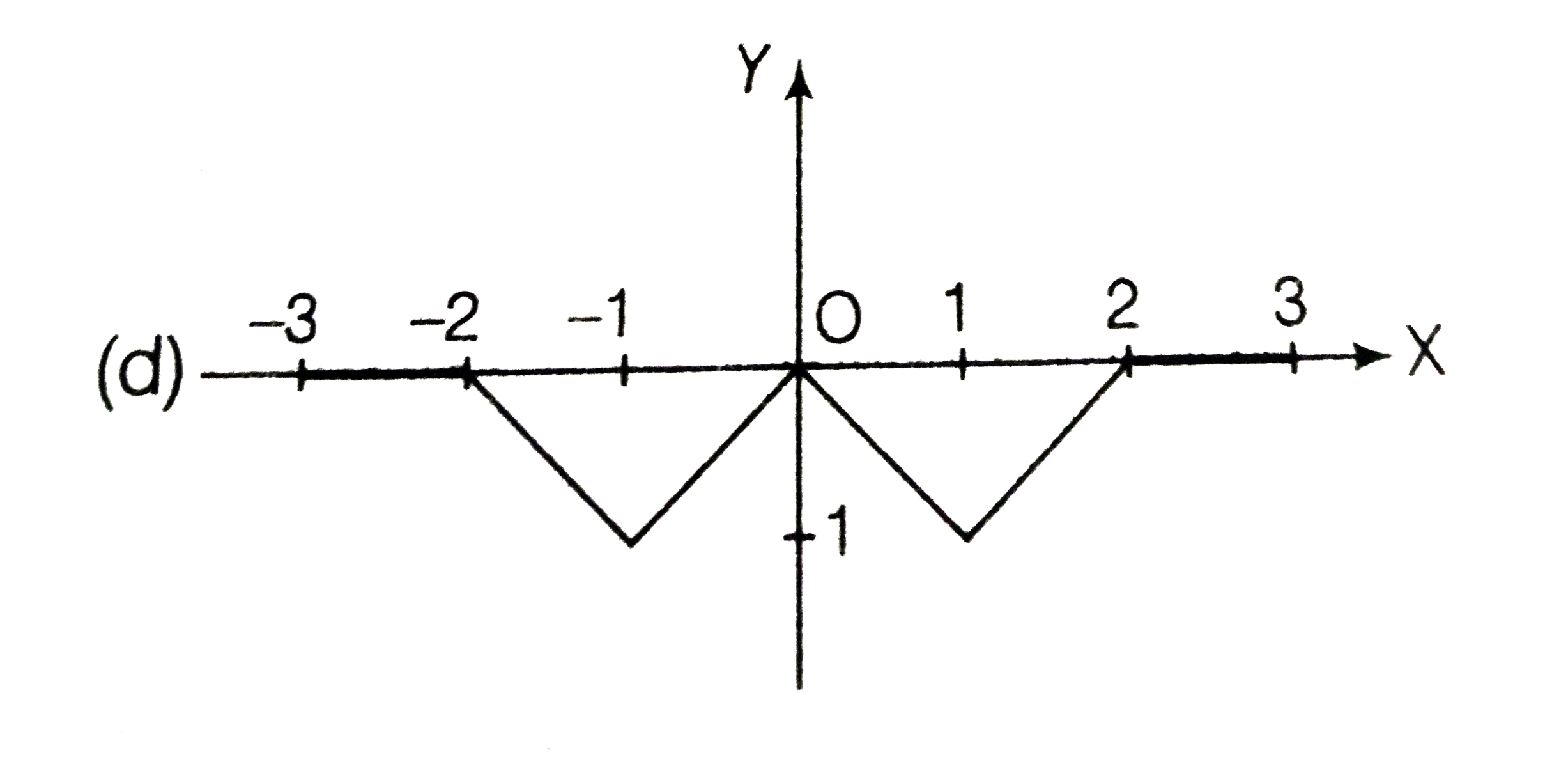
Let f:R→R be continuous function such that f(x)=f(2x) for all x∈R. If f(t)=3, then the value of ∫1−1f(f(x))dx, is
A3f(0)B0C3f(3)D6Let f(x)={−1,−2≤x<0x2−1,0≤x≤2 and g(x)=|f(x)|+f(|x|). Then in the interval (−2,2), g is
Adifferentiable at all pointsBnot differentiable at two pointsCnot continuousDnot differentiable at one point
Let f(x)=minimum {|x|,1−|x|,14} for xεR then the value of ∫1−1f(x)dx is equal to
View Solutionlet (f(x)=1−|x|,|x|≤1,0,|x|>1) g(x)=f(x+1)+f(x−1)
View SolutionIf f(x)=x(x−1),0≤x≤1,andf(x+1)=f(x)∀x∈R, then ∣∣∣∫42f(x)dx∣∣∣ is _____________
View Solutionf(x)={1−2x, for x≤01+2x, for x>0 then ∫1−1f(x)dx=
View SolutionLet f(x)= max {3,x2,1x2} for 12≤x≤2. Then the value of integral ∫21/2f(x)dx is
View Solution
