Let f(x),g(x),andh(x) be the quadratic polynomials having positive leading coefficients and real and distinct roots. I eco pair of them has a common roots, then fine the roots of f(x)+g(x)+h(x)=0.
Let f(x)=a1(x−α)(x−β),
g(x)=a2)x−β)(x−γ),
and h(x)=a3(x−γ)(x−α),
where a1,a2,a3 are positive.
Let f(x)+g(x)+h(x)=F(x)
⇒F(α)=a2(α−β)(α−γ)
F(β)=a3(β−γ)(β−α)
f(γ)=a1(γ−α)(γ−β)
⇒F(α)F(β)F(γ)=−a1a2a3(α−β)2(β−γ)2(γ−α)2<0
So, roots of F(x) = 0 are and distinct.
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - CONCEPT APPLICATION EXERCISE 2.1
3 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - CONCEPT APPLICATION EXERCISE 2.2
5 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - ILLUSTRATION
122 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
294 Videos
Similar Questions
Let f(x),g(x), and h(x) be the quadratic polynomials having positive leading coefficients and real and distinct roots. If each pair of them has a common root, then find the roots of f(x)+g(x)+h(x)=0.
View SolutionLetf(x)=x4+ax3+bx2+cx+d be a polynomial with real coefficients and real roots. If |f(i)|=1where i=√−1, then the value of a +b+c+d is
View SolutionLet f(x)=x2+ax+b, where a,b∈R. If f(x)=0 has all its roots imaginary, then the roots of f(x)+f'(x)+f''(x)=0 are
View SolutionLet f(x) be a quadratic polynomial satisfying f(2) + f(4) = 0.
If unity is one root of f(x) = 0 then find the other root.
View SolutionIf a quadratic polynomial f(x) is factorizable into linear distinct factors, then what is the total number of real and distinct zeros of f(x) ?
View SolutionLet f(x) be a polynomial with integral coefficients. If f(1) and f(2) both are odd integers, prove that f(x) = 0 can' t have any integral root.
View SolutionLet f(x)=x3+x+1, let p(x) be a cubic polynomial such that the roots of p(x)=0 are the squares of the roots of f(x)=0 , then
View SolutionConsider the following figure.
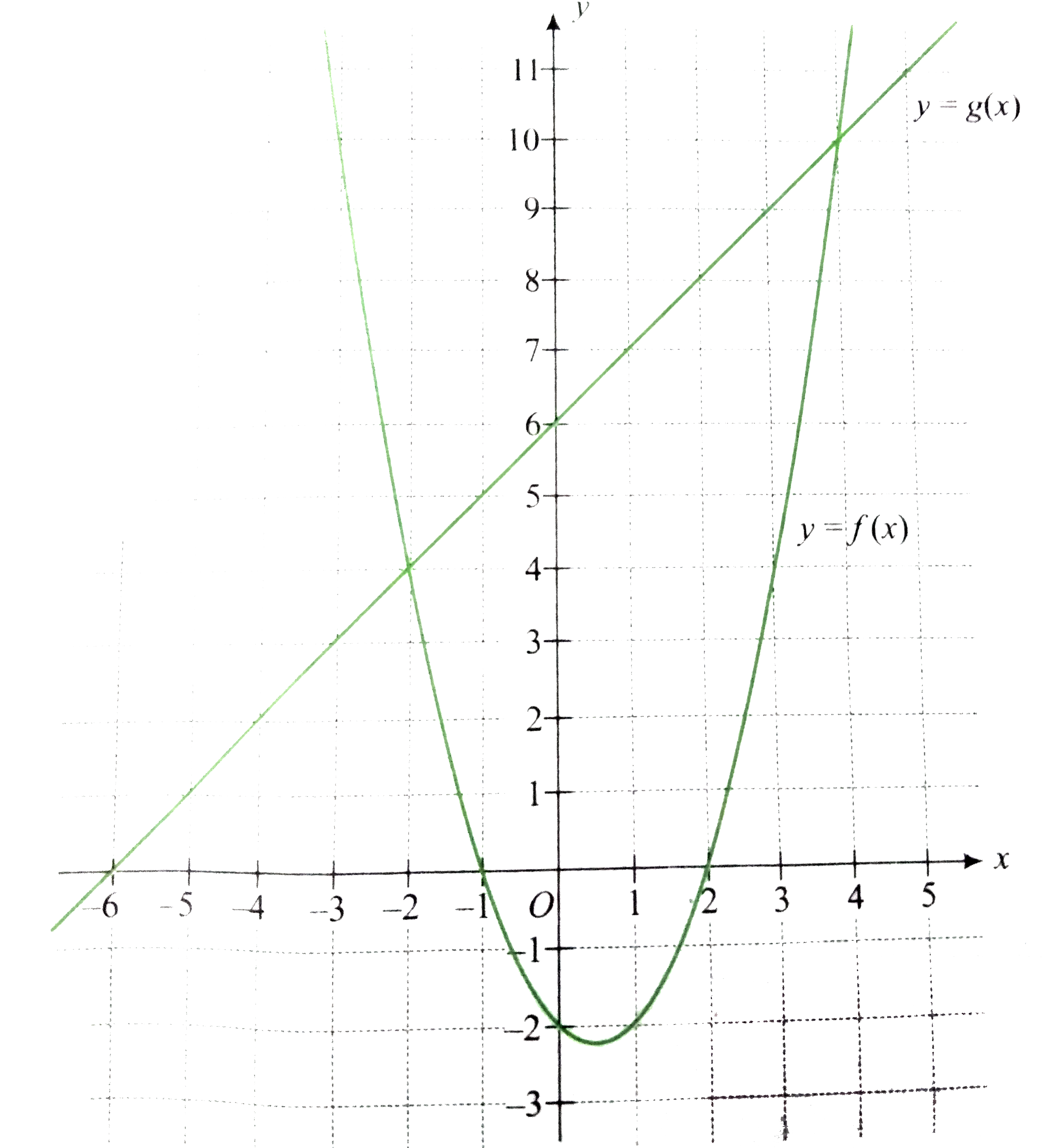
Answer the following questions
(i) What are the roots of the f(x) = 0?
(ii) What are the roots of the f(x) = 4?
(iii)What are the roots of the f(x) = g (x)?
View SolutionLet f(x) be a cubic polynomial with leading coefficient unity such that f(0)=1 and all the roots of f'(x)=0 are also roots of f(x)=0. If ∫f(x)dx=g(x)+C, where g(0)=14and C is constant of integration, then g(3)−g(1) is equal to
View SolutionIf the equaion x2+ax+b=0 has distinct real roots and x2+a|x|+b=0 has only one real root, then
View Solution
