Let f(x)=x3−9x2+24x+c=0 have three real and distinct roots α,β and λ.
(i) Find the possible values of c.
(ii) If [α]+[β]+[λ]=8, then find the values of c, where [⋅] represents the greatest integer function.
(ii) If [α]+[β]+[λ]=7, then find the values of c, where [⋅] represents the greatest integer functionsSolution in Bengali
We have y=f(x)=x3−9x2+24x+c
f'(x)=3x2−18x+24=3(x−2)(x−4)
Sign scheme of f'(x) is as follows.
x=4 is the point of local minima and x = 2 is the point of local maxima.
f(2)=20,f(4)=16
Ifc=0, then f(0)=0
So the graph of y=f(x) for c=0 can be draws as follows.
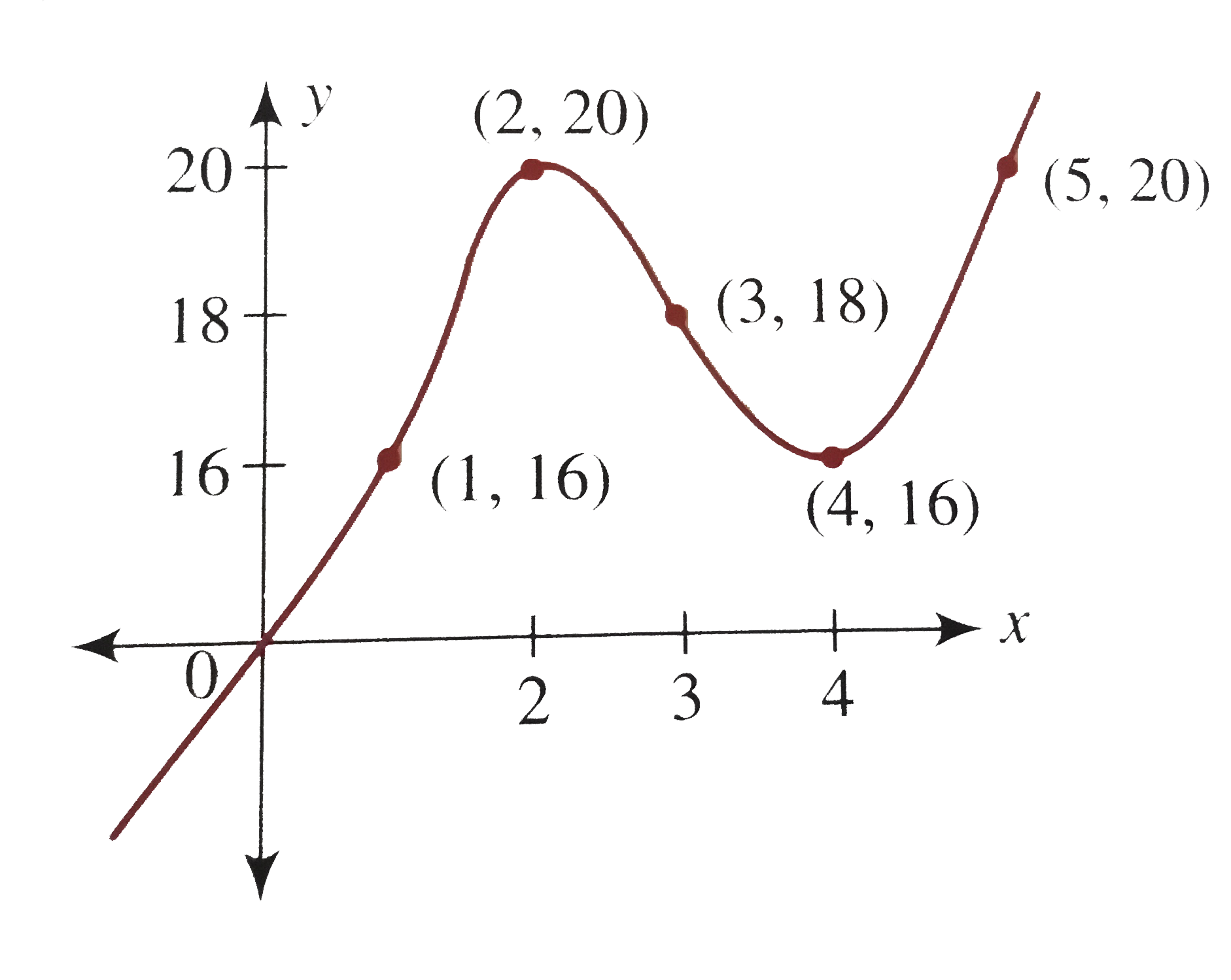
From the figure, for three real roots of f(x)=x3−9x2+24x+c=0, c must lie in the interval (−20,−16).
∴f(0)=c<0
f(1)=1−9+24+c=c+16<0,∀c∈(−20,−16)
f(2)=8−36+48+c=c+20>0,∀c∈(−20,−16)
∴α∈(1,2)⇒[α]=1
f(3)=27−81+72=18+c
⇒f(3)>0 if c∈(−20,−18) or f(3)<0 if c∈(−18,−16)
or β∈(2,3) if c∈(−18,−16)
and β∈(3,4) if c∈(−20,−18)
Now f(4)=64−144+96+c=16+c<0,∀c∈(−20,−16)
f(5)=125−225+120+c=c+20>0,∀c∈(−20,−16)
∴λ∈(4,5)⇒[λ]=4
Thus [α]+[β]+[λ]={1+3+4, −20<c<−181+2+4, −18<c<−16
Topper's Solved these Questions
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
17 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - ILLUSTRATION
78 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES
34 Videos
Similar Questions
Draw the graph of y=(x−1)(x2−x+1).
View SolutionPlot y=|x|,y+x−2∣,andy=|x|2∣
View SolutionDraw the graph of y=1(1/x).
View Solutionf(x)=x^(3)-9x^(2)+24x+c has real roots alpha,beta,gamma then find the value of [alpha]+[beta]+[gamma] Where [] represents greatest integer function
View SolutionIf the function f(x)=x3−9x2+24x+c has three real and distinct roots α,β and γ, then the value of [alpha]+[beta]+[gamma] is
View SolutionIf x3+3x2−9x+c=0 have roots α,αandβ then possible value of α+β is
View SolutionLet f(x)=x3−9x2+24x+c=0 have three real and distinct roots α,β and λ.
(i) Find the possible values of c.
(ii) If [α]+[β]+[λ]=8, then find the values of c, where [⋅] represents the greatest integer function.
(ii) If [α]+[β]+[λ]=7, then find the values of c, where [⋅] represents the greatest integer function.s
View SolutionIf [α]+[β]+[γ]=7 then the values of c, where [.] represent the greates integer function are,
View SolutionLet a, b, c ∈ R and α,β are the real roots of the equation ax2 + bx + c = 0 and if a + b + c < 0, a – b + c < 0 and c > 0 then [α]+[β] is equal to (where [.] denotes the greatest integer function.)
View SolutionLet a,b,cεR and α,β, are the real roots of the equation ax2+bx+c=0 and in a+b+c<0,a−b+c<0 andc>0 then [α]+[β] is equal to (where[.] denotes the greatest integer function).
View SolutionIf f(x)=0 is a cubic equation with positive and distinct roots α,β,γ such that β is H.M .of the roots of f'(x)=0 .If K=[2βα+γ] where [.] represents greatest integer function then find 5∑i=K(2)K
View SolutionLet α,β be the roots of x2+(3−λ)x−λ=0, then the value of λ for which α2+β2 is minimum, is-
View SolutionLet the roots f(x)=x be αandβ where f(x) is quadratic polynomial ax2+bx+c.αandβ are alos the roots of f(f(x))=x. Let the other two roots of f(f(x))=x be λ and δ.
If α+β+λ+δ, then the correct statements are
I : αandβ are real
II : λandδ are real
III αandβ are imaginary
IV : λandδ are imaginary
View SolutionIf the roots of the equation x2−bxax−c=λ−1λ+1 are such that α+β=0, then the value of λ is :
View SolutionIf roots α,β of the equation x2−bxax−c=λ−1λ+1 are such that α+β=0, then the value of λ is
View SolutionLet f(x)=x3−9x2+24x+c=0 have three real and distinct roots α,β and λ.
(i) Find the possible values of c.
(ii) If [α]+[β]+[λ]=8, then find the values of c, where [⋅] represents the greatest integer function.
(ii) If [α]+[β]+[λ]=7, then find the values of c, where [⋅] represents the greatest integer function.s
View Solution
