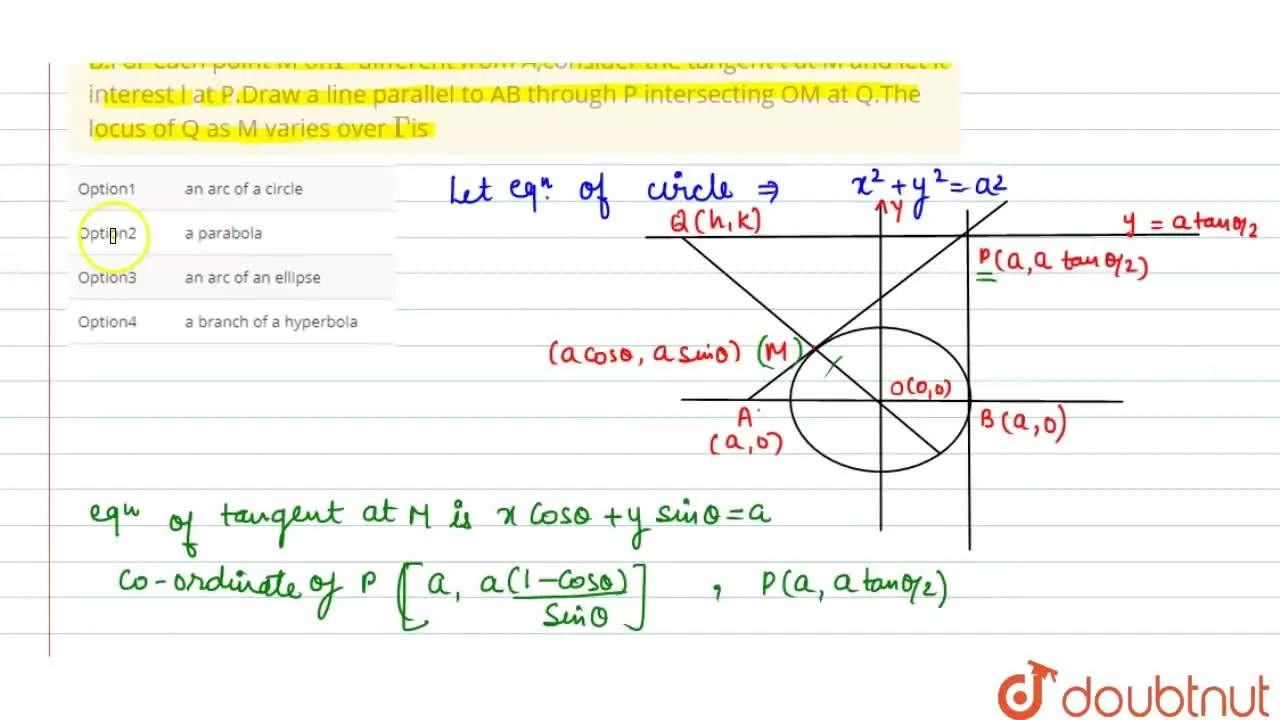
Let Γ be a circle with diameter AB and centre O.Let l be the tangent toΓ at B.For each point M onΓ different from A,consider the tangent t at M and let it interest l at P.Draw a line parallel to AB through P intersecting OM at Q.The locus of Q as M varies over Γis
an arc of a circle
a parabola
an arc of an ellipse
a branch of a hyperbola
The correct Answer is:B

Equation of tangent at M, xcosθ+ysinθ=r
put x=r, to get y-coordinate of point P.
rcosθ+ysinθ=r
⇒y=r(1−cosθ)sinθ=r.2.sin2θ22.sinθ2.cosθ2=rtanθ2
∴P=(r,rtanθ2)
∴ Q has y-coordinate same as point P
∴K=rtanθ2⇒tanθ2=Kr
Slope of tangent at M=−cotθ
Slope of OQ=Kh
∴Kh,(−cotθ)=−h⇒thanθ=Kh
⇒2tanθ21−tan2θ2=Kh⇒2.Kr1−K2r2=Kh
⇒2hr=1−K2r2⇒2hr=r2−K2r2
⇒2hr=r2−K2
⇒y2=r2−2Kr
y2=−2r(x−r/2)
∴ Parabola
Related Playlists
- BOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part 2 Mathematics15videos
KVPY
- BOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Matematics20videos
KVPY
- BOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-1 MATHEMATICS20videos
KVPY
- BOOK - KVPY PREVIOUS YEARCHAPTER - KVPY 2021EXERCISE - PART II MATHEMATICS4videos
KVPY 2021
Similar Questions
Let Γ be a circle with diameter AB and centre O.Let l be the tangent toΓ at B.For each point M onΓ different from A,consider the tangent t at M and let it interest l at P.Draw a line parallel to AB through P intersecting OM at Q.The locus of Q as M varies over Γis
View SolutionGiven a line l and a point M on it draw a perpendicular MP of l where MP=5.2cm and a line q parallel to l through P.
View SolutionThe tangents are drawn at the extremities of diameter AB of a circle with centre P. If a tangent to the circle at the point C Intersects the other two tangents at Q and R, then the measure of the ∠QPR is
View SolutionTP and TQ are tangents from T to the circle with centre O. Then is it possible to draw a circle through the points P, O, Q and T ?
 View Solution
View SolutionTangents are drawn at extremities AB of a diameter of a circle centred at P. If tangents drawn at a point C on the circle meet the other two tangents respectively at Q and R then measure of ∠QPR is
View SolutionIf the tangent at a point P to a circle with centre O cuts a line through O at Q such that PQ=24cm and OQ=25cm . Find the radius of the circle.
View SolutionLet P be a point on the circle S with both coordinates being positive. Let the tangent to S at P intersect the coordinate axes at the points M and N. Then, the mid-point of the line segment MN must lie on the curve.
View SolutionPQ is a chord of length 8 cm, of a circle with centre O and of radius 5 cm. The tangents at P and Q intersect at a point T. The length of TP is
View SolutionLet P and Q be 2 circles externally touhing each other at point X. Line segment AB is a direct common tangent to circle P and Q at points A and B respectively. Another common tangent to P and Q at X intersects line AB at a point Y. If BY = 10 units and the radius of P is 9 units, then the value of the reciprocal of the radius of the radius of the circle Q is equal to
View SolutionTwo different points P and Q are given on one side of line AB. Draw a circle passing through the points P and Q touching the line AB in point R.
View Solution